數學教學,需要慢的藝術
劉一萍

[摘 ?要] 教育是慢的藝術. 文章以“探索直角三角形全等的條件”的教學為例,探尋初中數學慢的教學藝術路徑,即創設情境,引入主題;合作交流,獲得新知;變式應用,拓展延伸,以拓展學生思維空間,發展學生數學能力,促進學生核心素養的生成.
[關鍵詞] 慢教育;藝術;初中數學
教育就是慢的藝術,所謂“慢”就是平靜和平和,就是細致和細膩,需要數學教師的耐心與耐性[1]. 數學本質的獲取需要經過內在加工與提煉的過程,需要緩慢的時間與一定空間. 因此,在慢教育的過程中,教師要引導學生經歷數學知識的形成發展過程,在知識的深度與廣度方面有所保障,才能拓展學生思維空間,發展學生數學能力,促進學生核心素養的生成. 筆者以“探索直角三角形全等條件”的教學為例,展現教育的慢理念.
創設情境,引入主題
師:關于判定兩個一般的三角形全等,我們已經學習了哪些方法?
生:判定兩個一般的三角形全等,我們已學習了四種方法,一是邊角邊,二是角邊角,三是角角邊,四是邊邊邊.
師:由此可見,要判定兩個三角形全等,至少需要三個條件,其中一個至少是邊相等.
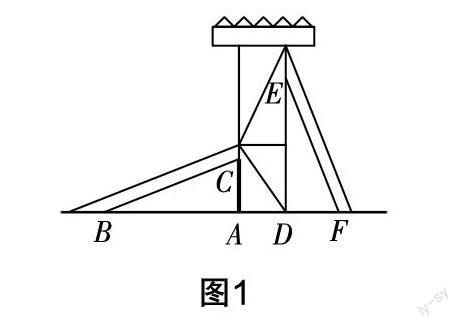
多媒體呈現:如圖1所示,新蕾幼兒園剛進了一個滑梯,左右兩個滑梯長度相等,左邊滑梯的高度與右邊滑梯水平長度相等. △ABC與△DEF全等嗎?兩個滑梯的傾斜角∠ABC與∠DFE有什么關系?
生:根據已知條件,可得在△ABC與△DEF中,只有兩組邊相等的條件,即BC=EF,AC=DF,而判定兩個三角形全等至少需要三個條件,因此,無法判定這兩個三角形全等.
生:還有一個隱含條件,即∠BAC=∠EDF=90°,但是這樣構成的全等條件是“邊邊角”,“邊邊角”不能判定兩個三角形全等.
師:兩位同學分析得很到位,根據目前的條件無法判定這兩個直角三角形全等,但是幼兒園的工作人員認為,這兩個三角形全等,你認可他們的結論嗎?
學生感到困惑……
設計意圖 ?引入生活模型,創設問題情境,讓學生慢慢地體悟與思考,對生活實際問題進行提煉,發展學生抽象數學模型的能力;學生是教學活動的主體,讓學生參與到新知識的獲取當中,發現生活實際與數學的關系,認識與領悟到學習數學的意義. 知識生長的過程被拉長,學生通過慢慢地領悟,實現了知識的銜接與生長,在慢思維的參與下,引出教學主題,即直角三角形全等的條件[2].
合作交流,獲得新知
師:請同學們嘗試畫出下面的圖形. (1)任意畫一個直角,∠QCP=90°;(2)在射線CP上截取一條長為2 cm的線段CB;(3)以點B為圓心,以4 cm的長為半徑畫弧,與射線CQ交于點A,連接AB. 大家嘗試把各自畫的圖疊合在一起,看是否能重合,能得出什么樣的結論.
生:我們組的幾個同學畫的直角三角形(如圖2所示)疊合在一起,發現這些直角三角形能互相重合,認為這些直角三角形全等.
師:請學生嘗試畫出下面的圖形:(1)任意畫兩條互相垂直的直線,垂足為D;(2)在其中一條垂線上任取一點A,以這一點為圓心,以大于AD的長為半徑畫弧,這個弧與另一條垂線有兩個交點B,C;(3)連接AB,AC,得到△ABD與△ACD,那么這兩個三角形全等嗎?
生:我們組畫出了如圖3所示的圖形.
師:請同學們用折紙的方法驗證一下△ABD與△ACD是否全等?為什么?
生:△ABD與△ACD全等.因為這兩個三角形折合在一起能互相重合.
師:請同學們畫一畫三角形ABC,使∠B=40°,AB=4 cm,AC=3 cm,然后把所畫圖形放在一起,看它們是否重合?
生:老師,我畫出如圖4所示的圖形,我同桌畫出了如圖5所示的圖形. 這兩個圖形,一個是鈍角三角形,一個是銳角三角形,它們不重合.
師:圖3的△ABD與△ACD具備什么相等的條件?圖4與圖5的兩個三角形具備什么相等的條件?為什么圖3的兩個三角形全等,而圖4與圖5的兩個三角形卻不全等?
生:圖3的△ABD與△ACD具備兩邊一角相等的條件,圖4與圖5的兩個三角形也具備兩邊一角相等的條件. 圖3的兩個三角形全等,是因為這兩個三角形都是直角三角形.
師:從這里可以看出,使用“邊邊角”判定兩個三角形全等,必須是兩個直角三角形. 也就是說,只有當兩個直角三角形,有一條斜邊和一條直角邊分別相等時,這兩個直角三角形才全等. 這就是今天學習的判定兩個直角三角形全等的方法,簡記為“斜邊直角邊”或“HL”,請同學們用圖形語言與符號語言表示這個定理.
生:如圖6所示,在Rt△ABC和Rt△DEF中,因為BC=EF,AC=DF,所以Rt△ABC≌Rt△DEF(HL).
設計意圖 ?在慢慢地操作與教學流程中,引導學生突破重點知識,把學生教活、教深,發展學生的口頭表達、動手操作、演繹推理等能力. 畫圖是歸納結論的有力抓手,也是進一步總結的依據. 本環節學生經歷了三次畫圖,第一次畫圖旨在讓學生通過斜邊直角邊可以確定一個直角三角形,通過學生之間所畫直角三角形的疊合,感受通過斜邊直角邊可以判定兩個直角三角形全等. 第二次畫圖從具體到一般,讓學生再次經歷利用斜邊直角邊可以判定兩個直角三角形全等. 第三次畫圖,雖然也具有兩邊及一角相等,但是它們并不全等,與第二次畫圖對照,突出強調斜邊直角邊定理成立的前提條件是兩個直角三角形. 緩慢的操作為學生提供了充足的思考空間,在學生靜靜地思考與徐徐地交流中,學生體驗了知識的來龍去脈,不僅知其然,也知其所以然,認識由感性上升為理性,實現了思維的突破.
變式應用,拓展延伸
如圖7所示,在△ABC中,AB=AC,DE是過點A的直線,BD⊥DE于點D,CE⊥DE于點E,B,C在DE的同側,且AD=CE. 求證:AB⊥AC.
生:因為BD⊥DE,CE⊥DE,根據垂直的定義,得∠ADB=∠AEC=90°,在Rt△ABD和Rt△ACE中,因為AB=AC,AD=CE,根據斜邊直角邊定理,得Rt△ABD≌Rt△CAE(HL). 根據全等三角形對應角相等,得∠DAB=∠ECA,∠DBA=∠EAC. 根據直角三角形兩銳角互余,得∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,所以∠DAB+∠EAC=90°. 所以∠BAC=180°-(∠BAD+∠CAE)=90°,即AB⊥AC.
師:這位同學能很快抓住題中兩個垂直,及兩組相等的線段,利用斜邊直角邊定理獲證,很好!如果過點A的直線DE與BC相交時,結論還成立嗎?
變式1 ? 在△ABC中,AB=AC,DE是過點A的直線,BD⊥DE于點D,CE⊥DE于點E,B,C在DE的兩側(如圖8所示),且AD=CE,AB與AC仍垂直嗎?若是,請給出證明;若不是,請說明理由.
生:AB⊥AC. 理由如下:因為BD⊥DE,CE⊥DE,根據垂直的定義,得∠ADB=∠AEC=90°,在Rt△ABD和Rt△CAE中,因為AB=AC,AD=CE,根據斜邊直角邊定理,可以得到Rt△ABD≌Rt△CAE(HL). 所以∠DAB=∠ECA,∠DBA=∠EAC. 因為∠CAE+∠ECA=90°,所以∠CAE+∠BAD=90°. 所以∠BAC=90°,即AB⊥AC.
變式2 ?如圖8所示,在△ABC中,∠BAC=90°,AB=AC,AE是過點A的一條直線,且B,C在AE的異側,BD⊥AE于點D,CE⊥AE于點E,求證:BD=CE-DE. 這道試題還能否用斜邊直角邊定理解答呢?為什么?
生:這道題不能用斜邊直角邊定理解答,因為△ABD與△CAE只有一組邊相等.證明如下:因為∠BAC=90°,BD⊥AE,CE⊥AE,所以∠BDA=∠AEC=90°. 因為∠ABD+∠BAE=90°,∠CAE+∠BAE=90°,根據同角的余角相等,得∠ABD=∠CAE,因為AB=AC,在△ABD和△CAE中,因為∠BDA=∠AEC,∠ABD=∠CAE,AB=AC,根據角角邊定理,得△ABD≌△CAE,所以BD=AE,AD=CE,因為AE=AD-DE,所以BD=CE-DE.
設計意圖 ?問題是培養學生思維的有效載體. 問題的呈現,能讓學生在慢交流與慢討論中,凸顯思維過程,實現精確思考,能使學生的思維能力得到培養. 變式訓練,拉長了實踐與應用的過程,緩慢的進程有利于學生體會思維的嚴謹性與數學的縝密性,有些教師認為變式訓練耗時耗力,擾亂了正常的教學預設,但不可否認的是,它有利于學生思維的慢性回歸,能讓學生的思維不斷地向深處漫溯.
慢不是一種重復,而是一種藝術. 只有在慢下腳步后,學生學習才更加充實豐盈[3]. 慢課堂是長效的課堂,是深度教學的課堂.
參考文獻:
[1]楊勇. 初中數學慢教育策略[J]. 中小學班主任,2020(08):52-53.
[2]黃燕紅. 慢教育視閾下的初中數學概念教學研究[D]. 福建師范大學,2018.
[3]孫朝仁,朱桂鳳. 具身認知:數學“慢教育”復習的范式[J]. 教育研究與評論(中學教育教學),2017(10):68-71.

