沉浸式理念下思維導(dǎo)圖在初中數(shù)學(xué)教學(xué)中的應(yīng)用

【摘要】沉浸式教學(xué)之于初中數(shù)學(xué)教學(xué)，就是教師創(chuàng)設(shè)具體的情境，讓學(xué)生沉浸在具體的情境中，從而獲得能力上的發(fā)展。思維導(dǎo)圖之于初中數(shù)學(xué)教學(xué)，就是教師充分拓寬學(xué)生的思路，以各種圖形思維工具將學(xué)生的發(fā)散性思維具體化、可視化[1]。教師將沉浸式理念與思維導(dǎo)圖融合起來應(yīng)用于初中數(shù)學(xué)課堂，能更好地激發(fā)學(xué)生的主觀能動性，并能改進學(xué)生的學(xué)習(xí)方式，促進學(xué)生數(shù)學(xué)學(xué)科素養(yǎng)的提高。

【關(guān)鍵詞】初中數(shù)學(xué);沉浸式;思維導(dǎo)圖

作者簡介：施婧婧（1985—），女，江蘇省南通市啟東市繼述中學(xué)。

沉浸式理念下的初中數(shù)學(xué)教學(xué)需要教師充分調(diào)動學(xué)生的多元感官，以發(fā)揮他們的想象能力、推理能力、判斷能力等。在沉浸式學(xué)習(xí)中，學(xué)生能夠主動積極地參與各項課堂活動，進而獲得真實的情感與學(xué)習(xí)體驗。沉浸式理念下思維導(dǎo)圖的應(yīng)用，是教師針對數(shù)學(xué)學(xué)科的特點而創(chuàng)設(shè)教學(xué)情境，讓學(xué)生置身于思維導(dǎo)圖的學(xué)習(xí)情境中展開一系列的體驗性學(xué)習(xí)。在這樣的教學(xué)情境下，學(xué)生能夠全身心沉浸在思維導(dǎo)圖的建構(gòu)與應(yīng)用中，進而獲得多元化的發(fā)展。

一、預(yù)習(xí)環(huán)節(jié)建構(gòu)思維導(dǎo)圖，活躍學(xué)生的思維

教師在設(shè)計預(yù)習(xí)作業(yè)時，往往是讓學(xué)生做一些題目，促使學(xué)生在做題目的過程中提前理解所要學(xué)習(xí)的內(nèi)容，并且能夠從中發(fā)現(xiàn)一些需要解決的問題。但是，通過這樣的預(yù)習(xí)方式，學(xué)生獲得的認知是碎片化的，他們對整個章節(jié)的知識缺乏系統(tǒng)的認識[2]。因此，教師可以設(shè)計建構(gòu)思維導(dǎo)圖的預(yù)習(xí)作業(yè)，讓學(xué)生將預(yù)習(xí)的內(nèi)容梳理出來，將發(fā)現(xiàn)的問題也呈現(xiàn)出來。教師通過學(xué)生建構(gòu)的思維導(dǎo)圖，能直觀地了解學(xué)生的預(yù)習(xí)情況，也能清晰地判斷新課講授所要聚焦的知識點與能力點。學(xué)生在繪制思維導(dǎo)圖的過程中，往往更容易投入，更容易沉浸在數(shù)學(xué)的世界中，預(yù)習(xí)的效果自然不錯。教師在引導(dǎo)學(xué)生繪制預(yù)習(xí)思維導(dǎo)圖時，一方面，要給學(xué)生充分的自由發(fā)揮空間，思維導(dǎo)圖的形狀、關(guān)鍵詞、主要內(nèi)容等都可以由學(xué)生自由確定;另一方面，教師也可以要求學(xué)生在思維導(dǎo)圖中呈現(xiàn)個性化的內(nèi)容，比如呈現(xiàn)自己發(fā)現(xiàn)的具體問題與存在的困惑等。

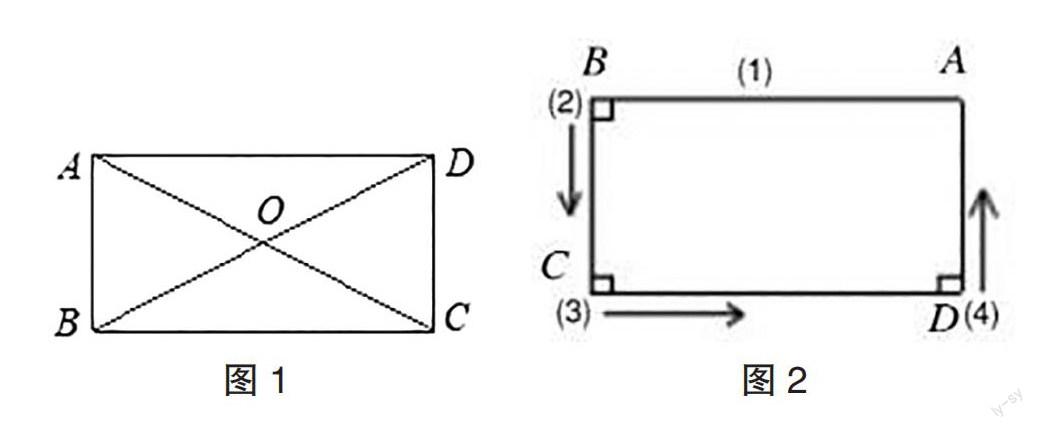
以人教版初中數(shù)學(xué)八年級下冊“矩形的判定”的教學(xué)為例，教師在教學(xué)的過程中給學(xué)生充分的學(xué)習(xí)時間與空間，讓學(xué)生體驗矩形判定方法的探究過程，讓學(xué)生自己體會三種不同的矩形判定方法。教師并沒有直接讓學(xué)生機械地背誦、甚至默寫概念與公式。在學(xué)生掌握矩形的三種判定方法后，教師還引導(dǎo)學(xué)生進行簡單的證明，以進一步培養(yǎng)學(xué)生的邏輯推理能力和演繹能力。在預(yù)習(xí)階段，教師讓學(xué)生以思維導(dǎo)圖的形式將矩形的三種判定方法呈現(xiàn)出來，同時再找對應(yīng)的例子分別展示不同判定方法在具體情境中的應(yīng)用。首先，學(xué)生在畫好的圓圈里寫上中心詞“矩形的判定”。其次，學(xué)生以圓圈為中心向外延伸三個方框，分別寫上：有一個角是直角的平行四邊形是矩形;對角線相等的平行四邊形是矩形;有三個角是直角的四邊形是矩形。最后，學(xué)生以具體的例子展示每種判定方法的具體證明。對于第二種判定方法，有的學(xué)生舉例：如圖1所示，在四邊形ABCD中AB=CD，BC=AD，AC=BD，求證四邊形ABCD是矩形。學(xué)生從AB=CD，BC=AD這兩個條件出發(fā)，得出四邊形ABCD是平行四邊形，進而也得出AB∥CD、∠ABC+∠DCB=180°。接著學(xué)生又從AC=BD，AB=CD，BC=AD這三個條件出發(fā)，得出△ABC≌△DCB、∠ABC=∠DCB=90°，最終證明四邊形ABCD是矩形。對于第三種判定方法，有部分學(xué)生證明不出來，他們就在思維導(dǎo)圖中的舉例部分打上一個問號。這時，教師就第三種判定方法給出更生動的例子：珊珊同學(xué)用畫“邊AB—直角∠B、邊BC—直角∠C、邊CD—直角∠D、邊DA”這樣四個步驟畫出四邊形ABCD，如圖2所示。請問珊珊同學(xué)的判斷對嗎？教師先是指導(dǎo)學(xué)生寫出已知條件：在四邊形ABCD中∠B=∠C=∠D=90°。接著再求證：四邊形ABCD是矩形。學(xué)生從∠B=∠C，得出AB∥CD;再從∠C=∠D，得出BC∥AD，進而得出四邊形ABCD是平行四邊形;最后學(xué)生由∠B=90°這一條件，得出四邊形ABCD是矩形。

在預(yù)習(xí)環(huán)節(jié)應(yīng)用思維導(dǎo)圖，能充分展示學(xué)生的自主學(xué)習(xí)能力。學(xué)生需要自己建構(gòu)獲得的信息;再將抽象的文字轉(zhuǎn)為可視的圖表;最后一目了然地展示自己的問題。預(yù)習(xí)的目的不是讓學(xué)生簡單地做一些題目，背一些書上的公式，而是要讓學(xué)生更多維地參與到新知識的探索中。思維導(dǎo)圖在預(yù)習(xí)環(huán)節(jié)中的應(yīng)用，有利于活躍學(xué)生的思維，為他們后續(xù)更進一步的學(xué)習(xí)打下基礎(chǔ)。

二、課堂教學(xué)環(huán)節(jié)建構(gòu)思維導(dǎo)圖，促進學(xué)生的深度理解

教師在課堂教學(xué)的過程中，希望學(xué)生能完全沉浸在學(xué)習(xí)的情境中，同時希望能充分調(diào)動他們的多元感官，以此達到良好的教學(xué)效果。當(dāng)學(xué)生的大腦動起來、眼睛動起來、雙手動起來的時候，他們的思維必然就集中到課堂教學(xué)的內(nèi)容中。教師在課堂教學(xué)中創(chuàng)設(shè)情境，應(yīng)用思維導(dǎo)圖，能夠幫助學(xué)生清晰地觀察解題的過程，讓學(xué)生深度理解學(xué)習(xí)的內(nèi)容，并讓他們知道自己需要突破的重難點。

以人教版初中數(shù)學(xué)八年級上冊“折疊問題”的教學(xué)為例，教師給學(xué)生設(shè)置這樣的問題情境：在一張矩形的紙片ABCD中，AB=8，如果將紙片進行折疊，使頂點B落在邊AD的E點上，測量得BG=10。當(dāng)折痕的另一端點 F 落在AB邊上時，能不能求出△EFG的面積？當(dāng)折痕的另一端點 F 落在AD邊上時，能不能證明四邊形BGEF為菱形，同時求出折痕GF的長？首先，教師讓學(xué)生將題目中的表述用圖表的形式展示，也就是說，學(xué)生需要根據(jù)文字畫出相應(yīng)的圖形，這對學(xué)生來說有一定的難度。教師引導(dǎo)學(xué)生拿出矩形的紙片按照題目中的步驟，一步步地折疊，在折疊的同時完成圖形的繪制。學(xué)生以中心詞“矩形的變化”建構(gòu)思維導(dǎo)圖，并將圖3、圖4展示。其次，教師讓學(xué)生在繪制的圖形下方以思維導(dǎo)圖的形式呈現(xiàn)解題的過程，但學(xué)生只需要呈現(xiàn)大致的證明方向，不需要呈現(xiàn)詳細的步驟。教師從學(xué)生的思維導(dǎo)圖中，就能判斷他們的思路是否正確，是否需要教師給出一些提示等。對于第一個證明，學(xué)生只在思維導(dǎo)圖下方呈現(xiàn)這樣兩個重要的步驟：一是證明△BFG≌△EFG;二是證明△EAF∽△GHE。最后，由這個簡單的思維導(dǎo)圖，教師清楚地看出學(xué)生思維的過程，放心地讓他們開展具體的證明。

在教學(xué)過程中教師關(guān)注的不能只是學(xué)生最后的解題結(jié)果，而是要關(guān)注學(xué)生解題的過程與思維的活動。在課堂教學(xué)中，教師將思維導(dǎo)圖應(yīng)用于學(xué)生具體的解題過程，能進一步地激活學(xué)生的靈感和數(shù)學(xué)思維，為構(gòu)建高效的課堂教學(xué)提供有效途徑。通過思維導(dǎo)圖的建構(gòu)，一方面，教師知道哪些學(xué)生還需要進一步引導(dǎo)，哪些學(xué)生可以放手讓他們自主地解答。另一方面，學(xué)生能養(yǎng)成良好的解題習(xí)慣，能有條理地運用知識。

三、作業(yè)環(huán)節(jié)建構(gòu)思維導(dǎo)圖，幫助學(xué)生內(nèi)化課堂所學(xué)

教師布置作業(yè)的目的是鞏固學(xué)生認知，發(fā)展學(xué)生能力。在“雙減”的背景下，教師需要減輕學(xué)生的負擔(dān)，需要減少作業(yè)量，但同時需要關(guān)注學(xué)生學(xué)習(xí)的質(zhì)量。教師讓學(xué)生將作業(yè)以思維導(dǎo)圖的方式呈現(xiàn)，能有效地反饋課堂教學(xué)的情況。

以人教版初中數(shù)學(xué)七年級下冊“實際問題與二元一次方程組”的教學(xué)為例，學(xué)生作業(yè)的第一題為：有甲、乙兩個牧童，甲對乙說：“把你的羊給我1只，我的羊就是你的羊的2倍。”乙回答說：“最好還是把你的羊給我1只，我們的羊的數(shù)量就一樣了。”求兩個牧童各有多少只羊？教師讓學(xué)生以思維導(dǎo)圖的形式展示解題的過程。首先，學(xué)生寫下關(guān)鍵詞“經(jīng)典的二元一次方程組應(yīng)用題”。其次，學(xué)生由關(guān)鍵詞引出三個分支：兩個未知數(shù)，分別是甲乙兩牧童各自有的羊的數(shù)量;甲的羊數(shù)+1=（乙的羊數(shù)-1）×2，甲的羊數(shù)-1=乙的羊數(shù)+1;設(shè)甲有x只羊，乙有y只羊。最后，學(xué)生列出方程組 。

學(xué)生如果能建構(gòu)條理清晰的思維導(dǎo)圖，則說明他們能感知這一章節(jié)的基本內(nèi)容，并能掌握具體的解題思路，如此，教師就不需要再讓學(xué)生重復(fù)解決相同的問題。可見，思維導(dǎo)圖在作業(yè)環(huán)節(jié)的應(yīng)用，有利于學(xué)生擺脫繁重的作業(yè)負擔(dān)，有利于學(xué)生課后梳理認知結(jié)構(gòu)與解題思路。

四、反思環(huán)節(jié)建構(gòu)思維導(dǎo)圖，實現(xiàn)學(xué)生反思的可視化

教師的教學(xué)如果沒有反思，就不是精準(zhǔn)的教學(xué)。同樣，學(xué)生的學(xué)習(xí)如果沒有反思，就不是有效的學(xué)習(xí)。教師的反思能更好地對接學(xué)生的學(xué)，學(xué)生的反思能更好地對接教師的教。學(xué)生通過反思還能發(fā)現(xiàn)自己的不足，進而更好地提升自己。如果學(xué)生在反思環(huán)節(jié)能應(yīng)用思維導(dǎo)圖，就能一目了然地看到自己的亮點與自己存在的不足。也就是說，思維導(dǎo)圖實現(xiàn)了學(xué)生反思的可視化。只要學(xué)生打開反思記錄本，自己所畫的思維導(dǎo)圖就能清楚地呈現(xiàn)在眼前，借助思維導(dǎo)圖，學(xué)生就能很快地想起相關(guān)的學(xué)習(xí)體驗，從而促進新知識的學(xué)習(xí)和新問題的解決。

以人教版初中數(shù)學(xué)九年級上冊“直線和圓的位置關(guān)系”的教學(xué)為例，教師呈現(xiàn)這樣的題目：△ABC中，∠C=90°，BC=4，AC=3，求△ABC的內(nèi)切圓⊙O的半徑r，如圖5所示。

學(xué)生第一次做題時是這樣做的：第一，連接OD、OF，因為⊙O切△ABC的邊BC、AC于點D、F，所以推斷出OD⊥BC，OF⊥AC;同時又因為∠C=90°，所以四邊形ODCF是矩形;第二，由四邊形ODCF是矩形這一條件得出OD=OF，所以矩形ODCF是正方形;第三，CD=CF=OD=r，BD=4-r，AF=3-r;第四，因為AB切⊙O于E，所以BE=BD，AE=AF，BD+AF=AB;最終求出r=1。

當(dāng)學(xué)生正確解答這道題后，教師給予學(xué)生充分的肯定，并引導(dǎo)學(xué)生進行反思，這道題有沒有其他解決的方法。學(xué)生思考后發(fā)現(xiàn)，這道題也可以采用面積變換的方法求解。首先，學(xué)生連接OA、OB、OC、OD、OE、OF，由⊙O是△ABC的內(nèi)切圓，得出OD⊥BC，OE⊥AB，OF⊥AC。其次，由∠C=90°，BC=4，AC=3，得出AB=5。最后，學(xué)生列出等量關(guān)系，S△AOB+S△BOC+

S△AOC=S△ABC=AB·r+BC·r+AC=AC·BC，即（3+4+5）r=3×4，r=1。基于反思，學(xué)生建構(gòu)這樣的思維導(dǎo)圖，中心詞“求△ABC的內(nèi)切圓⊙O的半徑r的兩種方式”，中心詞下面的兩個分支中，學(xué)生直接呈現(xiàn)的是兩種具體的做輔助線的方式。下一次，學(xué)生再遇到此類題目時，自然就想到這樣的兩種直觀的圖。可見，借助思維導(dǎo)圖能讓反思變得直觀，更容易幫助學(xué)生舉一反三。對于數(shù)學(xué)學(xué)習(xí)來說，反思很重要，而要讓學(xué)生能沉浸式地反思，教師的科學(xué)引導(dǎo)就很重要。教師將思維導(dǎo)圖融入反思，改進了學(xué)生反思的方式，幫助學(xué)生更好地理清思路，從而提高學(xué)生的思維能力。

結(jié)語

教師根據(jù)學(xué)生的不同認知狀況，創(chuàng)設(shè)更為適切的情境，讓學(xué)生從繪制思維導(dǎo)圖中獲得不一樣的學(xué)習(xí)體驗。而學(xué)生在沉浸式的教學(xué)情境下應(yīng)用思維導(dǎo)圖學(xué)習(xí)數(shù)學(xué)知識，能提高學(xué)習(xí)的積極性，更全神貫注地學(xué)習(xí)，從而讓自身的數(shù)學(xué)能力在潛移默化中得到提高。在以后的教學(xué)中，教師要不斷創(chuàng)新沉浸式應(yīng)用思維導(dǎo)圖的教學(xué)方式，激發(fā)數(shù)學(xué)課堂的魅力，以更好地挖掘?qū)W生的潛能，凸顯思維導(dǎo)圖的教學(xué)價值。

【參考文獻】

[1]章禮滿.沉浸于學(xué)，樂在其中：芻議沉浸式教學(xué)對初中數(shù)學(xué)教學(xué)的啟發(fā)與思考[J].數(shù)學(xué)教學(xué)通訊，2021（35）：19-20.

[2]趙洋，黃秦安.思維導(dǎo)圖在初中數(shù)學(xué)課堂教學(xué)中的功能與價值[J].數(shù)學(xué)通報，2020，59（05）：21-24，45.