初中數(shù)學(xué)培養(yǎng)學(xué)生問題意識的教學(xué)實踐

常娟

【摘 要】 數(shù)學(xué)是一門邏輯性較強的學(xué)科，因此在實踐教學(xué)過程中需要學(xué)生保持良好的鉆研精神，主動深入到知識的更深層領(lǐng)域進行探索，如此才能夠更加靈活地掌握數(shù)學(xué)知識，并把握數(shù)學(xué)思想的優(yōu)秀內(nèi)涵，基于此，本文對初中數(shù)學(xué)教學(xué)中學(xué)生問題意識的培養(yǎng)策略展開了研究，從培養(yǎng)學(xué)生問題意識的重要性入手，進而討論在數(shù)學(xué)實踐教學(xué)過程中需要把握的要點以及培養(yǎng)學(xué)生問題意識的有效策略，希望能夠以此促進初中數(shù)學(xué)教學(xué)質(zhì)量的整體提升，

【關(guān)鍵詞】 初中數(shù)學(xué);實踐教學(xué);問題意識

所謂“問題意識”，強調(diào)的是學(xué)生在學(xué)習(xí)過程中自主發(fā)現(xiàn)問題并解決問題的能力.其在數(shù)學(xué)教學(xué)過程中的主要價值，體現(xiàn)在能夠有效調(diào)動學(xué)生利用已有的知識經(jīng)驗，去對陌生的知識展開獨立探索與理解，這種行為能夠有效地將學(xué)生的思維方式、知識儲備、認知能力等內(nèi)容聯(lián)系在一起，從而切實提高學(xué)生的數(shù)學(xué)能力.因此初中數(shù)學(xué)教師在實踐教學(xué)過程中，應(yīng)當注重采用靈活的教學(xué)手段，在課堂中激發(fā)學(xué)生的審辨思維，以此實現(xiàn)培養(yǎng)學(xué)生問題意識的目的.

1 培養(yǎng)學(xué)生問題意識的意義

1.1 有利于開發(fā)學(xué)生的學(xué)習(xí)思維

問題意識的培養(yǎng)，可以使學(xué)生在進行學(xué)習(xí)的過程中，對數(shù)學(xué)知識產(chǎn)生更深層次的思考，而不再僅僅只是跟隨教師的思路進行僵化地學(xué)習(xí).此外，問題的產(chǎn)生源于學(xué)生的認知沖突，而學(xué)生在解決問題的過程中，實質(zhì)上是完成了一次知識“打破——重建”的過程，可以促使學(xué)生的認知能力得到整體的提升.并且結(jié)合教師傳遞的內(nèi)容，使學(xué)生對于數(shù)學(xué)知識產(chǎn)生更加具有個人色彩的分析，從而在一定程度上促使數(shù)學(xué)知識真正內(nèi)化為學(xué)生的個人儲備[1].

1.2 有利于激發(fā)學(xué)生的學(xué)習(xí)熱情

問題意識的培養(yǎng)實質(zhì)上強調(diào)的是師生在課堂中的交流互動.作為教學(xué)活動中的共同參與者，當學(xué)生對知識產(chǎn)生疑惑時最好的交流對象便是教師，而教師可以根據(jù)學(xué)生提出的問題，敏銳地捕捉到學(xué)生的學(xué)習(xí)層次，以及其此刻的關(guān)注點在哪里，從而可以適當?shù)匾龑?dǎo)學(xué)生向某個方向進行探索，幫助其去尋找解決問題的途徑，并在此過程中使學(xué)生完成了知識構(gòu)建任務(wù).這樣的教學(xué)方式相比于傳統(tǒng)的教學(xué)模式來說，無疑要更加具有吸引力，同時也有效地兼顧到學(xué)生的個體差異問題，因此可以提供給學(xué)生更好的學(xué)習(xí)體驗.

1.3 有利于培養(yǎng)學(xué)生的自主學(xué)習(xí)能力

當學(xué)生發(fā)現(xiàn)問題之后，引導(dǎo)學(xué)生去解決問題的過程，無疑也是一種有效增強學(xué)生學(xué)習(xí)能力的方式.并且由于問題的提出源自于學(xué)生內(nèi)心的個人疑惑，因此學(xué)生在解決問題的過程中往往會爆發(fā)出更加強大的學(xué)習(xí)動力，從而不但能夠促使問題得到有效解決，還能夠幫助學(xué)生掌握正確的學(xué)習(xí)方法，并在此過程中強化了學(xué)生的自主學(xué)習(xí)能力以及學(xué)習(xí)信心[2].

2 培養(yǎng)學(xué)生問題意識的要點

2.1 課標為準

在新時期素質(zhì)教育的背景下，培養(yǎng)學(xué)生的核心素養(yǎng)是教學(xué)活動開展的主要基調(diào)，因此初中數(shù)學(xué)教師應(yīng)當深刻領(lǐng)悟當前的抽象概括、演繹證明、符號表達、數(shù)據(jù)處理、空間想象、運算求解等數(shù)學(xué)核心素養(yǎng)內(nèi)容，并在培養(yǎng)學(xué)生問題意識的過程中使學(xué)生能夠透過這六大層面去思考問題，進而為學(xué)生提供綜合發(fā)展的個性化學(xué)習(xí)平臺，使學(xué)生的學(xué)習(xí)能力能夠在此過程中得到有效提升.

2.2 課程為基

數(shù)學(xué)作為一項基礎(chǔ)學(xué)科，其自身最大的教學(xué)價值體現(xiàn)在實用性方面.因此教師在為學(xué)生開展教學(xué)活動的過程中，需要以教材為基礎(chǔ)，引導(dǎo)學(xué)生去思考并發(fā)掘教材與現(xiàn)實生活中的銜接點，從而提高學(xué)生對教材內(nèi)容的理解，并加強學(xué)生對數(shù)學(xué)知識的應(yīng)用能力.例如在學(xué)習(xí)“有理數(shù)加法”的過程中，教師不僅僅需要強化學(xué)生的符號表達能力，同時更要引導(dǎo)學(xué)生思考有理數(shù)運算在現(xiàn)實生活中具體有哪些使用途徑，如此才能夠擴寬學(xué)生思考問題的深度與寬度，將問題意識的培養(yǎng)落實在數(shù)學(xué)課堂的每個細節(jié)當中.

2.3 學(xué)生為主

在培養(yǎng)學(xué)生問題意識的過程中，教師需要注重在課堂中體現(xiàn)出“以生為本的教學(xué)理念，并為學(xué)生構(gòu)建和諧平等的課堂氛圍，如此才能夠卸下學(xué)生的心理壓力，使學(xué)生主動大膽地在課堂中提出與教師不一樣的見解.除此之外，面對學(xué)生提出的問題，教師應(yīng)當適時給予一定的鼓勵和肯定，使學(xué)生能夠做到善于提問、樂于提問，從而體現(xiàn)出新時期數(shù)學(xué)課堂的開放性[3].

3 培養(yǎng)學(xué)生問題意識的有效策略

3.1 引發(fā)學(xué)生認知沖突，激起學(xué)生提問欲望

在實踐教學(xué)過程中，教師需要根據(jù)學(xué)生的實際情況來設(shè)置教學(xué)內(nèi)容，并借此來為學(xué)生制造認知障礙，使學(xué)生的思維在既有知識經(jīng)驗與課堂新知之間產(chǎn)生碰撞，并利用這樣的思維碰撞，來調(diào)動學(xué)生的學(xué)習(xí)積極性，使其能夠主動對知識展開探索，并且在此過程中，教師需要對學(xué)生的學(xué)習(xí)狀態(tài)保持密切關(guān)注，特別是學(xué)生在表現(xiàn)出遇到學(xué)習(xí)困難的時候，教師需要引導(dǎo)學(xué)生準確地將自身遇到的困難描述出來，從而形成學(xué)生在學(xué)習(xí)過程中所產(chǎn)生的具體疑問[4].

例如 在學(xué)習(xí)一元二次方程的過程中，教師可以為學(xué)生設(shè)置這樣的教學(xué)步驟：

已知一個一元二次方程式：2（x-3）=（x-3）2，按照學(xué)生已有的知識經(jīng)驗去進行解答，可以通過兩邊同時除以z一3的方式得到2=x-3，從而得出z一5;而在教學(xué)過程中，教師在黑板上給出另一種解法，也就是利用因式分解的方式來求解一元二次方程，通過移項，可以得到新的等式：2（x-3）一（x一3）2=0，按照因式分解的解法，可以得到（x-3）（2-x+3）=0，解得x1=5，x2=3.

通過觀察解題步驟，學(xué)生很容易產(chǎn)生認知障礙，并向教師提問：為什么兩種算法的計算結(jié)果不同呢？而教師則可適時引導(dǎo)學(xué)生去思考“解方程時一般不能兩邊同除以含有未知數(shù)的代數(shù)式這一知識點，并逐漸引導(dǎo)學(xué)生去思考不能這樣做的原因，從而使學(xué)生能夠不斷在學(xué)習(xí)過程中發(fā)掘新的問題.

3.2 尋找合適問題載體，培養(yǎng)學(xué)生提問技巧

培養(yǎng)學(xué)生的問題意識，首先需要保證學(xué)生“會問”.因此在實踐教學(xué)過程中，教師可以適當調(diào)整教材中的習(xí)題、知識點，來為學(xué)生設(shè)置合適的問題載體，以此來培養(yǎng)學(xué)生的提問技巧，使其掌握思考問題的正確切人點[5].

3.2.1 一題多變，培養(yǎng)學(xué)生問題技巧，教師在為學(xué)生開展解題教學(xué)的過程中，可以適當針對數(shù)學(xué)習(xí)題進行相應(yīng)的改編，以此來培養(yǎng)學(xué)生的發(fā)散思維，使學(xué)生掌握正確的提問方式.

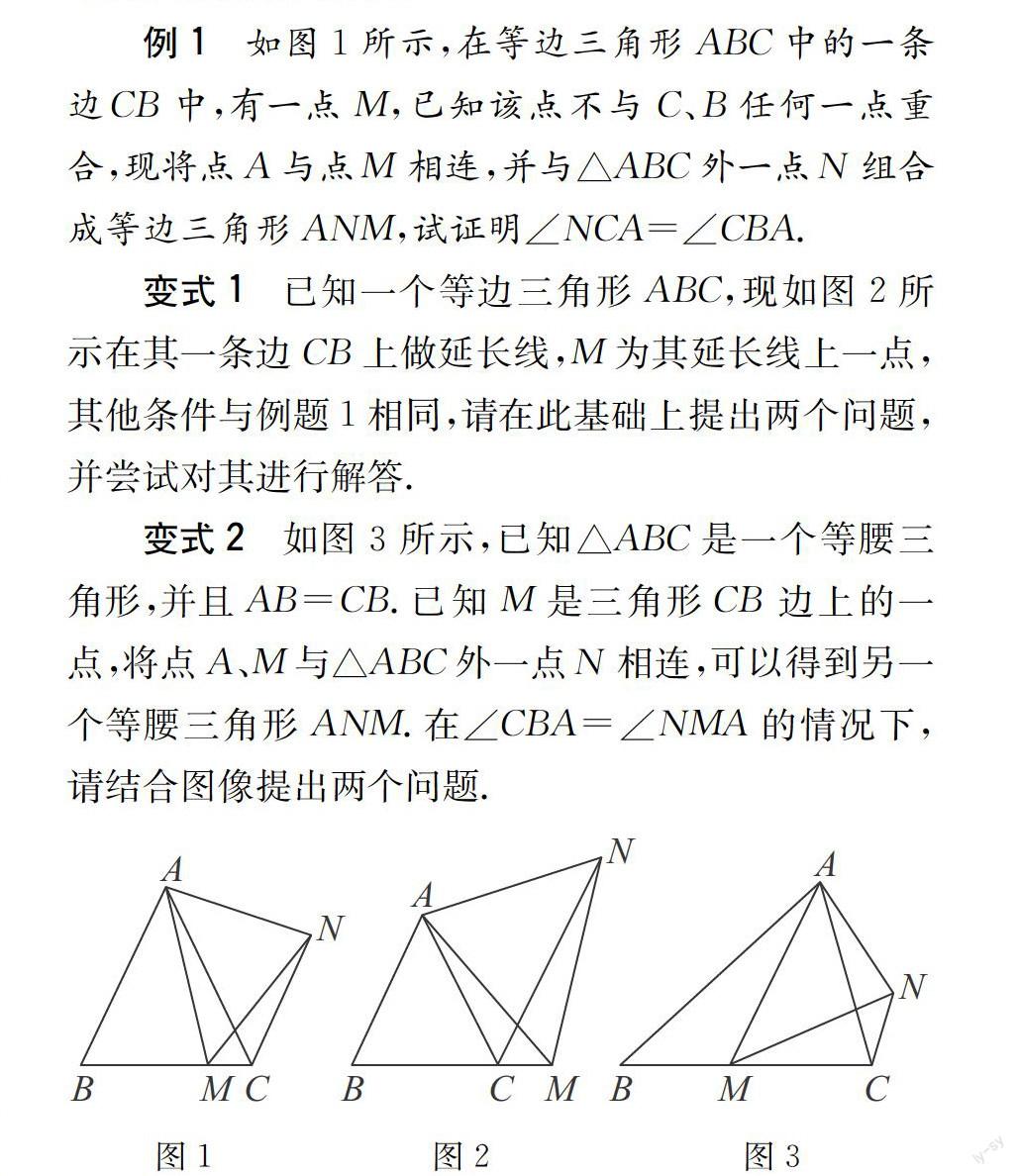
例1 如圖1所示，在等邊三角形ABC中的一條邊CB中，有一點M，已知該點不與C、B任何一點重合，現(xiàn)將點A與點M相連，并與△ABC外一點N組合成等邊三角形ANM，試證明∠NCA=∠CBA.

變式1 已知一個等邊三角形ABC，現(xiàn)如圖2所示在其一條邊CB上做延長線，M為其延長線上一點，其他條件與例題1相同，請在此基礎(chǔ)上提出兩個問題，并嘗試對其進行解答.

變式2 如圖3所示，已知△ABC是一個等腰三角形，并且AB= CB.已知M是三角形CB邊上的一點，將點A、M與△ABC外一點N相連，可以得到另一個等腰三角形ANM.在∠CBA=∠N2A的情況下，請結(jié)合圖像提出兩個問題.

通過這樣的立體改變，可以使數(shù)學(xué)課堂中的解題教學(xué)更加具有開放性，同時有利于學(xué)生對數(shù)學(xué)問題產(chǎn)生更加深刻地思考.并且能夠幫助學(xué)生通過知識遷移的方式，對提出的問題進行解答，這樣的方式不僅能夠充分開發(fā)學(xué)生的思維潛能，同時也有利于學(xué)生解決問題的能力提升.

3.2.2 尋找知識內(nèi)在聯(lián)系，培養(yǎng)學(xué)生提問技巧.除了習(xí)題教學(xué)之外，知識點教學(xué)也是培養(yǎng)學(xué)生問題意識的有效方式之一.在為學(xué)生講解新課的過程中，教師可以通過問題鏈的形式來為學(xué)生設(shè)計教學(xué)內(nèi)容，使學(xué)生能夠根據(jù)教師的問題引導(dǎo)，逐層深入地去對某一知識點展開探索，如此不僅能夠幫助學(xué)生掌握正確的提問技巧，同時還能夠為學(xué)生構(gòu)建條理清晰的知識框架，使學(xué)生對教材內(nèi)容的理解更加全面.

例如 學(xué)生學(xué)習(xí)了二次函數(shù)后，教師可以為學(xué)生設(shè)計這樣一條問題鏈：已知有一個二次函數(shù)y=x2 -6x-7，那么請問：

（1）能否描述該函數(shù)在坐標軸中的圖像具有怎樣的特點？

（2）能否通過圖像來判斷該函數(shù)的解？

（3）怎樣確定函數(shù)的增減性？

（4）判斷函數(shù)與坐標軸之間的交點坐標.

（5）怎樣移動函數(shù)y=x2，可以得到函數(shù)y =x2 - 6x-7 ？

學(xué)生在思考以上問題的過程中，不僅能夠總結(jié)出二次函數(shù)的一些特點，同時還能夠根據(jù)教師的問題設(shè)置逐步深入了解教材中的知識內(nèi)容.并且這樣的提問方式還能夠?qū)W(xué)生形成一定啟發(fā)作用，使學(xué)生學(xué)會通過逆向思維的方式進行提問，如此在提出問題的同時，也使學(xué)生掌握了清晰的學(xué)習(xí)線索.

3.3 巧借分組學(xué)習(xí)優(yōu)勢，引導(dǎo)學(xué)生發(fā)現(xiàn)問題

在實踐教學(xué)過程中，學(xué)生個人的思維能力是有限的，因此教師可以鼓勵學(xué)生以小組結(jié)合的方式進行學(xué)習(xí)談?wù)摚⒋偈箤W(xué)生在互相討論的過程中交換彼此對知識的看法，從而使學(xué)生能夠根據(jù)彼此對于知識不同的見解而產(chǎn)生新的疑問，如此不僅能夠直接產(chǎn)生問題，展開進一步的知識探索，還能夠引導(dǎo)學(xué)生通過合作的形式去解決問題，在有效培養(yǎng)學(xué)生問題意識的同時，也幫助學(xué)生掌握了解決問題的有效方式，使課堂的教學(xué)效率得到提高[6].

例如 在學(xué)習(xí)“圖形與旋轉(zhuǎn)”的過程中，教師可以讓學(xué)生以小組討論的形式總結(jié)圖形在旋轉(zhuǎn)過程中的一些特點.而在討論過程中，學(xué)生會發(fā)現(xiàn)旋轉(zhuǎn)與對稱之間似乎存在著某些相似之處，那么是否可以說二者視為一體？于是學(xué)生可以帶著這樣的問題，詳細討論“對稱中心與旋轉(zhuǎn)中心、對稱與旋轉(zhuǎn)”的特點，并在總結(jié)二者的共同點基礎(chǔ)之上，討論旋轉(zhuǎn)與對稱之間存在著哪些區(qū)別.

3.4 巧妙構(gòu)設(shè)問題情境，引導(dǎo)學(xué)生發(fā)現(xiàn)問題

引導(dǎo)學(xué)生獨立發(fā)現(xiàn)問題，使其對數(shù)學(xué)知識產(chǎn)生疑惑，才能夠有效培養(yǎng)學(xué)生的問題意識，進而使其養(yǎng)成獨立探究的良好學(xué)習(xí)習(xí)慣，為此教師需要采取一定的教學(xué)措施，通過引發(fā)學(xué)生的好奇心理，幫助其敏銳察覺到學(xué)習(xí)過程中的問題所在.為此，在實踐教學(xué)過程中，教師可以把握教材中的關(guān)鍵要素，以此為基礎(chǔ)為學(xué)生架構(gòu)問題情境，促使學(xué)生能夠基于既有知識經(jīng)驗對事物進行思考，從而引發(fā)認知沖突，并由此產(chǎn)生對知識的探究欲望.這一點不僅是培養(yǎng)學(xué)生問題意識的關(guān)鍵，同樣也是促使其進行有效自主學(xué)習(xí)的契機.

例如 在學(xué)習(xí)圖形的“展開與折疊一課中，教師可以利用多媒體課件作為構(gòu)建問題情境的平臺，向?qū)W生展示正方體結(jié)構(gòu)的幾種不同展開平而圖，并要求學(xué)生在腦海中想象這些圖形需要經(jīng)過怎樣的折疊才能夠還原成一個正方體結(jié)構(gòu)，而在教師展示的圖形中，存在個別圖形是無法組合成正方形的，學(xué)生經(jīng)過想象陷入思維誤區(qū)后，便會不由自主產(chǎn)生疑惑，同時主動通過實踐操作的方式來還原這幾個圖形是否能夠折疊為正方形.通過這一過程，學(xué)生不儀產(chǎn)生了學(xué)習(xí)問題，同時還能夠主動將學(xué)習(xí)想法付諸于實踐，從而有效提高了自身的學(xué)習(xí)效率.因此在實踐教學(xué)過程中，教師應(yīng)當善于使用不同的手段與技巧來對學(xué)生進行指引，使學(xué)生的問題意識得到有效引導(dǎo).

4 結(jié)語

綜上所述，在實踐教學(xué)過程中，培養(yǎng)學(xué)生的問題意識不但能夠提高學(xué)生的學(xué)習(xí)能力，同時還能夠加強學(xué)生的探索精神，使其在進行數(shù)學(xué)學(xué)習(xí)的過程中，能夠主動發(fā)散自身思維，對數(shù)學(xué)知識進行深層思考，從而有效地提高了初中數(shù)學(xué)課堂的教學(xué)質(zhì)量，

參考文獻：

[1]陳國棟，淺談初中數(shù)學(xué)教學(xué)中如何培養(yǎng)學(xué)生的問題意識[J].中學(xué)課程輔導(dǎo)（教學(xué)研究），20 1 9，13（26）：68.

[2]王秋蓉，小組合作學(xué)習(xí)模式在初中數(shù)學(xué)教學(xué)中的應(yīng)用分析[J].中學(xué)課程輔導(dǎo)（教學(xué)研究），201 9，13（12）：102.

[3]歐毅.初中數(shù)學(xué)教學(xué)中培養(yǎng)學(xué)生問題意識的策略探究[J].少男少女，20 1 8.2（15）：16-18.

[4]鞏玉英，田承恩，初中數(shù)學(xué)應(yīng)用問題中滲透數(shù)學(xué)建模思想的策略研究[J].中學(xué)課程輔導(dǎo)（教學(xué)研究），2020，14（33）：155-156.

[5]江照亮.初中數(shù)學(xué)教學(xué)中學(xué)生歸納意識的培養(yǎng)策略分析[J].中學(xué)課程輔導(dǎo)（教學(xué)研究），201 8，12（19）：40.

[6]吳海燕.初中數(shù)學(xué)“問題串”教學(xué)的策略分析[J].中學(xué)課程輔導(dǎo)（教學(xué)研究），2020，14（15）：59.