應(yīng)用轉(zhuǎn)化策略，沖破思維阻隔

黎敏燕

【摘要】轉(zhuǎn)化思想作為解決問題的策略之一，在小學(xué)數(shù)學(xué)教學(xué)中有著非常廣泛的應(yīng)用。巧妙地運(yùn)用轉(zhuǎn)化思想，有利于沖破思維阻隔，實(shí)現(xiàn)遷移學(xué)習(xí)，實(shí)現(xiàn)“以學(xué)生為中心”的課堂教學(xué)，有效地提高學(xué)生的思維能力，打造“品質(zhì)課堂”。

【關(guān)鍵詞】小學(xué)數(shù)學(xué);品質(zhì)課堂;轉(zhuǎn)化思想;操作過程

轉(zhuǎn)化思想作為解決數(shù)學(xué)問題策略之一，在小學(xué)數(shù)學(xué)教學(xué)中應(yīng)用非常廣泛。無(wú)論是計(jì)算三角形、梯形面積時(shí)，還是計(jì)算圓柱體、圓錐體、不規(guī)則物體體積時(shí)，都要用到轉(zhuǎn)化的方法。在學(xué)習(xí)中，如果學(xué)生學(xué)會(huì)把生活問題數(shù)學(xué)問題化，把繁雜問題簡(jiǎn)單化，把抽象問題直觀化。有利于沖破思維阻隔，實(shí)現(xiàn)學(xué)習(xí)遷移，促進(jìn)“雙主-對(duì)話-合作”教學(xué)模式的構(gòu)建，提高品質(zhì)課堂的質(zhì)量。

那如何應(yīng)用轉(zhuǎn)化思想這一策略，幫助學(xué)生沖破思維阻隔，提高品質(zhì)課堂效率？

筆者認(rèn)為在數(shù)學(xué)教學(xué)活動(dòng)中適時(shí)滲透轉(zhuǎn)化思想，是實(shí)施轉(zhuǎn)化策略最有效的途徑和方法。

一、巧用轉(zhuǎn)化思想，化“生疏”為“熟悉”

“使用教材，用活教材”是教師上好課、提高課堂質(zhì)量的基本要求。以人教版《義務(wù)教育教科書 數(shù)學(xué)》六年級(jí)上冊(cè)的‘按比分配’的課堂教學(xué)為例，發(fā)表筆者的見解。

（一）用活教材教，化“生疏”為“熟悉”

品質(zhì)課堂是“以學(xué)生為主體”的高效的課堂教學(xué)。為實(shí)現(xiàn)以生為本，讓學(xué)生更好的認(rèn)識(shí)“按比分配”的本質(zhì)，教者打破了一般數(shù)學(xué)課堂的慣例，將“按比分配”的課例與美術(shù)學(xué)科進(jìn)行有機(jī)整合，在課前精心設(shè)計(jì)“學(xué)生動(dòng)手操作”的前置活動(dòng)，引導(dǎo)學(xué)生動(dòng)手操作：

操作活動(dòng)：共用5杯藍(lán)墨水和紅墨水（每杯50ml），按一定的比例進(jìn)行調(diào)色試驗(yàn)，得到250ML深淺不一的紫墨水。

在此基礎(chǔ)上，教者將相關(guān)數(shù)據(jù)和敘事的內(nèi)容改編成“按比分配”例題進(jìn)行教學(xué)。即把原例題改為：

教者在不改變“按比分配”解決問題主旨的情況下，活用教材教，將濃縮液、稀釋液等陌生概念，轉(zhuǎn)變成學(xué)生熟悉的藍(lán)墨水、紅墨水、紫墨水，使例題更接近于學(xué)生的生活經(jīng)驗(yàn)，化“生疏”為“熟悉”，便于學(xué)生理解，為學(xué)習(xí)新知做好充分的鋪墊。

（二）轉(zhuǎn)化范圍和方向，用“舊”解“新”

“按比分配”由“平均分”延伸而來(lái)。為此，教學(xué)中要尊重編者意圖，利用“比的意義”，引導(dǎo)學(xué)生運(yùn)用已有知識(shí)和遷移規(guī)律，把新問題轉(zhuǎn)化為 “平均分問題”或“分?jǐn)?shù)乘法問題”進(jìn)行解題。

1.重視理解，為實(shí)現(xiàn)范圍和方向轉(zhuǎn)化奠基

在教學(xué)活動(dòng)中，實(shí)現(xiàn)師生、生生對(duì)話，啟發(fā)學(xué)生理解題意，轉(zhuǎn)變解決問題的思路、方向，找到多種解題方法。

教學(xué)片段一

師：請(qǐng)仔細(xì)閱讀題目，從中你知道哪些數(shù)學(xué)信息和問題？（學(xué)生自主閱讀多人回答后板書）

師：1∶4是誰(shuí)和誰(shuí)的比？【板書：比】

預(yù)設(shè)：1∶4是藍(lán)墨水和紅墨水的比

師：你是如何理解1：4的？

預(yù)設(shè)：藍(lán)墨水有1份，紅墨水有4份。 藍(lán)墨水占這瓶墨水的，紅墨水占這瓶墨水的。

師：是的，藍(lán)墨水份數(shù)+紅墨水份數(shù)=紫墨水份數(shù)，共5份。【板書：和】

師：250ml是誰(shuí)的體積？

預(yù)設(shè)：藍(lán)墨水體積+紅墨水體積=紫墨水體積。

就這樣學(xué)生能從題目中很快地找到有效的數(shù)學(xué)信息，理清要求的問題。抓住關(guān)鍵句（藍(lán)墨水和紅墨水按1∶4的，調(diào)配250mL紫墨水）理解題意，初步感知藍(lán)墨水、紅墨水和紫墨水之間的關(guān)系，初步將比轉(zhuǎn)化成分?jǐn)?shù)，為順利解題掃除阻隔。

2.注重分析，易于學(xué)會(huì)

利用數(shù)形結(jié)合思想，借助線段圖，能揭示條件與條件、條件與問題之間的關(guān)系，把數(shù)轉(zhuǎn)化為形，從而激活學(xué)生的解題思路。

教學(xué)片段二

師：剛才我們抓住關(guān)鍵句，初步理解題意。接著是解決問題的第二步——分析與解答。你能用畫圖的方式表示題意嗎？請(qǐng)你們小組合作學(xué)習(xí)，按要求完成活1。

活動(dòng)1：

1.畫一畫：嘗試獨(dú)立畫圖表示題意

2.說一說：小組內(nèi)說一說，你是怎樣用圖來(lái)表示題意的？

（1）我畫了（? ? ? ? ? ）表示（? ?）墨水的數(shù)量，（? ? ）墨水有1份，（? ? ? ）墨水有（? ? ?）份，一共（? ? ?）份。

（2）我畫了（? ? ? ? ）表示（? ?）墨水的數(shù)量，把（? ? ? ）看作單位“1”，平均分成（? ? ?）份，藍(lán)墨水占這瓶墨水的（? ? ），紅墨水占這瓶墨水的（? ? ）。

師：誰(shuí)來(lái)展示？（學(xué)生展示畫圖并說一說如何用圖表示題意）

預(yù)設(shè)1：我畫了一個(gè)長(zhǎng)方形表示紫墨水，共5份，其中藍(lán)墨水有1份，紅墨水有4份。

預(yù)設(shè)2：我畫了這一條線段表示紫墨水，把這瓶紫墨水看作單位“1”平均分成5份，藍(lán)墨水的體積占這瓶墨水的，紅墨水的體積占這瓶墨水的。

預(yù)設(shè)3：我畫了一條線段表示紫墨水，把它看作單位“1”平均分成5份，藍(lán)墨水的體積占這瓶墨水的1份 ，紅墨水的體積占這瓶墨水的 4份。

師生小結(jié)：在分析題意時(shí)，我們用畫一畫、說一說的方法借助直觀圖或線段圖理解了題意。

師：根據(jù)我們剛才的分析，你能嘗試獨(dú)立列式計(jì)算嗎？現(xiàn)在請(qǐng)你試著完成活動(dòng)。

活動(dòng)2：

1.算一算：借助圖形，獨(dú)立列式解答藍(lán)墨水和紅墨水各是多少？

2.說一說：小組成員之間互相說一說，每一步求什么？

3.想一想：你還有其他方法嗎？

師：誰(shuí)來(lái)展示你的算法？（學(xué)生展示）

方法一（歸一法）：

紫墨水平均分成的份數(shù)：1+4=（份）

每份數(shù)：250÷5=50（mL）

藍(lán)墨水的體積：50×1=50（mL）

紅墨水的體積：50×4=200（mL）

生：我是這樣算的， 1+4得到總份數(shù)，250÷5得每份數(shù)，再用每份數(shù)分別乘藍(lán)墨水和紅墨水的所占的份數(shù)，就能求出各自的體積。

明確：先求總份數(shù)，再求每份數(shù)，最后求各部分?jǐn)?shù)，是用歸一法解。

方法二（轉(zhuǎn)化法）：

紫墨水平均分成的份數(shù)：1+4=5（份）

紅墨水的體積：250×=50（mL）

藍(lán)墨水的體積：250×=200（mL）

生：我把1：4轉(zhuǎn)化為份數(shù)，先分別算出紅墨水、藍(lán)墨水占總體積的幾分之幾，最后求一個(gè)數(shù)的幾分之幾是多少？

強(qiáng)調(diào)：將比分別看作1份和4份先求各部分的數(shù)占總數(shù)的幾分之幾，最后用分?jǐn)?shù)乘法解決問題。這是用轉(zhuǎn)化的方法解題。

以上教學(xué)敢于放手讓學(xué)生運(yùn)用數(shù)與形結(jié)合的思想，揭示條件與問題的關(guān)系，尋找到多種解題方法。方法1的思路是“平均分”（如按1∶4分，也就是把總量平均分成（1+4）份。），方法2的思路是轉(zhuǎn)化成分?jǐn)?shù)乘法（利用比和分?jǐn)?shù)的關(guān)系，把問題轉(zhuǎn)化為求一個(gè)數(shù)的幾分之幾是多少。）以上教學(xué)片段，是轉(zhuǎn)化策略的具體運(yùn)用，將“新知”傳為“舊知”，從而化“難”為“易”。

二、巧用轉(zhuǎn)化思想，化“繁”為“簡(jiǎn)”

繁雜的數(shù)據(jù)，雜而難的數(shù)量關(guān)系往往成為學(xué)生解題的障礙。為了更好地解這個(gè)問題，可引導(dǎo)學(xué)生轉(zhuǎn)換思維路徑，變復(fù)雜為簡(jiǎn)單，使問題迎刃而解。

下面將從兩個(gè)例子分享筆者的講解。

例1：某校出操時(shí)站著左右兩個(gè)方陣，左方陣人數(shù)與右方陣人數(shù)的比是3：4，如果右方陣的60人到左方陣，這時(shí)左方陣的人數(shù)是右方陣人數(shù)的，某校共有學(xué)生多少人？

此題中分率對(duì)應(yīng)著不同的單位“1”，這使得例題的數(shù)量關(guān)系繁瑣而復(fù)雜，學(xué)生面對(duì)該題會(huì)束手無(wú)策。由于這所學(xué)校總?cè)藬?shù)始終不變，此時(shí)可引導(dǎo)學(xué)生合作學(xué)習(xí)，通過思考并畫圖輔助解題。學(xué)生會(huì)得到以下思路：

通過這樣轉(zhuǎn)化，都把出操的總?cè)藬?shù)看作單位“1”，求出左、右方陣人數(shù)分別占出操人數(shù)的幾分幾。不知不覺間單位“1”就統(tǒng)一，使原本復(fù)雜的問題轉(zhuǎn)化為十分簡(jiǎn)單的問題，這樣就很容易求出全班的總?cè)藬?shù)：

或

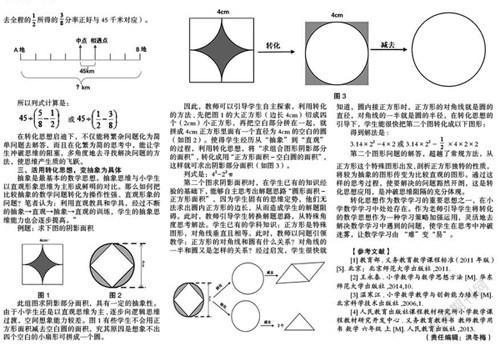
例2：一輛小車從A地到B地要3小時(shí)，一輛大車從B地到A地要5小時(shí)，如果兩車速度不變，同時(shí)從AB兩地出發(fā)，相遇時(shí)過中點(diǎn)45千米，AB兩地相距多少干米？

此題是求兩地的距離，表面上看是行程問題，題目分別給出兩車走完全程所用的時(shí)間，但沒辦法求出小車或大車的速度（每小時(shí)走多少千米？）。學(xué)生拿到題目后，感到無(wú)從入手解題。但運(yùn)用轉(zhuǎn)化的策略，引導(dǎo)學(xué)生把此題的時(shí)間轉(zhuǎn)化成速度，再用分?jǐn)?shù)方法解題，但步數(shù)較多。如：

如果先轉(zhuǎn)化成比，再轉(zhuǎn)化成分?jǐn)?shù)則解題過程和步驟就簡(jiǎn)單很多。如：

小車（3小時(shí)）與大車（5小時(shí)）走完全程所需時(shí)間比是3：5，由于速度不變，在同一時(shí)間內(nèi)，兩車速度的比則是5：3，小車與大車所走路程的比也是5：3。也就是AB兩地的路程共有8份（如上圖），相遇時(shí)小車走了5份，大車走了3份，從A地到中點(diǎn)正好是全程的一半（即），而小車走了全程的，用全程的減去全程的，所得的分率正好與45千米對(duì)應(yīng)（或用全程的減去全程的所得的分率正好與45千米對(duì)應(yīng)）。

所以列式計(jì)算是：

在轉(zhuǎn)化思想啟迪下，不僅能將繁雜問題化為簡(jiǎn)單問題去解答，而且在化繁為簡(jiǎn)的思考中，能讓學(xué)生沖破思維的阻塞，多角度地去尋找解決問題的方法，使思維產(chǎn)生質(zhì)的飛躍。

三、活用轉(zhuǎn)化思想，變抽象為具體

抽象是最基本的數(shù)學(xué)思想。抽象思維與小學(xué)生以直觀形象思維為主形成鮮明的對(duì)比。那么如何把比較抽象的數(shù)學(xué)問題轉(zhuǎn)化為操作性強(qiáng)、直觀形象的問題？筆者認(rèn)為：利用直觀教具和學(xué)具，經(jīng)過不斷的抽象→直觀→抽象→直觀的訓(xùn)練，學(xué)生的抽象思維能力也會(huì)逐步提高。”

例題：求下圖的陰影面積

此組圖求陰影部分面積，具有一定的抽象性。由于小學(xué)生還是以直觀思維為主，逐步向邏輯思維過渡，空間想象能力較差。圖1有些學(xué)生不會(huì)用正方形面積減去空白圓的面積，究其原因是想象不出四個(gè)空白的小扇形可拼成一個(gè)圓。

因此，教師可以引導(dǎo)學(xué)生自主探索，利用轉(zhuǎn)化的方法，先把圖1的大正方形（邊長(zhǎng)4cm）切成四個(gè)（2cm）小正方形，再把空白部分拼在一起，就拼成4cm正方形里面有一個(gè)直徑為4cm的空白的圓（如圖2）。使得學(xué)生經(jīng)歷從“抽象”到“直觀”的過程，利用轉(zhuǎn)化思想，將“求組合圖形陰影部分的面積”，轉(zhuǎn)化成用“正方形面積-空白圓的面積”，這樣就可求出陰影部分面積（如圖3）。

列式是：42-22π

第二個(gè)圖求陰影面積時(shí)，在學(xué)生已有的知識(shí)經(jīng)驗(yàn)的基礎(chǔ)下，能夠自主思考出解題思路“圓形面積-正方形面積”，因?yàn)閷W(xué)生固有的思維定勢(shì)，他們無(wú)法求出圓內(nèi)正方形的邊長(zhǎng)，從而造成學(xué)生的解題阻礙。此時(shí)，教師引導(dǎo)學(xué)生轉(zhuǎn)換解題思路，從特殊角度思考解法。學(xué)生已有的學(xué)科知識(shí)：正方形是特殊圖形，對(duì)角線垂直且相等。此時(shí)，教師以問題引領(lǐng)教學(xué)：正方形的對(duì)角線和圓有什么關(guān)系？對(duì)角線的一半和圓又是怎樣的關(guān)系？經(jīng)過啟發(fā)，學(xué)生很快就知道，圓內(nèi)接正方形時(shí)，正方形的對(duì)角線就是圓的直徑，對(duì)角線的一半就是圓的半徑，在轉(zhuǎn)化思想的引導(dǎo)下，學(xué)生能很快把第二個(gè)圖轉(zhuǎn)化成以下圖形：

得到解法是：

3.14×22 -4×2或3.14×22 - ×4×2×2

第二個(gè)圖形問題的解答，超越了常規(guī)方法，從正方形這個(gè)特殊圖形出發(fā)，剖析正方形獨(dú)特的性質(zhì)，將較為抽象的圖形傳變?yōu)楸容^直觀的圖形。通過這樣的思考過程，使要解決的問題豁然開朗，這是轉(zhuǎn)化思想應(yīng)用，是沖破思維阻隔的充分體現(xiàn)。

轉(zhuǎn)化思想作為數(shù)學(xué)學(xué)習(xí)的重要思想之一，在小學(xué)數(shù)學(xué)學(xué)習(xí)中處處存在。作為老師引導(dǎo)學(xué)生將轉(zhuǎn)化的數(shù)學(xué)思想作為一種學(xué)習(xí)策略加強(qiáng)運(yùn)用，靈活地去解決數(shù)學(xué)學(xué)習(xí)中遇到的問題，使學(xué)生在思考中沖破迷霧，讓數(shù)學(xué)學(xué)習(xí)由 “難”變“易”。

【參考文獻(xiàn)】

[1]教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011 年版）[S].北京：北京師范大學(xué)出版社，2011.

[2]王永春.小學(xué)數(shù)學(xué)與數(shù)學(xué)思想方法[M].華東師范大學(xué)出版社，2014，10.

[3]溫寒江.小學(xué)數(shù)學(xué)教學(xué)與創(chuàng)新能力培養(yǎng)[M].北京科學(xué)技術(shù)出版社，2006，1.

[4]人民教育出版社課程教材研究所小學(xué)數(shù)學(xué)課程教材研究開發(fā)中心.義務(wù)教育教科書 教師教學(xué)用書 數(shù)學(xué) 六年級(jí) 上[M].人民教育出版社，2013.