與拋物線相關的一個定點問題
2022-08-09 10:07:34重慶市銅梁二中402560
中學數學研究(江西) 2022年8期
關鍵詞:拋物線
重慶市銅梁二中 (402560) 李 波 田 飛
圓錐曲線的定點問題中有很多有趣的結論. 筆者發現一個拋物線特有的定點問題,茲介紹如下:
性質如圖1,A(-t,m),B(t,n)分別是直線x=-t,x=t(>0)上的定點,M是拋物線C:y2=2px(p>0)上的動點,直線AM,BM分別與拋物線C交于E,F(E,F存在且不重合),則
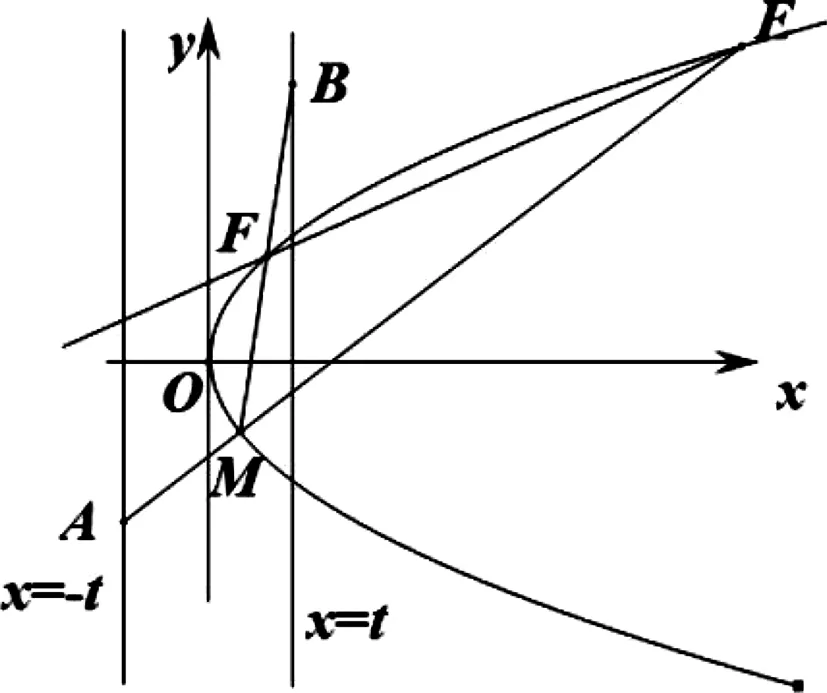
圖1
(1)當m=n=0時,EF是垂直于x軸的動直線;
(2)當m,n中僅有一個為零時,EF恒過定點;
(3)當m,n均非零時,EF恒過定點當且僅當m2n2=4p2t2+2pt(m2-n2).
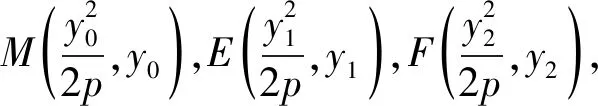
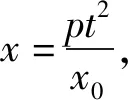
把①式左端看成關于y0的多項式,由于y0具有任意性,可得方程組
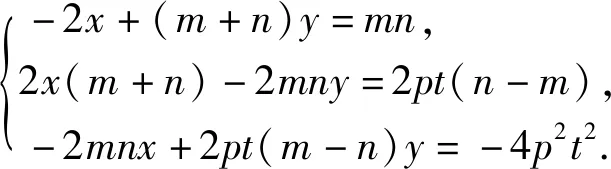
若直線EF過定點,即方程組②有唯一解.
為敘述方便,下面采用線性方程組理論來分析②的解的情況. 非齊次線性方程組②的增廣矩陣
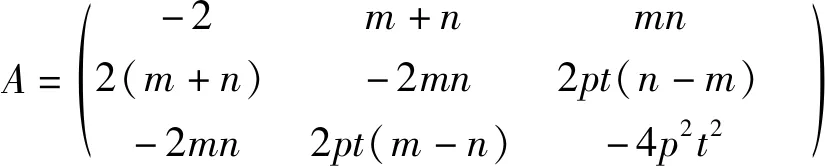
方程組②有唯一解的充要條件是增廣矩陣與系數矩陣的秩都為2,且矩陣的初等行變換不改變矩陣的秩,則m2+n2≠0(即m,n不全為零)且矩陣
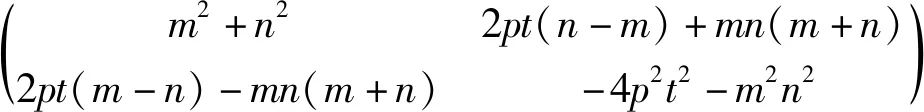
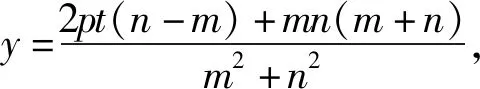
猜你喜歡
中學生數理化·高二版(2025年2期)2025-03-05 00:00:00
語數外學習·高中版上旬(2024年18期)2024-02-20 00:00:00
中學生數理化(高中版.高二數學)(2022年1期)2022-04-26 13:59:58
中學生數理化(高中版.高二數學)(2022年1期)2022-04-26 13:59:56
中學生數理化·中考版(2021年10期)2021-11-22 07:26:38
中學生數理化(高中版.高二數學)(2021年3期)2021-06-09 06:08:40
中學生數理化(高中版.高二數學)(2021年2期)2021-03-19 08:54:12
中學生數理化·中考版(2019年10期)2019-11-25 09:39:04
中學生數理化·中考版(2018年10期)2018-12-07 00:44:42
中學生數理化·中考版(2017年10期)2017-04-23 06:29:38

