小學數學估算教學策略再探
卜俊

摘? 要:
針對學生估算學習中出現的問題,小學階段的估算教學要注意巧設問題情境,如豐富問題情境中的數據信息,將問題情境中確定的數據變為不確定的范圍,從而激發估算需求,培養學生的估算意識;引導充分探索,如嘗試不同的估算方法,選擇合適的估算方法,從而掌握估算方法,提高學生的估算技能。
關鍵詞:小學數學;估算教學;估算意識;估算技能
估算是指根據具體條件以及有關知識,對事物的數量或算式的結果作出大概推斷,給出近似答案。估算對學生數學核心素養的發展有重要的作用:在對數與數量、數量關系以及運算結果的估計中,發展數感與量感;在選擇合適估算方法的過程中,發展推理意識和運算能力;在利用估算結果解釋實際意義的過程中,體會估算在解決實際問題中的作用,形成初步的應用意識。《義務教育數學課程標準(2022年版)》明確提出了小學階段估算的教學要求:“引導學生在具體的問題情境中,選擇合適的單位進行估算,解決實際問題”[1];“借助真實情境,引導學生感悟選擇合適的方法估算的重要性,提高解決問題的能力”[2]。
然而,由于教材中估算內容被分解穿插在各個單元,有些例題和習題的指向也不夠明確,一些教師對估算教學重視不足、定位不準,不少學生估算意識不強、技能欠缺、認知水平不高。對此,筆者提出以下教學策略:
一、巧設問題情境,激發估算需求,培養估算意識
很多學生遇到問題的第一反應是利用精確計算解決,除非題目明確要求估算。也就是說,學生缺乏估算意識,想不到利用估算解決問題。究其原因,除了大量精確計算學習與練習帶來的慣性,主要是學生對估算的價值缺乏深度體驗,沒有真正理解估算的意義。歸根到底,除了生活經驗相對匱乏,也與教師設計的問題情境不足以激發學生估算的需求有關。例如,蘇教版小學數學三年級上冊第一單元《兩、三位數乘一位數》的例2:“西瓜每箱48元,哈密瓜每箱62元,張大叔帶了200元,買4箱西瓜夠不夠?”很多學生覺得精確算出48×4=192并不難,比如可以借助40×4+8×4快速計算,因而不需要利用估算解決。對此,教師在設計問題情境時,要注意讓學生感覺到精確計算很麻煩甚至不可能,而估算很便捷,從而激發估算需求,體驗估算價值,進而培養估算意識。
一方面,可以豐富問題情境中的數據信息,讓學生在處理復雜數據的過程中,感到一一計算費時費力,從而選擇估算。如下面這道題:
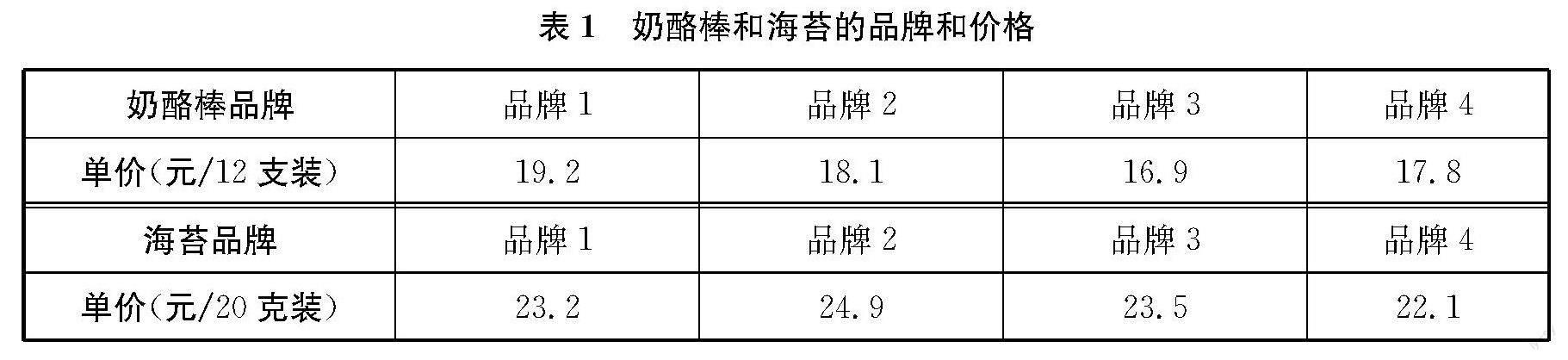
例1? 班級組織春游,樂樂準備購買奶酪棒和海苔在路上吃,她在網上看中了幾個品牌,信息如表1所示。她想買一袋奶酪棒和一袋海苔,大概要帶多少錢?
同樣是購物問題,出示多組數據,學生便能夠感覺到:一個一個去算太麻煩了;同時,要買一袋奶酪棒和一袋海苔,所帶的錢不需要正好,可以多一些,從而可以利用估算解決。
另一方面,可以將問題情境中確定的數據變為不確定的范圍,讓學生因為無法精確計算而選擇估算。如下面這道題:
例2? 學校多功能教室有200個座位。要安排二年級同學在這里開聯歡會,已知二年級有5個班,每班人數在30—40之間,估計一下:夠坐嗎?
把確定的人數改成不確定的范圍,便無法精確計算了。結合“夠坐嗎”的問題,學生自然想到可以用估算的方法,把每個班的人數估計成比較大的40來算。
二、引導充分探索,掌握估算方法,提高估算技能
有時,學生有估算意識,知道要估算,但是缺乏估算技能,不知道如何估算才能解決問題。究其原因,主要是學生沒有掌握估算的方法。歸根到底,是教師沒有引導學生充分探索估算的方法,使得學生沒有認識到方法的本質及其背后的道理。仍以蘇教版小學數學三年級上冊第一單元《兩、三位數乘一位數》的例2為例,對估算的方法,教材直接提示“把48看成50”。這樣,學生不容易認識到方法的本質是“往大湊整”,其背后的道理是“夠多的,一定夠少的;夠少的,不一定夠多的”。實際上,估算的基本原則是確定的,即取好算(好記)的近似值,但是,估算的具體方法具有多樣性[3],需要根據具體問題情境靈活選擇。而且,即使是相同的問題情境,估算的方法也可能不唯一,即具有開放性。因此,教師在教學中,要注意引導學生充分探索,從而真正掌握估算方法,提高估算技能。
一方面,要引導學生嘗試不同的估算方法,感受估算方法的多樣性,積累豐富的估算經驗。以下面這道題為例:
例3? 王大伯把去年收獲的蒜頭裝在同樣大的袋子里,一共裝了6袋。各袋的重量如下頁表2所示,你能估計一下這些蒜頭一共有多重嗎?
在教學過程中,教師要給學生自主嘗試不同估算方法的空間,引導學生發現:可以把每袋蒜頭的重量看成30千克,列式為30×6=180——這種往小估的方法可以稱為“小估法”;可以把每袋蒜頭的重量看成40千克,列式為40×6=240——這種往大估的方法可以稱為“大估法”;可以將各袋蒜頭的重量數字看成與其相近的整十數,列式為40+30+40+30+30+40=210——這種方法就是常見的四舍五入法;可以把每袋蒜頭的重量看成35千克,列式為35×6=210,這種取中間數的方法可以稱為“中估法”;也可以把每袋蒜頭的重量取走30千克,將剩余的重量湊在一起(大約也是30千克),列式為30×7=210——這種方法可以稱為“湊調估法”……
另一方面,要引導學生選擇合適的估算方法,感受問題情境的針對性,提高利用估算解決問題的能力。以下面這道題為例:
例4? (1)400名同學要外出參觀,一共有8輛車,每輛車有56個座位。估算一下:夠不夠坐?
(2)一輛卡車重986千克,運送7箱水果,準備通過一座大橋。每箱水果重365千克,大橋限重4噸,這輛車可以過橋嗎?
第(1)題,單純考慮數據,可以有兩種估算方法:一種是往大估,列式為60×8=480;一種是往小估,列式為50×8=400。對此,教師要引導學生結合問題情境考慮哪一種估算方法合適,從而明確:少的夠,多的一定夠;多的夠,少的不一定夠;保險起見,應該往小估。
第(2)題,單純考慮數據,也可以有兩種估算方法:往大估,列式為1000+7×400=
3800;往小估,列式為900+7×300=3000。對此,教師也要引導學生結合問題情境考慮哪一種估算方法合適,從而明確:多的不超,少的一定不超;少的不超,多的不一定不超;保險起見,應該往大估。
最后需要指出的是,估算具有過程簡單(主要借助內隱的直覺)的優勢和結果粗略、不確定的不足,精確計算具有過程麻煩(主要借助外顯的程序)的不足和結果精準、確定的優勢。“數學認知的發展起始于估算系統,向精確計算系統發展,精確計算系統的發展反過來支持估算系統的發展,它們既有不同的腦機制,又互相支撐、交互發展。”[4]可見,估算和精確計算具有良好的互補性,它們相互協作(靈活選用),能夠提高計算的效率,發展個體的運算能力(包括基于推理選擇合理簡潔的運算策略解決問題的能力)。因此,教師在教學中,不能將估算與精確計算完全割裂開來,而要注意融合估算與精確計算,幫助學生打通兩者的關系,認清兩者的聯系與區別,從而更好地發展運算能力。
參考文獻:
[1][2] 中華人民共和國教育部.義務教育數學課程標準(2022年版)[S].北京:北京師范大學出版社,2022:23,26.
[3] 黃燕紅.估算及其教學策略[J].教育研究與評論(小學教育教學),2022(8):61
62.
[4] 吳增生,李吉寶.數學教學中估算與精算相結合原理初探[J].數學教育學報,2015(5):81.

