基于SOLO分類理論的小學數學習題教學新探索

鮑善軍　鄭書娟

［摘 要］根據SOLO分類理論，學生的數學理解層次從低到高分為五個水平。小學數學習題教學分為發散、關聯和拓展三個階段，以促使學生思維水平按“單點結構—多點結構—關聯結構—抽象拓展”逐步發展至高階思維水平，真正提升學生的問題解決能力，促進學生數學核心素養的內化生長。

［關鍵詞］SOLO分類理論；習題教學；高階思維

［中圖分類號］ G623.5［文獻標識碼］ A［文章編號］ 1007-9068（2023）35-0058-03

一、小學數學習題教學現狀

習題教學不僅有助于學生鞏固知識，而且能夠促進他們形成系統的問題解決方法，并形成高階思維，提高綜合應用知識的能力。然而，筆者發現在實際的習題教學中存在教學內容零散、教學目標浮于表面、教學活動單一等問題。

首先，教學內容零散。習題之間缺少邏輯關系和系統性，教學時只有一連串的講解和練習，忽略了習題間的內在關系。對于簡單的習題學生完成后教師直接批改，而對于稍微復雜的習題教師則反復強調，處理得過于細致。

其次，教學目標浮于表面。在講解習題時，教師往往只關注問題本身，沒有充分利用素材進行深入講解。教學只在解決問題的表面徘徊，忽視了高層次思維能力的提升。過分強調解題技巧，而未能深入探討問題的本質，也忽視了學生分析、聯想和抽象思維能力的培養。

最后，教學活動單一。未能發掘習題背后的深層價值，學習活動缺少探究和發現的環節。過分關注問題的結果，導致學生在解題和訂正的過程中反反復復，沒有數學思維和解題經驗的提升。

二、基于SOLO分類理論的習題教學架構

依據曹培英老師的觀點，基于SOLO分類理論及可觀察的學習結果，學生數學理解層次從低到高可分為前結構水平、單點結構水平、多點結構水平、關聯結構水平和抽象拓展結構水平。

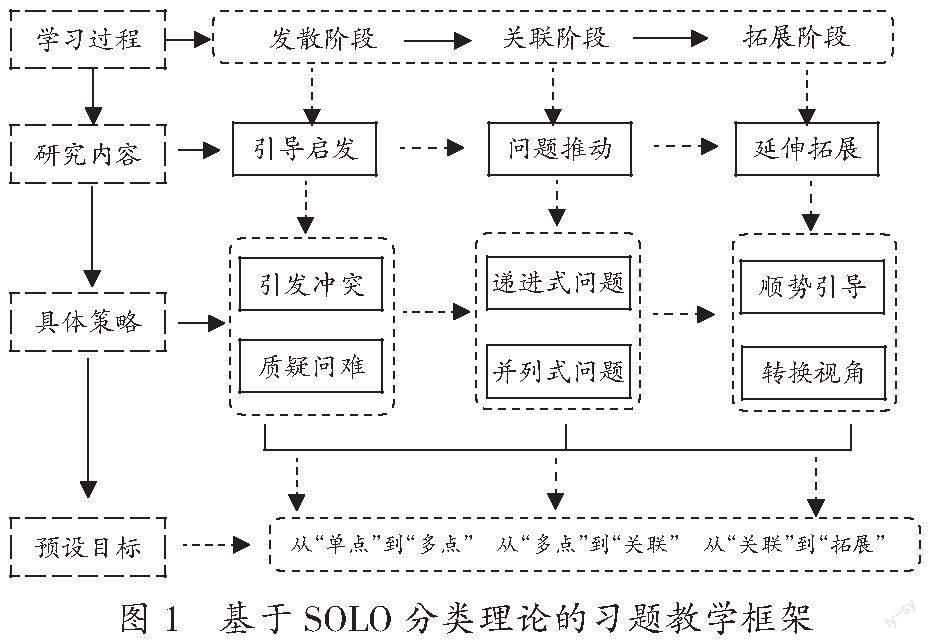
基于SOLO分類理論，習題教學分為發散、關聯和拓展三個階段（如圖1），通過梯度化呈現，促進學生對知識之間的關聯性的理解，實現“學一題、透一點、通一類”的學習目標；通過進階式教學，引領學生積累問題解決的經驗，發展數學核心素養。

三、基于SOLO分類理論的習題教學策略

1.引導啟發：思維水平從“單點結構”走向“多點結構”

學生的思維活動是帶有明顯主觀傾向的情意認知過程，教師教學時需要給予學生熟悉且具有引導性的啟發，來促進他們從不同角度思考問題，用不同路徑解決問題。

（1）引發沖突，以劣構性問題激活思維因子

從學生的認知經驗入手，以劣構性問題使學生處于“悱憤”狀態。將原有題目進行改編，刪減或增加條件，激發學生思考，從而促進學生在解題的過程中發展多樣化的認知。

【案例1】改編問題“張老師花48元買6本同樣的筆記本，每本筆記本多少元？”

給出條件不足的問題“張老師花48元買同樣的筆記本，每本筆記本多少元？”，讓學生在此基礎上增加合適的條件，并解決問題。學生提出的問題有“張老師花48元買2本同樣的筆記本，每本筆記本多少元？”“張老師花48元買2本同樣的筆記本，還剩8元，每本筆記本多少元？”。

教師也可以增加條件，得到新問題 “在文具店，張老師花了48元，李老師買6盒鉛筆所花的錢比張老師花的錢多12元，每盒鉛筆多少元？”

通過補充條件并解決問題，激發學生思維，促使學生主動思考、分析，考慮多方位知識，將相關的知識進行整合，促進學生多元認知。

在補充條件的過程中，學生需要將知識有效地組合在一起。這樣可以激發學生的思維潛能，促使他們積極地思考和分析，并將相關的知識聯系起來進行整合，推動學生認知的多元化并深化思考。

（2）質疑問難，以開放性問題點燃思維火花

教師要給學生提供質疑問難的空間，引導學生自我提問并解決問題，使學生在反思中主動探究。探究的問題應具有開放性，促進學生思維不斷發散，從不同路徑去思考或解決問題，促進思維的多點提升。

【案例2】教學“多邊形內角和”

教師提出問題“三角形內角和是180°，四邊形內角和是多少度呢？”，讓學生動手畫四邊形并求所畫四邊形的內角和。學生完成后，引導學生研究五邊形、六邊形、七邊形等，從中發現規律。然后，用問題“有一個五邊形，沿直線剪一刀剪去一個角，得到一個新多邊形，可以怎么剪，新多邊形的內角和可能是多少？”激發學生的創造性思維。

用“多邊形的內角和怎么計算”“五邊形剪去一個角，得到的多邊形內角和可能是多少”等開放性問題，促使學生多角度思考，形成多元認知。

2.問題推動：思維水平從“多點結構”邁入“關聯結構”

將若干個核心問題組成遞進式問題鏈，能串聯知識脈絡，將學生的思維引向深處；組成并列式問題鏈，能拓展學生思維，促進學生思維的發散，驅動學生自主思考、探究和表達，使得學生對已有經驗形成結構化認知，重新建立知識體系。

（1）遞進式問題，將學生思維引向深處

以數學核心知識為統領，充分挖掘習題背后的數學思想，并通過遞進式問題鏈關聯知識脈絡，促使學生經歷知識串聯、問題解決的過程，發展學生的數學思維。

【案例3】教學“長方形面積和周長的關系”

問題1：用24米長的線段圍成一個長方形，能怎么圍？

問題2：畫出你想到的長方形，計算面積并觀察，長方形面積有什么變化規律？

問題3：為什么會有這樣的規律？

教學“長方形面積和周長的關系”時，教師需要創設具體情境，并挖掘涉及的知識點及其價值，以設計問題鏈引導學生探索周長相等情況下面積的變化規律。案例中的三個問題層層深入，引導學生串聯長方形周長和面積知識，整體建構，使學生的思維向縱深發展。

（2）并列式問題，使學生思維更廣闊

條理清晰的思維建立在結構化的知識之上。利用一系列問題喚起學生對知識的記憶，并通過比較、總結和抽象等思維活動將這些知識結合起來，有助于學生構建知識體系。這種方法不僅能促進學生在學習同一主題的不同內容或方法上對知識的理解與融合，而且還能拓寬學生的思維。

【案例4】習題“籠子里有若干只雞和兔，一共 8 個頭、22 條腿，雞和兔各有幾只？”

問題1：用表格能列出所有情況嗎？

問題2：用畫圖的形式能將題意表示清楚嗎？

問題3：你能根據所畫的圖列出算式嗎？

問題4：這些方法有什么聯系嗎？

這幾個問題能促使學生借助三種方法進行探究，促進深度思考和理解，從而融會貫通方法，還能拓寬思維。

3.延伸拓展：思維水平從“關聯結構”躍至“抽象拓展”

具有創意性的聯想和問題解決策略，對學生認識、理解和重構知識大有裨益。教師要指引學生沿著已有的知識脈絡去類比和推廣，且轉變不同的思考視角，進一步提出衍生問題。這種方法能鼓勵學生跳出常規的思維模式，從而延展思維的“長度”，使得他們的思維觸角能夠向更遠處伸展。

（1）順勢引導，以拓展性問題拓寬視野

學生能否在探究、拓展與發現等學習活動中打破原有認知，重建知識體系，關鍵在于問題的設計及學生是否具有審辨式思維。因此，教師要設計拓展性問題，以引導學生發現新知，拓寬視野。

【案例5】教學“平均數的再認識”

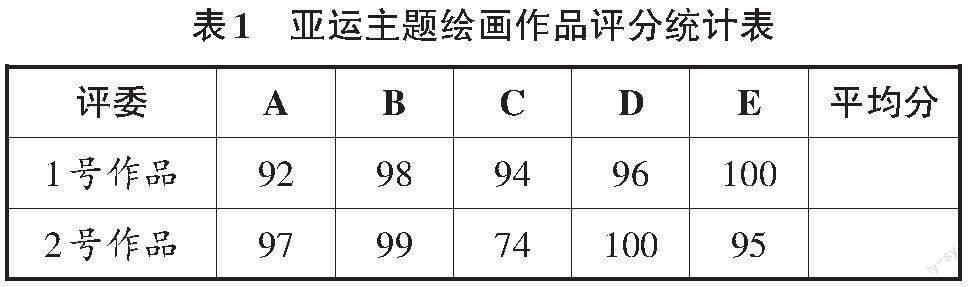
教師出示表1，并提問：“表中是五位評委對亞運主題繪畫作品的評分。根據評分，哪幅作品勝出？”

若學生回答1號作品，教師可引導：“作品2的平均分被評委C的74分拉低了，直接算平均數的評價方法失之偏頗，去掉極端數據后再計算平均數似乎更合理。”接著以圖說理，通過多媒體直觀呈現平均數受到極端數據影響的變化，使學生體會平均數的敏感性，明白“計算平均分時去掉一個最高分和一個最低分”的原因，促進學生對平均數的合理選擇與靈活應用。

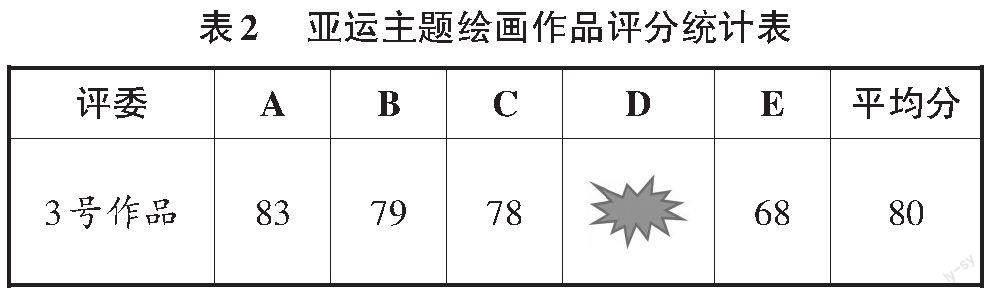
教師接著出示3號作品的評分統計表（見表2）并提問：“評委D的評分不小心被墨汁覆蓋了。想一想，已知去掉一個最高分和去掉一個最低分后，平均分是80分，滿分是100分，評委D可能打了多少分？①92；②83;③75;④100；⑤88。”

學生在探究與思辨中發現要分“D打的分既不是最高分，也不是最低分”“D打的分是最高分”“D打的分是最低分”三種情況來分析。

最后，教師呈現生活中的實際問題，引導學生思考“平均數是唯一的評判標準嗎”“是否還存在其他統計量”等問題。

“平均數的再認識” 的教學目標是加深學生對平均數的認識，特別是在主觀評分的場景中加深計算和原理的理解。通過思考“哪幅作品勝出”或“評委D可能打了多少分”等問題，學生不僅鞏固了計算平均數的技能，而且學會了在逆向推理時考慮去除了極端值的情況。鼓勵學生大膽提問和質疑，使他們打破對平均數的傳統理解，認識到平均分并非衡量一組數據的唯一標準，擴展了他們對數據分析的認識。

（2）轉換視角，以破勢性問題打破思維定式

學生初步建立的知識結構常常是順向的、固定的，缺乏靈活性、動態性。針對認知經驗設計破勢性問題，有助于學生轉換思考視角，打破思維定式，另辟蹊徑，創造性地解決問題，實現數學思維的再延伸。

【案例6】教學“長方形周長與長、寬的關系”

教師讓學生探究問題“用16張邊長為1分米的小正方形拼長方形，怎么拼才能使拼出的長方形周長最短？”，學生得到長方形長和寬的長度分別是1分米和16分米、2分米和8分米、4分米和4分米（正方形），對應的周長分別是34分米、20分米和16分米，其中，拼成正方形時周長最短。

教師接著利用問題“如果用36個小正方形去拼呢？”引導學生有序思考。學生用表格記錄（見表3），發現還是拼成正方形周長最短，驗證了規律，鞏固了認知。

教師提問：“1個正方形可以平均分成3個周長都是8厘米的長方形，原來正方形的周長是多少？”學生按照正方形周長公式計算，教師追問是否有其他方法，并把條件轉化成“用三個周長是8厘米的長方形拼成一個正方形”，引導學生從另一個角度去思考問題，有利于學生打破思維定式，實現思維的再生長。

這幾個問題涉及周長的變化規律，讓學生在解決問題的過程中鞏固認知、提升能力。

實踐證明，基于SOLO分類理論的習題教學能幫助學生學會用聯系的觀點思考問題，積累解決問題的思維經驗，形成優良的認知結構。一線教師只有持續研究與實踐，方能通過習題教學逐步發展學生的高階思維水平，真正提升學生的問題解決能力。

［ 參 考 文 獻 ］

[1] 彼格斯，科利斯.學習質量評價：SOLO分類理論（可觀察的學習成果結構）［M］.高凌飚，張洪巖主譯.北京：人民教育出版社，2010.

[2] 鮑善軍，朱曙光.“一題一課”的教學價值、設計與策略[J].教學月刊小學版（數學），2022（Z2）：12-16.

[3] 鮑善軍，朱曙光.基于SOLO分類理論的“一題一課”教學設計與實踐[J].教學月刊小學版（數學），2021（11）：35-39.

[4] 鄭書娟.放大過程，讓思維向更深處漫溯：三年級“拼圖與周長”教學實踐與思考[J].小學教學參考，2021（23）：55-56.