數學作業的創新設計

閆穎

摘要：作業是檢測學生學習情況的重要方式，作業設計應基于素養立意。據此，創新設計作業內容、形式和評價。作業內容應深耕教材，追求練活、夯實和延展；作業形式應彰顯理趣，嘗試變式、統整和薦題；作業評價應體現多元，關注素養、過程和生評。

關鍵詞：小學數學；作業設計；核心素養

作業是檢測學生學習情況的重要方式。隨著“雙減”政策的深入推進，特別是《義務教育數學課程標準（2022年版）》的實施，設計發展數學核心素養的作業成為應然追求。素養立意的小學數學作業設計在內容、形式和評價等方面，既要守正，又要創新。下面，圍繞作業內容、作業形式和作業評價三個方面，談談小學數學作業的創新設計。

一、創新作業內容：深耕教材，追求練活、夯實和延展

數學教材中的習題是數學作業內容的重要來源。數學作業內容的設計，應當深耕教材，用好基礎題、操作題和思考題。

（一）練活基礎題

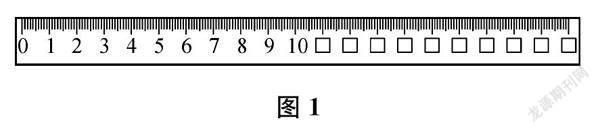
教材中的基礎性練習題一般是鞏固基礎知識和基本技能的載體，對于基礎題要追求練活。例如，蘇教版小學數學一年級上冊《認識11～20各數》單元，在“想想做做”中安排了這樣一道練習題：看著尺子上的數，從0讀到20。本課的作業以此題為素材，設計如下：

第一層次——填數。對直尺圖做加工處理（見圖1），讓學生自主填一填。這樣的處理，打破了原來封閉的完整“數尺”結構，給學生填數的機會，通過填數，整理本課學習的內容；同時，將新知納入原有的認數范圍，利于學生形成完整的認知結構。

第二層次——讀數。先從左往右讀再從右往左讀，接下來跳著讀：2個2個讀，體會單數和雙數；3個3個讀、5個5個讀，發展數感，培養思維的靈活性，同時滲透乘法口訣。如此，以讀的方式帶動思維發展，避免簡單的背誦式唱讀。

第三層次——比較。讓學生在數尺上先找出比10大的數，再找出比10小的數，最后說一說“7和12哪個更接近10”，從而使學生體會到：數線上，越向左，數越小；越向右，數越大。

第四層次——猜數。借助數尺，讓學生按提示開展猜數活動。例如，從6開始向右數3個數，數到幾，再向左數3個數，數到幾；從16開始向左數3個數，數到幾，向右數3個數，數到幾；從16開始，向右數5個數，數到幾。這樣層層推進，不僅能夠發展學生的數感，讓其體會數序，還能夠滲透加法、減法的本質。

此項作業設計，教師借助“數尺”直觀，將認數、數數、運算的意義、數的本質等有機融合，能夠發展學生的數感、空間觀念，鍛煉運算能力和推理能力，避免練習在淺層次思維上的簡單重復，真正實現為素養賦能。

（二）夯實操作題

利用教材中的操作題，設計體驗式、實踐性的作業，可讓學生在操作中體驗數學、內化新知、解決問題。例如，蘇教版小學數學四年級上冊《認識升和毫升》單元，安排了“動手做”活動。活動目的有二：一是讓學生使用自己制作的量器，體驗這樣的量器也是計量“水”有多少的工具；二是讓學生繼續體會1升水有多少，豐富對“1升”的感知。這樣的活動，教師往往作為家庭作業布置給學生，然后就“再無下文”了。這其實浪費了一次發展素養的機會。筆者對這一“動手做”做了“長遠規劃”：為學生提供學習單，利用任務驅動，促進學生互動交流、運用拓展。“動手做”作業單內容如下：

1.做一做：按要求制作一個量器。材料：上、下一樣粗的瓶子一個，黑線筆一支，量杯一個。

2.量一量：找出幾種不同的容器，把1升水倒進去，看看水面在哪里？思考：你有什么發現？

3.估一估：估計這幾種容器的容量，再動手驗證。

有了任務驅動，學生能夠充分展開觀察、閱讀、操作、嘗試、計算。同時，把交流的時間還給學生，并展評學生的實踐作業單，設置“過關”小游戲。以“過關”促學習、促交流、促實踐，拉長操作型作業的時效性。

（三）延展思考題

為了更好地培養學生思維的連貫性和持續性，我們要延展教材中思考題的內容。例如，蘇教版小學數學四年級下冊《三位數乘兩位數》單元呈現了一道思考題：“用0、1、2、3、4這五個數字組成一個兩位數和一個三位數，要使乘積最大，應是哪兩個數？要使乘積最小呢？換五個數字，再試一試。”單純放手讓學生嘗試，多數學生就是組成幾個數試一試。大量的計算并不利于學生思維的發展。對此，教師以此題為作業基點，精心設計了5個探索活動：（1）嘗試。兩個數的和是9，這兩個數各是幾時，它們的乘積最大？（學生嘗試解決并發現——兩個數的和一定，這兩個數越接近，積就越大；反之，這兩個數差越大，積就越小。）（2）思考。去掉最小的0，用1、2、3、4這四個數字組成盡可能大的兩個兩位數，則它們的十位上應該是（）和（），個位上應該是（）和（），它們可能是（）和（），或（）和（）；要使它們的積最大，根據兩個數越接近，積就越大，判斷它們應該是（）和（）。（3）推理。用0、1、2、3、4這五個數字組成的三位數乘兩位數，積最大是（）和（）。（4）類比。用0、1、2、3、4這五個數字組成積最小的三位數乘兩位數。（5）變式。換5個數字試一試。這樣的探究性作業，讓學生“跳一跳，摘桃子”，真正讓思考有跡可循。

二、創新作業形式：彰顯理趣，嘗試變式、統整和薦題

數學作業的形式應彰顯理性與趣味，通過變式、統整、薦題等，促進學生內在經驗的不斷豐富和數學思維的不斷提升。

（一）變式：一圖數變

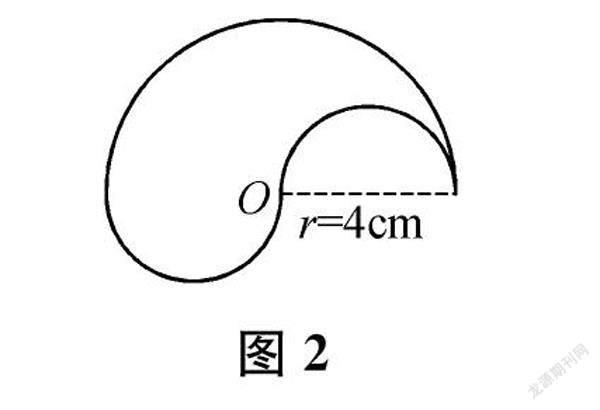
變式是創新作業形式的常見方法。例如，蘇教版小學數學五年級下冊第110頁第9題“計算圖形周長”第2小題（見圖2）的常規解法有三種：（1）求出三個半圓的周長再相加；（2）把兩個小半圓看成一個圓，計算后再相加；（3）直接求出一個大圓的周長。這三種方法體現了學生不同層次的思維水平。

基于以上分析，筆者通過多次變式，設計了多個層次的作業：

第一層次：自主嘗試，選擇算法。讓學生用不同方法嘗試解決，然后思考哪種更簡便。使學生明確，用轉化的方法，即把三個半圓的周長轉化成一個大圓的周長是最簡便的，初步感受轉化策略的價值。

第二層次：變化數據，體會聯系。原圖不變，變化圖中數據：如果圖中r=4 cm改為r=6 cm和r=8 cm，你能計算圖形的周長嗎？解決后與原題比較，說說有什么發現。意在讓學生體會：雖然數據發生了變化，但圖形沒變，解題的方法也是相同的，也可以轉化成一個大圓的周長進行計算。

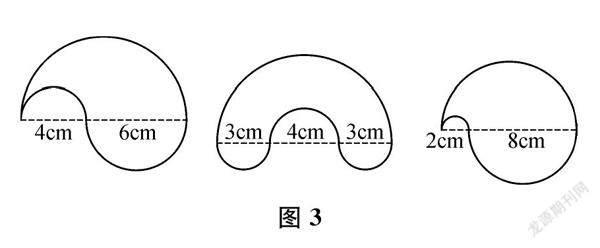
第三層次：圖形變換，求同辨異。觀察圖3的三幅圖，猜測每幅圖的周長可以怎樣算，再嘗試計算，思考有什么發現？進而明確：雖然圖形發生了變化，但計算的方法沒變。這個層次，從解決一個問題上升到解決一類問題，在不同中感悟相同。

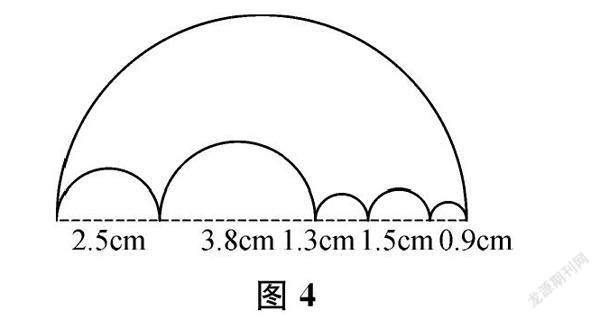
第四層次：大膽改圖，反思質疑。結合上面的研究經驗大膽設計一幅圖（比如圖4），要求：周長的計算方法和前面圖形一樣。通過開放的圖形設計，使學生體會到，圖形無論如何變化，都能夠用“直徑×π”來直接計算圖形的周長，從而將經驗上升到思維的層面，在感受轉化策略的同時，發展直覺思維、形象思維和邏輯思維。

這項作業以教材中的一幅圖為素材，通過不斷變式、對比，讓學生在猜測、計算、比較、發現中經歷一次次思維的高峰體驗。在這樣的體驗中，學生通過一次次異中求同、同中求異，感受數學“變與不變”的辯證之美，數學思維也逐步走向深刻。

（二）統整：多圖同用

教材上的練習題有一定連續性，在梳理和對比的基礎上進行統整，能找到知識間的聯系和區別，從而形成知識板塊。例如，教學蘇教版小學數學五年級下冊《圓》單元后，組織學生從教材中找出相似的組合圖形。經過梳理，學生找到與第 91頁第13題的圖類似的5幅圖，分別在第92頁的例5，第102頁“練習與應用”的第2題、第12題以及第114頁《整理與復習》的第22題中。這些題圖形相似，但解決的問題、方法各不相同。這樣的梳理有利于學生溝通知識之間的聯系，將原有的知識進行整合和重組，通過分析、比較、綜合和歸納發展直覺思維和推理能力。

（三）薦題：學生自薦

教師還可嘗試讓學生自主推薦“好題”，并說明推薦的理由。例如，學完蘇教版小學數學五年級上冊《小數加法和減法》單元后，學生推薦的題目為：“麗麗在用豎式計算4.52加一個一位小數時，錯把末尾對齊，得數為4.73，這個加法算式的正確結果是多少？”推薦的理由是：“多數同學無從下手；末尾對齊和小數點對齊的差別值得思考。”通過對推薦題的再思考、再交流，學生經歷發現錯誤、順應錯誤、找出關鍵、修正錯誤的過程，在“將錯就錯”中找到問題的突破口，同時還出現了很多個性化的解題方法。教師每天從學生推薦的題目中選擇有思維價值的“好題”推薦給全班。這樣的作業，“取之于生，用之于生”，利于學生不斷思考、解答、對比、篩選。

三、創新作業評價：體現多元，關注素養、過程和生評

數學作業評價要體現多元，既關注知識技能、作業結果、教師評價，更關注核心素養、作業過程和學生評價。

（一）關注知識技能，更關注核心素養

面對學生在同一知識點、能力點處一錯再錯的情況，教師大多會用重復練習的方式幫助鞏固。但要從根源上解決問題，教師需要在關注知識技能的同時更關注核心素養，基于素養立意評價作業。例如，教學蘇教版小學數學四年級下冊《乘法分配律》單元后，教師安排了一道開放題：“要使76×A+39×B能用乘法分配律簡便計算，如果A=61，那么B是（）。”學生的答案有兩種情況：一種是61，因為乘法分配律中有一個因數是一樣的；另一種是76，因為不僅有一個因數是一樣的，而且39和61可以湊成整百數。從知識技能的角度來看，兩種方法都是正確的，都具備乘法分配律的模型。但從核心素養的角度來看，顯然第二種方法的思維含量更高。運算律的重要價值是使計算更簡便，提高準確度。思考的過程中，學生的思維變得更有邏輯性，更加嚴密。這有利于學生推理能力的發展。

（二）關注作業結果，更關注作業過程

比起作業結果，作業過程更重要。只有過程是正確的，才能保證結果的正確性。過程更能看出學生思考的痕跡，洞察學生的真實水平。例如，對于拓展性作業中的一道簡便計算題“1+2+3+4+…+50”，學生中出現了幾種答案：1249、1250、1275。典型的作業過程有這樣幾種：第一種，1+2+3+4+…+50=（1+50）×24+25=1224+25=1249；第二種，1+2+3+4+…+50=（24×50）+50=1200+50=1250；第三種，1+2+3+4+…+50=（50+1）×25=51×25=1275；第四種，1+2+3+4+…+50=（1+49）×24+50+25=50×24+50+25=50×25+25=1250+25=1275。從這些解答過程中可以看出，學生的思維水平是不一致的，但都想到了兩個數結合在一起。如果只關注結果，忽視學生的做題過程，就會錯失“看見”思維的機會。對于過程準確、結果正確的兩種情況，都予以肯定，引導學生觀察、比較每一步背后隱藏的依據；對于前兩種錯誤的情況，引導學生分析計算過程中合理的成分，修正不合理的成分，給予相應的評價。

（三）關注教師評價，更關注學生評價

作業評價應引導學生主動參與，提高學生自我評價、自我反思的能力。要讓每位學生在教師評價后面寫出自己的反思和對策，包括錯誤原因，是否需要教師、同學幫助，自己做題中的合理成分與閃光點等，化被動為主動，避免二次出錯。最后，教師進行總結評價，鼓勵學生交流，激發他們學習數學的熱情。同時，站在學生的立場縱橫比較，為學生個體的素養提升“謀篇布局”。