適時追問，培養學生思維

劉瑞文

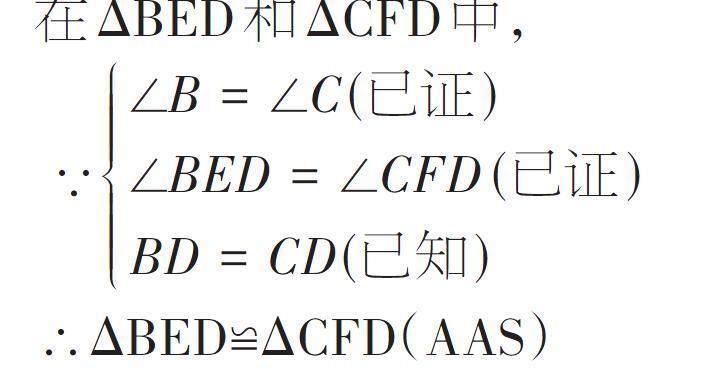
摘要：近日，教育部發布了2022年版義務教育課程方案和課程標準修訂情況。新課標聚焦發展學生的核心素養，對重大主題教育進行了整體規劃和系統安排。讓核心素養落地，是本次課程標準修訂的工作重點。

關鍵詞：課堂教學? 核心素養? 思維培養

學生的素養發展，貫穿新課標全文本，隱含在課程內容及教學實踐中，體現在課程學習結果的具體描述中。例如，數學學科提出應培養學生具有如下素養：會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界，簡稱為“三會”。

如何在自己的課堂中將落實核心素養與課堂基本知識傳授相結合，是每個數學教師應該深度思考的問題。數學課一直給人的印象就是抽象難懂，枯燥乏味的，盡管現在很多農村學校都安裝了電子白板，借助多媒體進行教學后，我們的數學課堂變得更直觀了，更有活力。對于初中學生而言，我覺得第一“會”不難做到，難的是后面“兩會”，所以教師在平時的教學中要有意識地引導學生朝這兩方面來發展。

結合平時教學中的經歷，我發現在課堂中有效的追問能提高學生的學習能力，能夠讓學生在發生錯誤時迷途知返，能夠在學生理解重難點處畫龍點睛。追問運用得當，對于學生明確自己的想法，提高學生思維活動的完整性和準確度有很大幫助。以下是我在教學中對追問的一些實踐與探索。

一、在意外之處追問

葉瀾老師說：“課堂應是向未知方向挺進的旅程，隨時都有可能發現意外的通道和美麗的風景，而不是一切都必須遵循固定的路線而沒有激情的旅程。”如下試題：

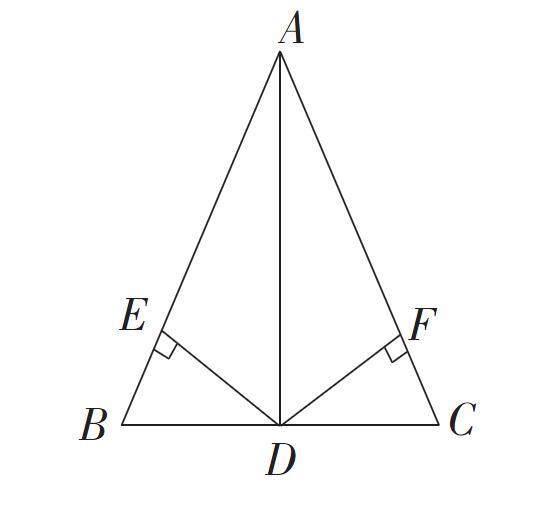
在ΔABC中，AB=AC ， BD=DC，DE⊥AB，DF⊥AC，那么DE與DF相等嗎？說明理由。

本來我是預設學生利用剛學到的三角形全等的條件 來證明的，讓學生思考片刻后，我請一位學生上臺寫出他的證明過程：

解：∵AB=AC ，BD=DC

∴∠BAD=∠CAD

∵DE⊥AB，DF⊥AC

∴DE=DF

這位學生的證明出乎我的意料，因為他用的是我還沒有講到的知識來證明的，所以我非常高興地表揚了這位學生超前學習的能力，然后我在這位學生的每個解題步驟后面都加上一個括號，變成了以下這樣：

解：∵AB=AC ，BD=DC（? ? ?）

∴∠BAD=∠CAD（? ? ? ? ? ? ）

∵DE⊥AB，DF⊥AC（? ? ? ? ?）

∴DE=DF（? ? ? ? ? ? ? ? ?）

讓他把每一步的依據也備注在括號里，了讓其他的學生感受一下他的解題思路。接著繼續發問：“有誰用其它方法證明的嗎？”我從舉手的部分學生里又叫了一位學生上來解題，具體步驟如下：

解：∵AB=AC （已知）

∴∠B=∠C（等腰三角形兩底角相等）

∵DE⊥AB，DF⊥AC（已知）

∴∠BED=∠CFD（垂直的定義）

在ΔBED和ΔCFD中，

∵[∠B=∠C（已證）∠BED=∠CFD （已證）BD=CD（已知）]

∴ΔBED≌ΔCFD（AAS）

這樣一來，既讓臺下的學生體會到兩種思維方式的特點，也為他們后面的學習做了一下熱身，可謂一舉兩得。

課堂教學隨時會有出乎教師意料之外的情況發生，如果教師總是按照自己的教學計劃來組織教學環節，就會無形中束縛了學生們的發散性思維，不利于培養學生的創新思維。因此我們對于學生的“意外表現”，要積極回應和主動追問，激活學生思維，拓展想象空間，讓教學中的“節外生枝 ”演繹出獨特的價值。

二、在出現錯誤之處追問

學生在課堂中出現一些差錯是不足為奇的，當我們遇到這種情況時不應以一個“錯”字責備學生，更不要直接說出正確答案，而應該正確解讀學生的錯誤，弄清楚產生錯誤的原因，再把握合理的糾錯時機，通過追問的語氣和角度來引導學生片面的解讀，讓學生自己意識到錯誤并且糾正。

例如，在講到“相遇問題”時，進行如下試題時：

甲乙兩地相距720千米，兩車同時從甲乙兩地相向開出，甲車速度是100Km/h，乙車速度是80Km/h，求幾小時后兩車相遇？

學生在求解過程出現了兩種列式：

（1）720÷（100+80）

（2）720÷100+720÷80

針對這兩種情況，我沒有說明誰對誰錯，追問學生：“你們覺得哪種列式才是對的呢？同意第一種解法的舉一下手，認同第二種解法的舉一下手。”結果有一部分學生沒舉手，“那些沒舉手的學生是認為兩種都對還是有不同看法？”然后讓沒舉手的那部分學生把兩種解法的答案求出來。當他們發現得數不同時，我繼續追問：“得數怎么會不一樣呢？是不是算錯了？”學生通過驗算發現計算沒錯，那問題出在哪里呢？我又從認同第二種解法的學生中選出一名代表，“給大家說一下你這樣列式的思路吧。”學生說：“因為利用分配律，720÷（100+80）可以轉化為720÷100+720÷80， 所以我就列出這個式子了。”聽到“分配律”一詞，我就知道知道學生出錯的原因了，順著這個“癥結”，我繼續發問：“請大家回憶一下，你們學過的分配律是在哪種運算當中出現的？”“乘法分配律。”學生異口同聲回答。“有沒有除法分配律？”“沒有。”

如果教師一開始就對“720÷100+720÷80”這種算式“一錯而過”，置之不理，就不會出現“百家爭鳴”的場面。因此，在學生的錯誤之處適時地追問，可以讓學生有更多的機會闡述自己的想法，讓學生領著學生們去探究錯誤產生的原因，比起教師直接向學生解釋正確答案，效果真是好太多了。

三、在缺乏深度之處追問

七年級學生在學習過程中，很多時候對問題的思考都只是停留 在片面，這時教師要有意識地追問和引導，搭設思維跳板，幫助學生開拓思路。

例如，在講到“相交線和平行線”的內容時，設計如下試題：

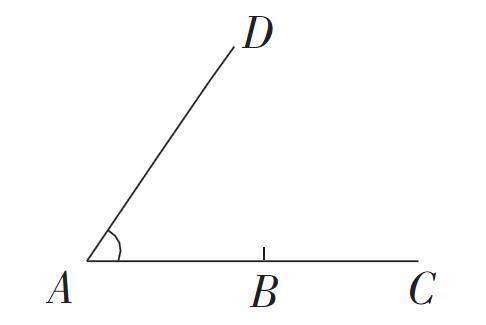
如圖，以點B為頂點，射線BC 為一邊，利用尺規作∠EBC，使得∠EBC=∠A，EB與AD一定平行嗎？

在講解這道題之前，我讓學生們先在課本上作圖，在巡視過程中發現多數學生只畫出了一種情況，于是我叫了一位學生上黑板來畫，他的圖是這樣的：

我首先肯定了這位學生的做法，并問：“如何判定AD//BE呢？”“因為∠DAB等于∠EBC，根據同位角相等，兩直線平行可以得到AD//BE。”學生回答。

我又問：“請大家仔細觀察一下原圖，以B點為頂點，以射線BC為一邊的角只有一個嗎？”過了一會兒，有人回答：“可以把BE邊畫在BC邊下方！”一石激起千層浪，臺下的學生恍然大悟，紛紛畫出了第二種情況的圖形：

從第二個圖形可以很直觀地看出，AD不會跟BE平行。因此，在學生思考欠缺深度時，通過一環扣一環的追問，引導學生將問題一層層剝開，使其知其然，又能知其所以然。這對于引發學生自主探究，提高學生思維的敏捷性和深刻性，構建完整的知識體系具有關鍵的作用。

在實際教學中，促進學生核心素養的方式有很多，不同的老師有不同的方法，但“追問”應該是每位教師在每一節課上都能用到的，課堂中的追問是教師教學智慧和教學藝術的體現，是促進學習氛圍的催化劑。適時的追問開啟了學生思維的閥門，可以為學生在自主探究活動中“跑偏了”的時候拉一把，既提升了教學質量，又演繹了課堂的精彩。

總之，課堂是學校教育中核心素養能否真正落地的關鍵環節，教師們首先要用核心素養更新自己的教育理念，才能提高教育教學質量，進而促進學生核心素養的發展。