小學數學概念教學策略研究

鄺儒軍

【摘要】概念是數學的基石，小學數學教學的重要組成部分之一就是概念教學；怎樣才能使小學生明白這些既具備抽象性又具備概括性的數學概念，對于廣大數學教師來說都不是一件輕松的事情，主要矛盾就在于小學生的認知水平不足、生活經驗還不夠豐富、邏輯思維能力比較弱.基于此，文章根據筆者自身的教學體會，給出了相關問題的一些解決的方式與策略，以期為一線教學工作者提供參考.

【關鍵詞】概念教學；數學實踐；圖形化；等式性質

引 言

概念意味著抽象性高、概括性強.小學生因為年齡與認知的限制，對抽象的、概括性的事物理解起來就比較費力，而對形象的、具體的事物則容易接受.從這個角度來看來，必須把概念性的東西具體化與形象化，首先得讓學生感受得到，讓他們有一個感知的過程；其次進行概括、提升到概念階段，在這一階段發展出概念的一般性質，最后回到具體的事物當中，對在概念階段發展出來的性質做進一步的應用.

思維品質包括思維的敏捷性、靈活性、深刻性、獨創性和批判性.其中深刻性是一切思維品質的基礎.對數學概念的理解往往需要抽象思維能力與邏輯推理能力，而這與小學生的知識結構體系以及其認知水平之間存在著很大差異，所以教師在概念教學時，需要注意以下幾個方面.

一、理解概念形成的過程

數學概念具有很強的抽象性，小學生的思維主要以具體形象思維為主，所以在引入概念時就要循序漸進，放慢節奏讓學生初步理解概念.小學生受生活經驗與認識水平的限制，對于一個新的概念，總是有一個形成過程，通常是需要反復直觀地感受、在教師地指導下進行總結、歸納，循序漸進地形成，不可一蹴而就.

例如，在第一次學習“解簡易方程”時，就必須得讓學生充分地經歷探索等式的性質這一過程，如等式：3×5-4×2=2×3+1.探索等式的性質，可進行如下三種操作：

化簡可得5x=15.再進行第2種操作，兩邊同時除以5，就可以得到x=3.

一些教師忽視了這一過程，只求簡單高效，直接讓學生背誦等式的性質，再去做大量的練習.只是教學生怎么做，而忽略解方程所蘊含的數學思想與方法.這樣就容易造成學生只會機械地做題，沒有弄明白為什么要這樣做，無法體會到各個知識之間的內在聯系.

二、概念之間的聯系

新舊概念之間通常不是孤立存在的，有著緊密的聯系.對新概念的理解往往需要以舊概念為前提或基礎，可以認為是舊概念的“推廣”；新的概念大都也是從舊概念發展而來.所以，在講授一個新的數學概念時，不可能不考慮與之有關的舊的數學概念.從學生已有的知識結構體系出發來講授新的數學概念，容易被接受與理解.

比如，在學習除法運算時，學生必須完全了解“什么是平均分”的概念.“平均”在日常生活中是經常會遇到，對此最簡單的理解就是“一樣多”.從這個角度來講除法，學生會容易理解一點.如，7÷3，就是3個3個地分，可以分2次（這個2次就是商的概念），最后還剩下1個（剩下的1個就是余數的概念），所以有7=2×3+1.

又如，多邊形面積的概念，矩形的面積公式最簡單，就是長乘寬，用公式表示就是S=ab.

有些教師在授課時，往往會忽略這些前期的準備工作，忽視了概念之間的前后聯系，而直接步入正題，這樣會在認識上有一個跳躍，對于小學生來說，理解起來就有點費力，無法把知識有機地統一在一起，缺乏一個循序漸進的過程，導致的結果就是背公式.

三、通過數學實踐與活動來加強對概念的理解

“學生掌握數學知識，不能依賴死記硬背，而應以理解為基礎，并在知識的應用中不斷鞏固和深化.”練習題的設計要關注思維訓練的層次，提升思維訓練的難度，“喂飽”學生，提高其思維品質.小學生的圖形想象力與邏輯推理能力都是比較弱，對于一些抽象的數學概念可以讓他們親自做一遍，從而可以獲得切身的體驗.這樣要比看教師演示、聽教師講解更為有效、印象更為深刻.因此，在數學概念的教學上也可以借助數學實踐活動.

如，圓的周長公式為S=2πr，我們一般用字母r表示圓的半徑，那么字母π表示什么意思？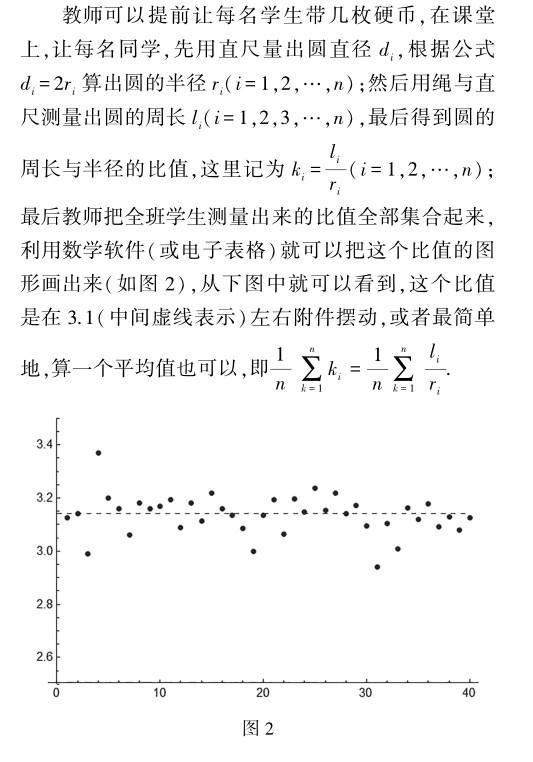

教師可以提示學生，此時的比值應該是一個定值，很可能是無限不循環小數（小學沒有無理數的概念）.這樣就可以得到一個幾何不變量，即所有圓的周長與其半徑之比是一個常數，我們用希臘字母π來表示它，近似值為3.1415926.

教師用這樣的數學活動引入了數學上最重要的常數π.在這個問題上，圓形的種類（即半徑不同）越多，則越能說明問題，給學生的印象就越深.這樣的數學活動給學生一種真實的體驗，這樣的感受不是靠聽教師講解就可以得到地，為引入數學概念做了鋪墊.

四、借助于圖形表示抽象的概念

如果單純地講解概念，學生掌握的知識是孤立的.只有把概念放入相關的知識體系中進行系統化概念教學，學生對概念的理解才更加深刻.

圖形給人的第一印象就是幾何形狀.事實上，數學中的很多概念或問題都可以用圖形來表示，借助于圖形的直觀性，可以簡單明了地表示出問題之間錯綜復雜的關系.通常把概念圖形化之后，就可以大大地降低理解的難度.小學階段經常會遇到單位“1”的問題，不少同學都被這個“1”所困擾.下面就用圖形的方式來表示這個“1”.

如，小紅與小明各有郵票60與40張，小紅給小明多少張之后，可以使得兩人郵票數量之比為1∶4.

五、找關鍵詞、借反例，深刻化概念，提升學生思維的深刻性

比如，在教學“倒數”一課時，學生通過觀察發現這些式子的乘積是1，教師順勢總結倒數的定義———乘積是1的兩個數互為倒數.接下來問學生：你覺得這句話中哪些詞語比較關鍵？學生通過思考認為“乘積是1”在這里最為關鍵，教師接著問學生2-1，1+0，12÷12這些算式的得數也是1，2和1互為倒數嗎？1和0呢？通過觀察，學生發現它們雖然得數為1，但不是乘積是1，只有乘積為1的兩個數才互為倒數.最后讓學生舉幾個互為倒數的例子.這樣通過讓學生找關鍵詞，從正反兩方面舉例的方式進一步加深了對“倒數”含義的理解，提升了學生思維的深刻性.

結 語

總之，在小學數學課堂上概念式教學可以嘗試以下幾種思路，其一就是設法讓學生體會、感受所講的數學概念，正如文中所提到的，可以用數學實踐的方式來感受一下圓周率；其二就是理清概念之間的關系，用已知的概念來發展新的概念，這樣易于學生的理解與接受，最后，可以考慮把抽象的概念圖形化，但是不同的人看問題的出發點通常都不會相同，對同一問題也會有不同的圖形表達，但最終目的只有一個，就是用直觀的方式來展示抽象的概念.上面幾點是筆者在教學過程中總結出來的一點經驗，更多的方式與策略還是需要廣大數學教師努力進行探索.

【參考文獻】

[1]袁冬，小學數學解方程部分存在的問題及對策研究[J].數學教學通訊，2021（1）：63-64.

[2]陸小峰，由《圓的周長》一課，略談“自主探究課型”的幾點思考[J].課程教育研究，2018（5）：134.

[3]楊挺熠，小學分數應用———單位“1”的理解與探究[J].數學學習與研究，2018（13）：119.