加強小學數學開放題教學指導,培養創新思維
李林娟
摘? 要:思維培養的根本目標是鍛煉學生的思維能力,使學生在面對數學問題時可以靈活調用自身的抽象思維、邏輯思維等各種類型的思維來完成問題分析任務,快速找到解題突破口并完成問題求解任務。文章立足小學數學教學現狀,重點對數學開放題教學中思維培養的意義與指導策略進行了探討。
關鍵詞:小學數學;思維能力;開放題;指導策略
一、思維培養的目標
思維培養的根本目標是有效鍛煉及發展學生的思維能力,具體就是指導學生在參與學習活動過程中勤用腦、善思考,有效鍛煉及發展其快速思維能力和反應能力,尤其是要注意指導學生在舉一反三或者其他變式訓練下,結合相關的差異化解題情況,對自己的學習思維進行有效反思,更好地完成相關學習活動中的分析以及其他綜合性學習任務。期間還可以指導學生靈活地應用概括、推理、質疑、反思等一系列思維訓練方式開展思維培訓及訓練。在各項活動開展過程中,要重點鍛煉其思維的新穎性、發散性。在對思維進行培養期間,常用的方法包括設問法、變式訓練、概括推理、創新思維訓練以及一題多解和多變等。在數學學科知識學習或數學問題剖析過程中,隨著學習難度的增加以及抽象概括需求的增加,學生的數學思維從直觀思維向形象思維和邏輯思維發展,是符合學生思維發展邏輯、助力學生解題能力發展的必然選擇。
二、小學數學開放題教學中思維培養的意義
所謂開放題,主要是指那些不具有完備條件和唯一答案的問題,相應地,問題本身呈現多樣化特征,并且解題思路呈現發散性特征,開放題可以在有效促進學生學習數學知識的同時,促進其思維在嚴謹、創新、靈變、發散等方面得到發展,還可以展示其創造性和創新性才華,促進其推理分析能力、閱讀理解能力以及問題求解能力等數學關鍵能力全面發展。開放題本身的題型形式復雜多變,其既可以條件開放,又可以結論開放等,但是無論開放題的“開放”特征處于何地,都要注意滿足學生自思、自探或合作學習等多方面學習需求,力求借助開放題的設計及實施,讓學生在調用自己思維能力求解問題的同時,進一步鍛煉和發展自身思維能力,最終實現思維能力和開放題求解能力的全面發展,避免因為其中某個環節中的解題訓練不到位或者指導不合理而直接影響學生思維能力的最終培養效果,可以抓住開放題設計及實施環節,促進小學生數學核心素養發展。
三、小學數學開放題教學中思維培養的指導策略
(一)巧設條件開放題,開展思維培養
條件是問題求解中需要重點關注的一個核心要素。通過科學設計條件開放題,可以對學生思維的嚴謹與深刻等特性進行有效鍛煉,同時也可以培養學生的觀察能力、問題發現能力和求解能力等綜合能力。因此,在實際的開放題教學中,可以結合現階段小學生的實際經驗等,對問題的條件進行合理增刪,或者借助改變條件的方式來使問題的求解答案不再具有唯一性,還可以在指導學生對相關開放題進行求解的過程中,有效鍛煉其思維能力。但是為了保證條件開放題設計的效果,要注意指導學生重點對其中的有效條件進行挖掘,排除其中不必要的干擾因素,保證基于條件開放題的科學設計,促使學生可以在分析問題的過程中對問題本質進行準確把握,提高其求解數學條件開放題的效率與準確度。
例1:小明家和體育館之間的距離是小冬家和體育館之間距離的4倍,小冬家與體育館之間的距離是600米,他們兩家之間距離是1500米,某一天學校放假后小明從體育館回到家里總計耗時30分鐘,試求小冬家和體育館之間的距離是小明家和體育館之間距離的百分之幾?
解析:本道開放題是一道條件“多余”的問題,是一種比較多見的數學開放題,主要考查的是學生能否對問題求解中的多余干擾因素進行有效排除。在對這類開放題進行求解過程中,教師要注意指導小學生對題干信息認真審查,搞清相關問題的題目求解含義及目標,并要懂得在讀題和審題的過程中,明確其中的關鍵題意,深入挖掘一切可以利用的有價值信息,保證在對多余干擾因素進行有效排除的基礎上,快速確定解題的突破口及思路,最終助力學生快速求解問題。在本道開放題求解過程中,要想求解“小冬家和體育館之間的距離是小明家和體育館之間距離的百分之幾”,首先必須要根據“小明家和體育館之間的距離是小冬家和體育館之間距離的4倍”與“小冬家距離體育館的距離是600米”來相應地推導出小明家和體育館之間的距離,即4×600=2400(米),這時候可得“小冬家和體育館之間的距離是小明家和體育館之間距離的百分之幾”的計算公式為:600÷2400=25%。
通過指導學生認真剖析本道條件開放題,使他們通過認真審題來排除其中影響解題的多余干擾因素和條件,即“他們兩家之間距離是1500米”和“某一天學校放假后小明從體育館回到家里總計耗時30分鐘”。一旦學生在求解本道開放題的過程中準確排除掉這兩個干擾因素,那么最終就可以快速解決問題。由此可見,針對條件開放題的求解,在指導學生求解中要使他們懂得“排干擾”。
(二)巧設問題開放題,開展思維培養
問題開放題主要是開放題目中給出的問題不明確,需要學生在求解問題的過程中,通過自主思考和分析,補充問題求解的相關條件之后再進行求解。在這個過程中,小學生是獨立開展學習活動的個體,他們在解題思路、思維方式以及求解策略等方面存在較大的差異性。基于該種類型問題的分析及求解,可以對學生問題求解的多樣化特征進行剖析,有利于在滿足其個性發展的同時,助力其獨特思維能力得以順利發展。因此,在平時開展開放題教學過程中要注意切實尊重小學生個體本身的差異性,并且要善于指導學生結合數學題目中的有關條件,自主出題及求解問題,充分運用問題開放題的合理設計來調動小學生主體能動性,有效鍛煉及培養其自身的創造性與創新性思維,助力其自身個性得以順利、自由地發展。
例2:小李爺爺在自家果園中栽植了一些蘋果樹與梨樹,已知蘋果樹與梨樹栽植棵數之比為5∶7,______,試求梨樹總計栽植的棵數?
解析:該題是一道經典的問題開放題,在指導小學生求解問題期間,首先要對問題中未給出的問題條件進行補充,再進行求解。問題條件補充的不同,相應的求解思路及方法也會存在一定差異,最終求解問題得到的結果也是各不相同的。通過這種類型的開放題設計及實施,可以有效鍛煉學生的個性化思維和創造性思維,同時也可以借此來促進其創造力的發展。
解:(1)對問題條件進行補充“已知種植的蘋果樹是55棵”,那么此時可知種植的梨樹棵數是:55÷5×7=77(棵),或55÷(5÷7)=77(棵),最終順利求解本道數學題。
(2)對問題條件進行補充“已知種植的蘋果樹比梨樹少18棵”,那么此時可知種植的梨樹棵數是:18÷(7-5)×7=63(棵)。
(3)對問題條件進行補充“已知種植的蘋果樹和梨樹數目總計84棵”,那么此時可知種植的梨樹棵數是:84÷(7+5)×7=49(棵)。
由此可見,在對問題開放題進行求解期間,如果小學生補充的問題求解條件不同,那么就需要采用差異化的求解方法和求解思路,最終得到的求解結果也會有所差異。但是無論學生補充了何種解決問題的條件,最終都可以對他們的個性化思維以及創造性思維等進行有效鍛煉,使其整體思維能力得以有效鍛煉及發展。
(三)巧設結論開放題,開展思維培養
結論開放題主要是給出確定的解題條件,但是沒有給出確定結論的一類數學問題,即數學問題求解過程中涉及的求解思路及方法各不相同,且最終的解題根本目標是促進學生創造性、創新性和個性化思維的全面發展。針對結論開放題的求解,主要是指導小學生結合題干給出的解題信息,從多維度進行思考,保證最終獲得合理、準確的解題結果。
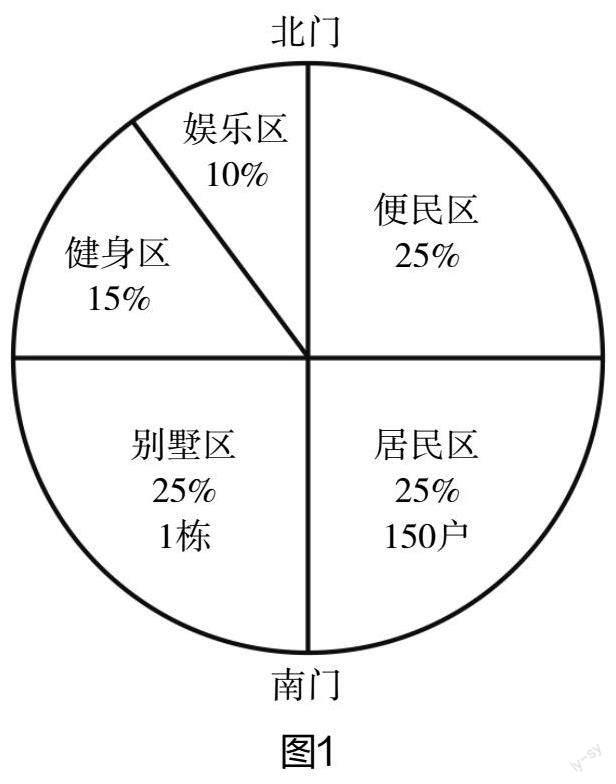
例3:如圖1是某一個住宅小區的構成圖,南門和北門之間直線距離為160m,并且劃分成了眾多功能分區,試求:①本小區總計占地面積為多少?②小明每天在小區外側會進行慢跑,每天跑5圈,試求小明每天會慢跑多長距離?③住宅小區物業公司為了響應“垃圾不落地,構建魅力社區”的號召,在小區內部推行了“垃圾分類”活動,現在想要在小區中建造一個“社區環保屋”,那么你覺得應該修建在小區的哪個位置呢?試用△進行標注,并說一說自己的理由?
解析:針對本道結論開放題的求解,學生根據題干信息可以快速意識到本道題實際上就是“圓的周長和面積”方面的知識的應用。針對問題①和問題②的求解,學生只需要結合題干給出的南北門直線距離是160m來確定這個圓的半徑是80m,之后可以直接代入圓的面積和周長計算公式來進行快速計算。而針對本道結論開放題的問題③,學生在進行求解的過程中需要綜合考慮多方面的因素,如各功能區域的人數以及垃圾雜物產生量,垃圾投遞便捷性和安全性等,所以本道題的正確答案可能并不是唯一確定的,只要是學生結合自己的學習情況給出了自己的看法,那么就應該及時進行鼓勵和表揚,切不可利用“一刀切”的答案設計方式影響部分小學生學習的積極性,否則也會直接限制其個性發展和創新性思維能力發展。
(四)巧設綜合開放題,開展思維培養
除上述幾種類型的開放題外,綜合開放題也是比較多見的開放題,主要是對給定數學問題中的條件、方法、結論等進行調整來設置綜合性開放問題,借此來對小學生綜合運用數學知識的能力進行考查。在對該種類型的數學開放題進行設計的過程中,主要的設計出發點是突出及強化“綜合”這一特征,即引導全體小學生多方位、多角度開展深入思考活動,并在指導他們對問題進行分析及求解的過程中來鍛煉其自身的思維能力。
例4:在放寒假前,小紅和她的一些小伙伴打算出去游玩幾天,現在已經獲得了她們家長的同意,并且給了她們1500元旅游費用,但是規定時間不能超過3天,回到家的時間也不能夠超過晚上7點,試幫助她們設計一份最佳的旅游出行計劃。
解析:本道開放題的設計初衷是對學生的綜合能力進行有效鍛煉,但是為了保證最終順利設計出一份絕佳的出游計劃,可以指導學生親自動手查詢自出發點到旅游點的輪船、公交車等多種交通工具的票價及時刻表等,明確相關旅游景點的門票價格以及其他關鍵的旅游信息,將這些知識與學生的生活實際進行有機結合,借助這種開放題設計方式可以在鞏固學生所學數學知識的同時,對他們的思維進行激活,不僅可以促進其創造性思維的發展,還可以全面鍛煉及發展其信息搜集、剖析、歸納及篩選等能力。因為在求解本道綜合開放題過程中,不僅需要學生調用以往數學學習過程中的相關知識內容,還需要有計劃地應用自身的數學知識綜合運用能力。比如有的學生會在選擇自己感興趣的旅游景點基礎上,繼續有序地對相關的出行時間進行考慮,借助這種有序分析的思維運用方式,可以很好地鍛煉學生的邏輯思維、創造性思維以及其他一些高階思維能力,最終可以全面促進其自身數學綜合素質發展,助力其數學核心素養的順利養成。
總之,思維培養是新課程理念下培養學生數學核心素養的一個根本要務,會對學生數學綜合素質發展產生極大影響。而開放題設計及實施是鍛煉學生思維能力發展的一個重要路徑,所以在實際的數學開放題設計中可以結合學生的思維培養目標,靈活地設計條件開放題、問題開放題、結論開放題以及綜合開放題等不同類型的開放題,借助開放題的有效設計及教學指導助力學生思維能力得以發展。
參考文獻:
[1]楊寧,滿長江. 淺析構建小學數學開放式課堂的策略研究[J]. 科幻畫報,2021(09):79-80.
[2]陶玲俐. 小學數學開放式教學法的應用策略[J]. 試題與研究,2021(23):17-18.
[3]郝海平. 小學數學開放題研究再思考[J]. 新課程研究,2019,515(15):12-13.
(責任編輯:鄒宇銘)

