素養立意穩中有變考教銜接助力改革

【摘 要】 ?2023年高考數學新課標Ⅰ卷嚴格依據高中數學課程標準，深化基礎性和綜合性考查，在試題變化上把握充分，在素養立意上體現充分，在考教銜接上助力充分，精選試題情境，助力高中育人方式改革.

【關鍵詞】 ?新課標Ⅰ卷;試題變化;素養立意;考教銜接

2023年是八省市全面使用新教材后的新高考元年.2023年高考數學新課標Ⅰ卷（以下簡稱“Ⅰ卷”）表達簡約，給人一種“春風拂面”的舒適感和一種“似曾相識”的熟悉感.數學語言表達精煉，閱讀理解上通俗易懂；試題立意與設問十分“友好”；每道題入手容易，且都能拿到與自己水平相當的分數，給學生一種明顯的“獲得感”.通過比較研究2021年、2022年新課標Ⅰ卷可以發現，2023年Ⅰ卷這種“簡約”“友好”和“獲得感”，主要歸因于本文接下來要論述的“三個充分”.

1 ??試題變化把握充分

每年的高考試題設問或考點分布都有“變”與“不變”的部分.總結今年的Ⅰ卷，“不變”的部分往往讓考生能潛意識地接受，比如第1題考查的“集合的交集”，第2題考查的“復數的運算”；基礎解答題中依然是考查“解三角形”，放在17題位置；第18題的立體幾何是傳統的數學情境，以正四棱柱為載體，第一問考查常規的“線線平行”，第二問還是考查二面角余弦等等.而“變”的部分，能反應高考試題的變化趨勢，具體體現如下： 1.1 必備知識的分布調整

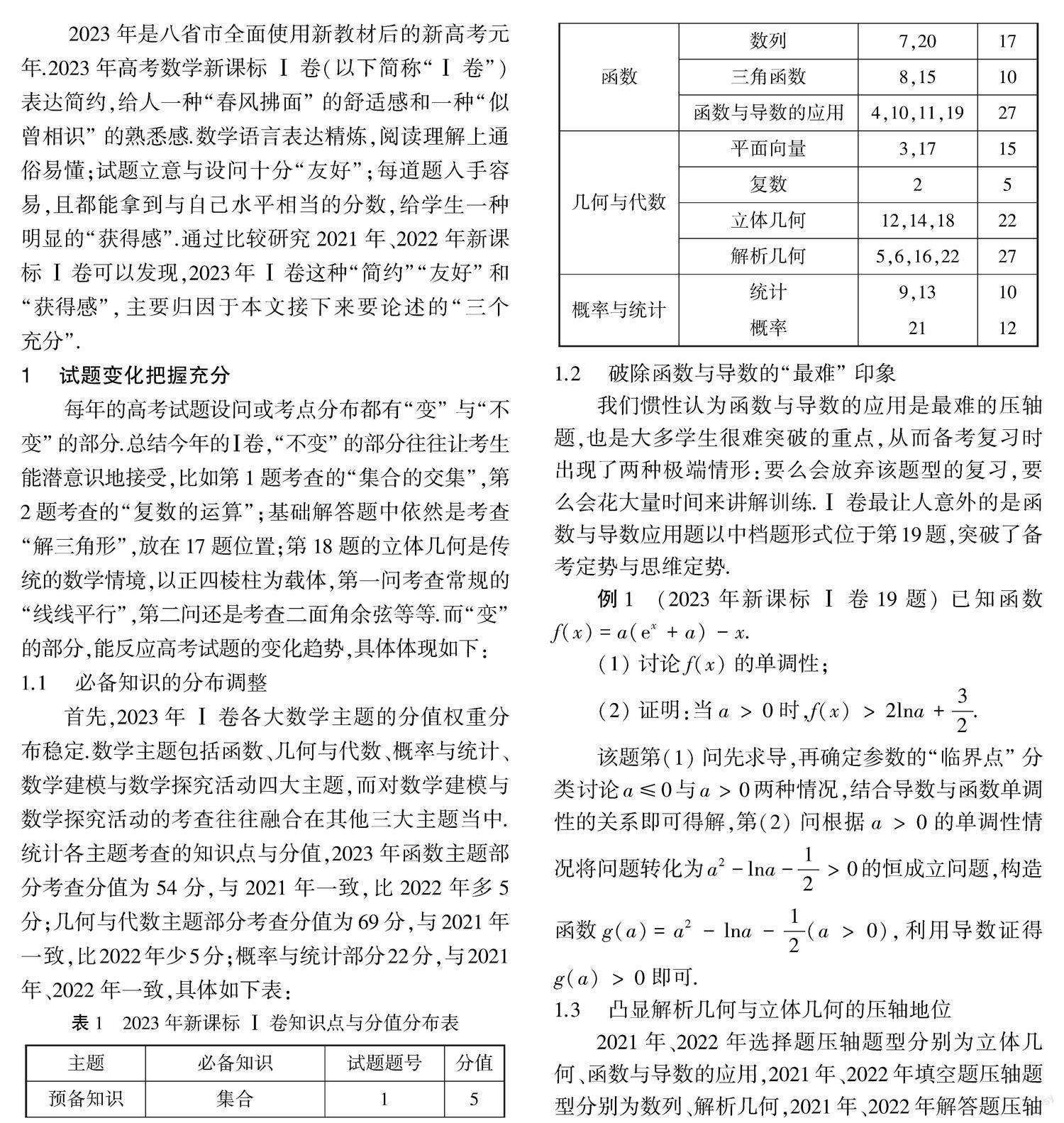
首先，2023年Ⅰ卷各大數學主題的分值權重分布穩定.數學主題包括函數、幾何與代數、概率與統計、數學建模與數學探究活動四大主題，而對數學建模與數學探究活動的考查往往融合在其他三大主題當中.統計各主題考查的知識點與分值，2023年函數主題部分考查分值為54分，與2021年一致，比2022年多5分；幾何與代數主題部分考查分值為69分，與2021年一致，比2022年少5分；概率與統計部分22分，與2021年、2022年一致，具體如下表：

1.2 破除函數與導數的“最難”印象

我們慣性認為函數與導數的應用是最難的壓軸題，也是大多學生很難突破的重點，從而備考復習時出現了兩種極端情形：要么會放棄該題型的復習，要么會花大量時間來講解訓練.Ⅰ卷最讓人意外的是函數與導數應用題以中檔題形式位于第19題，突破了備考定勢與思維定勢.

例1 ?（2023年新課標Ⅰ卷19題） 已知函數f（x）=a（ex+a）－x．

（1）討論f（x）的單調性；

（2）證明：當a>0時，f（x）>2lna+ 3 2 ．

該題第（1）問先求導，再確定參數的“臨界點”分類討論a≤0與a>0兩種情況，結合導數與函數單調性的關系即可得解，第（2）問根據a>0的單調性情況將問題轉化為a2－lna－ 1 2 >0的恒成立問題，構造函數g（a）=a2－lna－ 1 2 （a>0），利用導數證得g（a）>0即可.

1.3 凸顯解析幾何與立體幾何的壓軸地位

2021年、2022年選擇題壓軸題型分別為立體幾何、函數與導數的應用，2021年、2022年填空題壓軸題型分別為數列、解析幾何，2021年、2022年解答題壓軸題型均為函數與導數的應用，然而2023年Ⅰ卷的選擇題、填空題、解答題的壓軸都以“幾何壓軸”的形式出現，規避了猜題、押題的“投機”行為.

例2 ?（2023年新課標Ⅰ卷12題）下列物體中，能夠被整體放入棱長為1（單位：m）的正方體容器（容器壁厚度忽略不計）內的有

A.直徑為0.99 m的球體

B.所有棱長均為1.4 m的四面體

C.底面直徑為0.01 m，高為1.8 m的圓柱體

D.底面直徑為1.2 m，高為0.01 m的圓柱體

該題設計以數量關系來刻畫位置關系.在正方體內放入其他幾何體，需要考慮正方體的面對角線、體對角線.A，B，C選項很容易從數量上進行判斷，而D選項中正方體內嵌入底面直徑或高超過棱長的圓柱體，要將圓柱體擺放為與體對角線垂直的狀態，需要很強的空間想象能力并進行精妙的數據運算.

例3 ?（2023年新課標Ⅰ卷16題）已知雙曲線C： x2 a2 － y2 b2 =1（a>0，b>0）的左、右焦點分別為F1，F2．點A在C上，點B在y軸上，F1A ⊥F1B ，F2A =－ 2 3 F2B ，則C的離心率為 ????．

該題可以利用雙曲線的定義與向量數積的幾何意義得到 AF1 ， AF2 ， BF1 ， BF2 關于m，a的表達式，根據垂直的條件得到m=a，接著利用余弦定理得到a，c的齊次方程；也可以設出點A，B的坐標，根據坐標法及坐標運算，得到點A，B的坐標關系，再根據A點在雙曲線上，可得到關于a，b，c的齊次方程.

例4 ?（2023年新課標Ⅰ卷22題）在直角坐標系xOy中，點P到x軸的距離等于點P到點 0， 1 2 ?的距離，記動點P的軌跡為W．

（1）求W的軌跡方程；

（2）已知矩形ABCD有三個頂點在W上，證明：矩形ABCD的周長大于3 3 ．

本題中拋物線方程不是標準方程，而是頂點不在原點的二次函數的結構形式，同時最值求解的式子是關于兩個參數的含雙絕對值的結構式 1+k2 ??2m－k + 1 k ?2m+ 1 k ??，需要考慮函數f（m）=|2m－k|+ 1 k |2m+ 1 k |（0 k 2 ???進行分段討論．

1.4 鞏固概率與統計的“新主角”地位

概率統計專題的復習無固定“套路”可循.2021年位于18題位置，以“一帶一路”知識競賽為情境設置“求累計得分的分布列”“根據期望值做決策選擇答題順序”的問題形式；2022年位于20題位置，以“研究疾病與衛生習慣關系”為情境設置“獨立性檢驗”“證明條件概率等式”“根據樣本數據估值”等問題形式.2023年Ⅰ卷將概率統計與等比數列遞推公式融合在一起考查，載體與試題位置都類似于2019年全國Ⅰ卷理科第21題，屬于偏難題型，可以說直接承擔了“人才選拔”的功能，也表明了概率與統計情境與形式上的創新，逐漸成為了高考數學的“新主角”.

例5 ?（2023年新課標Ⅰ卷21題）甲乙兩人投籃，每次由其中一人投籃，規則如下：若命中則此人繼續投籃，若未命中則換為對方投籃．無論之前投籃情況如何，甲每次投籃的命中率均為0.6，乙每次投籃的命中率均為0.8，由抽簽確定第1次投籃的人選，第一次投籃的人是甲、乙的概率各為0.5．

（1）求第2次投籃的人是乙的概率；

（2）求第i次投籃的人是甲的概率；

（3）已知：若隨機變量Xi服從兩點分布，且P（Xi=1）=1－P（Xi=0）=q1，i=1，2，…，n，則E ∑ n i=1 Xi =∑ n i=1 qi．記前n次（即從第1次到第n次投籃）中甲投籃次數為Y，求E（Y）．

該題首先需要思考第（1）問和第（2）問的關系，為什么第（1）問是“求第2次投籃的人是乙的概率”，而第（2）問卻是“求第i次投籃的人是甲的概率”？比如i=2時甲、乙投籃概率關系，從而需要建立“第i次投籃是甲的概率是pi，則第i次投籃的人是乙的概率是1－pi”的邏輯關系，再根據遞推關系，構造等比數列模型；其次需要思考前一次甲、乙投籃都對后一次投籃產生影響；最后需要理解兩點分布的數學期望與甲投籃次數的數學期望滿足等式關系.

第（2）問解析：設pi表示第i次投籃是甲的概率，則第i+1次投籃是甲的概率pi+1= 3 5 pi+ 1 5 （1－pi），即pi+1= 2 5 pi+ 1 5 ．

構造{pi+λ}為公比為 2 5 的等比數列，有pi+1+λ= 2 5 （pi+λ），解得λ=－ 1 3 ．由p1－ 1 3 = 1 6 ，可得：當i≥2時，則pi－ 1 3 = 1 6 ??2 5 ?i－1，即pi= 1 3 + 1 6 ??2 5 ?i－1．又p1= 1 2 也滿足該式，故pi= 1 3 + 1 6 ??2 5 ?i－1．

第（3）問解析：設第i次投籃人是甲時，Xi=1；第i次投籃人是乙時，Xi=0，則Xi服從兩點分布，有P（Xi=1）=pi．從而

E（Y）=E（∑ n i=1 Xi）=∑ n i=1 pi=∑ n i=1 ??1 3 + 1 6 ??2 5 ?i－1 = 1 3 n+ 1 6 ∑ n i=1 ??2 5 ?i－1= 1 3 n+ 5 18 － 5 18 ??2 5 ?n．

1.5 強化數列的“計算”立意

近兩年以來，數列綜合應用的計算要求越來越高，比如2021年考查“剪紙藝術中對折紙的種類及表面積問題”“遞推關系求通項求和問題”，2022年考查“消和式并累乘求通項問題與裂項相消求和后證明不等式問題”.同樣，2023年Ⅰ卷對等差數列的相關計算也提出了相當高的要求，并且計算過程反套路.

例6 ?（2023年新課標Ⅰ卷第20題）設等差數列{an}的公差為d，且d>1．令bn= n2+n an ，記Sn，Tn分別為數列{an}，{bn}的前n項和．

（1）若3a2=3a1+a3，S3+T3=21，求{an}的通項公式；

（2）若{bn}為等差數列，且S99－T99=99，求d．

該題命題意圖是研究兩個等差數列乘積，第（1）問需要在“S3+T3=21”的條件下通過例舉b1，b2，b3計算得到a1，a2，a3之間的關系，從而求得d；第（2）問借助{bn}為等差數列通過2b2=b1+b3計算得到a1與d的關系，再通過條件S99－T99=99分情況討論計算得出結果．

2 ??素養立意體現充分

高考命題體現的是“價值引領、素養立意、能力為重、知識為基”的變化趨勢，而“素養立意”在2023年Ⅰ卷中的體現是：在“重點考查邏輯推理素養、深化考查直觀想象素養、扎實考查數學運算素養”[1]基礎上，還兼顧了充分考查數學抽象素養、簡化考查數學建模素養.2.1 充分考查數學抽象素養

例7 ?（2023年新課標Ⅰ卷第11題）已知函數f（x）的定義域為 R ，f（xy）=y2f（x）+x2f（y），則

A．f（0）=0 ?B．f（1）=0

C．f（x）是偶函數

D．x=0為f（x）的極小值點

該題考查抽象函數的性質，A，B，C可通過賦值得出，而D選項需要根據前面三個選項，通過抽象到具體構造特殊函數

f（x）= x2ln|x|，x≠0，0，x=0.

2.2 簡化考查數學建模素養

模型是“數學的語言”，是描述世界的工具.模型在高考數學中包括了函數模型、幾何模型、不等式模型、概率模型等.2023年Ⅰ卷中選取科學情境“噪聲污染問題”，簡化地考查了函數模型選擇與應用過程.

例8 ?（2023年新課標Ⅰ卷第10題）噪聲污染問題越來越受到重視．用聲壓級來度量聲音的強弱，定義聲壓級Lp=20×lg p p0 ，其中參數p0（p0>0）是聽覺下限閾值，p是實際聲壓．下表為不同生源的聲壓級：

已知在距離燃油汽車、混合動力汽車、電動汽車10 m處測得實際聲壓分別為p1，p2，p3，則

A．p1≥p2 ????B．p2>10p3C．p3=100p0 D．p1≤100p2

該題聯系實際，注重應用，利用對數函數研究噪聲聲壓水平，通過對聲壓級的研究，可以直接用原函數模型Lp=20×lg p p0 處理，也可以轉化為實際聲壓函數p=p0×10 Lp 20 處理，體現了模型選擇和應用過程. 3 ??考教銜接助力充分

高考的核心功能之一就是“引導教學”，高考數學試題中呈現“考教銜接”的導向就是對“雙減”政策最好的呼應.教育部教育考試院在“高考命題實現由‘以綱定考到‘考教銜接的轉變中”指出，高考命題要嚴格依據高中課程標準，確保“內容不超范圍，深度不超要求”，考查內容限定在課程標準范圍之內，考查難度限定在技能能力要求之內.2023年Ⅰ卷，很好地從這兩個方面作了呈現.3.1 深度充分銜接課標 例9 ?（2023年新課標Ⅰ卷第9題）有一組樣本數據x1，x2，…，x6，其中x1是最小值，x6是最大值，則

A．x2，x3，x4，x5的平均數等于x1，x2，…，x6的平均數

B．x2，x3，x4，x5的中位數等于x1，x2，…，x6的中位數

C．x2，x3，x4，x5的標準差不小于x1，x2，…，x6的標準差

D．x2，x3，x4，x5的極差不大于x1，x2，…，x6的極差

該題考查了統計抽樣中樣本的基本數字特征，考查考生對樣本的平均數、標準差、中位數、極差概念的理解和掌握，難度要求符合課標要求，對接如下：

用樣本估計總體 能用樣本估計總體的集中趨勢參數（平均數、中位數、眾數）；能用樣本估計總體的離散程度參數（標準差、方差、極差） 結合具體實例，理解

3.2 內容充分回歸教材

“源于教材，但不拘泥于教材”是新高考的命題特點，那么可以從高考試題的顯性要素與隱性要素兩方面去建立與教材的對接點[2].比如，Ⅰ卷第3題含參數的向量的垂直關系，來源于必修二第60頁復習題參考題第6題；第10題噪聲污染問題來源于數學必修第一冊第141頁習題4.4中第10題“聲強”問題，具體內容為：

教材對接 ?聲強級L1（單位：dB）由公式L1=10lg ?I 10－12 ?給出，其中I為聲強（單位：W/m2）.

（1）一般正常人聽覺能忍受的最高聲強為1W/m2，能聽到的最低聲強為10－12W/m2.求人聽覺的聲強級范圍.

（2）平時常人交談時的聲強約為10－6W/m2，求其聲強級.

鑒于此，2023年Ⅰ卷選擇題部分與教材的顯性鏈接可初步統計如下：

4 ??考教銜接背景下的備考策略

總的來說，2023年Ⅰ卷嚴格依據高中數學課程標準，深化基礎性和綜合性考查，聚焦學科核心素養，體現“考教銜接”導向.“考”與“教”的銜接，并不是簡單的“以考定教”或者是“以教定考”，而是一定要明確“銜接什么”“怎么銜接”“銜接后如何教學”的問題.因此，高考與教學的銜接就需要研究“銜接”的標準是什么，相關的“銜接”機制如何建立.

4.1 歸納考點，對標課標

要及時準確歸納每年高考考點，從“四翼”（怎么考）的角度，對標課標內容范圍與能力要求，這樣教學才能實現“高考導向”，才能實現“引導中學依標教學”的目標.

4.2 梳理教材，整合教材

復習備考中要思考如何通過對高考題和教材習題的比較、研究，建立高考試題與教材的對接點. 比如靈活運用顯性關聯和隱性關聯兩種方式，梳理試題材料呼應教材的出處，梳理題干設問、答案設計與教材中的重點內容建立知識鏈接等.同時，在梳理教材的基礎上，挖掘教材資源，進行考點專題分類，提煉數學思想與通性通法，增強和教材的關聯度.

4.3 轉變方式，單元教學

因為教師往往對考試內容變化敏感，即“考了什么沒考什么”“哪個主題考的多，哪個主題考的少”如數家珍，并且能夠積極主動調整復習方向，但教學方法的調整卻受諸多因素的影響而“一成不變”.所以高考數學內容的變化對教學內容范圍的影響迅速而深刻，但對教學方式方法的影響十分不明顯，很多高三的復習課堂現實情況往往是“不管你怎么考，我就是這樣教”.因此，在新課程、新課標、新教材和新高考的背景下，要順應高考命題“價值引領、素養立意、能力為重、知識為基”的變化趨勢，就必須變革課堂教學方式，實現真正意義上的由“解題”到“解決問題”的轉變；要實行大概念單元教學，落實必備知識，通過“情境創設—問題設計—探究活動”的教學過程，精心設計問題鏈，強調在深刻理解基礎之上的融會貫通、靈活運用，讓學生掌握原理、內化方法、舉一反三，引導學生主動探究，達到實現深度學習的目的.

參考文獻

［1］ ?教育部教育考試院.2023年高考數學全國卷試題評析[EB/OL]. （2023-06-07）[2023-06-08].https：//mp.weixin.qq.com/s/7SgNZ_RKg7V4FGJvbh_w9g.

［2］ ?周威.高考導向下的數學復習教材回歸策略淺談[J].數學通訊，2020（20）：43-45.

作者簡介 ?周威（1985—），男，中學一級教師，基礎數學碩士；湖北省恩施州教育科學研究院高中數學教研員，恩施州高中數學教學指導委員會秘書;研究方向為教育評估與高中數學教育；發表論文80余篇.