把握數學度量本質　促進結構化教學

摘要：在核心素養導向下，小學數學結構化教學要精準把握教學內容之間的關聯，夯實教學內容主線，發展與之相關的學生核心素養。多邊形面積的計算具有很強的抽象性，教師要把握度量本質，引導學生感悟學科知識本質一致性，進行知識結構化、學習過程結構化、思維結構化的教學，發展學生的結構化思維。

關鍵詞：核心素養；度量本質；結構化教學

《義務教育數學課程標準（2022年版）》（以下通稱“新課標”）指出，在教學中要重視對教學內容的整體分析，幫助學生建立能體現數學學科本質、對未來學習有支撐意義的結構化的數學知識體系。結構化教學要求教師站在整體的視角，運用聯系的觀點對教學對象、學習過程、學生思維進行全面、系統得把握。教師在教學中要形成一個“從宏觀到微觀”的總體框架，“望”知識的過去、現在和未來，對知識進行結構化；“望”學生動態的學習過程，選擇合適的學習策略，對學習過程進行結構化；“望”學生數學思維的發展，高位引導，對數學思維進行結構化。

一、縱向把握度量本質，促進數學知識結構化

面積單位度量教學北師大版數學教材安排在三個不同學年，在二年級上冊安排長度的測量，也就是一維圖形的度量，本質是長度單位的累加，可以看成是幾個長度單位=長度；在五年級上冊安排面積的測量，也就是二維圖形的度量，本質是面積單位的累加，可以看成“一行里單位面積的個數×行數=面積”；在五年級下冊安排立體圖形體積的測量，也就是三維圖形的度量，本質是體積單位的累加，可以看成“一行里單位體積的個數×行數×層數=體積”。平行四邊形面積的計算是二維圖形度量的一部分，距離學生學習長方形和正方形面積的計算已經有兩年時間，學生對面積度量本質有所遺忘，而平行四邊形面積的計算公式的推導又比較抽象，學生要尋得本質進行學習難度較大。教師應立足于面積度量本質進行教學設計，應注重本節課承上啟下的作用。在復習過程中，教師應引導學生感受知識的根源與螺旋上升特點，將知識系統化、結構化。

【教學片段1】

1.出示一條線段：你知道這條線段的長度嗎？

生：用尺子量一量線段中有幾個1厘米，就是幾厘米。

2.出示標有長和寬的長方形：你會算這個圖形的面積嗎，你是怎么得到這個長方形的面積的？

生：我是用“長×寬”計算出來的。

生：一行有6個1平方分米，4行有24個1平方分米，就是24平方分米。

【設計意圖】復習線段的度量和長方形面積的度量，喚醒學生已有的系統知識，為本節課知識的學習做好準備；復習長方形面積計算公式及其度量本質，為平行四邊形面積計算推導做好準備。

3.出示練習：瞧，發生了什么事？

巴依老爺正在賣草皮苗（見圖1）：“每平方米草皮10元。以下草皮都是用24米繩子圍成的，價格都是一樣的。”阿凡提趕緊阻止說：“等一等，等一等，不要著急著買！”你們知道阿凡提為什么要阻止嗎？（雖然都是用24米繩子圍成的，但是面積不一樣）

【設計意圖】將知識與現實世界進行關聯，遵循學生的年齡特征設置情境，當長方形和平行四邊形的面積的對比涉及個人智慧的體現時，學生會以最快的速度調動已有經驗解決問題，感受知識對解決真實問題的幫助，激發學習的欲望，化被動學習為主動學習。數據的設計呈現出周長相同，底不變，學生在具體的情境中感受高的不同所帶來的面積的變化，將注意力集中到決定面積大小的“高”上，也初步感知平行四邊形面積與斜邊長短沒有關系，促進數學思維的發展。

二、整體把握課程組織，促進數學學習過程結構化

學生的學習是一個動態的過程，在學習過程中形成特定的思考方法、學習策略、探究過程等，就是一種學習過程結構化。通過學習過程結構化，教師可以引導學生在學習過程中進行學習方法的有效遷移，提高學生的數學學習能力。

本節課設計，從情境創設中引導學生“發現問題”：同周長面積不一定相等，那么面積的大小和什么因素有關呢？學生根據已有的知識經驗進行大膽猜測，教師設置探究過程，引導學生“驗證猜測”以解決問題，最后通過變式練習，引導學生應用知識。這一結構化的學習過程，可以很好地應用到對三角形、梯形面積計算的推導中，甚至應用到相關課型的知識學習上。學生的探究力就在學習過程結構化中得到不斷夯實和提升，進一步提高學習能力。

【教學片段2】

猜想驗證，探索本質：這些圖形的面積一樣大嗎？（不一樣大）這些是同學們的猜測，你能用你的方法揭開巴依老爺的陰謀嗎？

探究活動：

1.誰的面積大？

2.要求獨立思考后，用自己喜歡的方式，驗證自己的想法（教師提供平行四邊形、格子圖、剪刀）。驗證完成后，在小組內交流自己的方案。

生：我用數格子的方法，將合起來能組成一個完整格的小格子進行組合，再數完整格有幾格（見圖2），加起來是28格，1格代表1平方米，因此是28平方米。

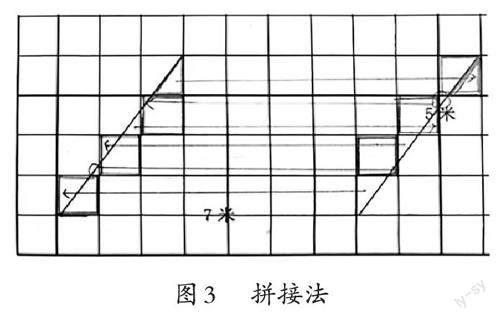
生：我把不完整的一小格剪下來拼到另一邊，發現剛好拼成一個正方形，剩下的不完整的格子也是一樣，就湊成了完整的格子（見圖3）。這樣就有4行，每行有7格，7×4=28格，是28平方米。

生：我直接把左邊這個三角形剪下來，平移到右邊，我發現所有的格子也都是一整格的了，而且我還發現，圖形變成了長方形（見圖4）。這樣就很好求面積了，用長×寬=長方形面積，也就是4×7=28平方米。

師：同學們經過動腦思考，得出了這么多的解題方案。在數的過程中，你們有沒有發現什么不變？什么變了？（引導學生感受割補法這種化零為整的轉化方法）

生：形狀變了，面積不變。

師：最后這種方法，用到了長×寬，為什么不用長×斜邊呢？

生：這里剪拼后是一行有7格，一共有4行，并不是5行，不能乘5，否則就沒有意義了。

【設計意圖】圖2為帶格子的平行四邊形，教師可以讓學生嘗試用數格子的方法解決問題，題中并沒有交代“不滿一格算半格”的規則，能有效規避學生對這種規則的排斥。由于有部分學生也會運用平移的方法，所以在本環節中教師主要是讓學生放開思維、充分說理，引導學生發現平移的方法是為了數“完整的格子”，比直接數格子更科學、直觀；在操作過程中，學生運用轉化的數學思想方法將未知轉化成已知，辨析與平行四邊形面積大小有關的因素，最終推理出其計算公式。

三、橫向把握面積度量本質，促進數學思維結構化

結構化思維指的是能夠從多角度對數學問題展開觀察、分析，并利用關聯性、系統性、整體性的思維找到解題策略，找到解決數學問題的思維方法。

在本節課的教學中，教師可以依托面積度量本質，引導學生橫向對比分析不同圖形的特征，遷移面積計算推理學習方法，也可以從圖形維度角度入手，引導學生發現、總結一維和二維圖形面積的度量本質，從而聯想到三維圖形的度量。通過這樣的引導，學生形成結構化的數學思想以及結構化的問題解決策略和方法，也就是形成一種更為上位的結構化思維。

【教學片段3】

師：通過本節課的學習，你覺得你可以解決三角形、梯形的面積計算問題嗎？

生：三角形和梯形里也含有不完整的面積單位，與平行四邊形面積計算方法相同，先進行切割，轉化成長方形或者平行四邊形，就可以求出它們的面積了。

【設計意圖】方法遷移，感受知識的統一性：轉化成底為多少、高為多少，就可以計算有幾個這樣的面積單位。

師：我們已經學習了一維圖形的測量，需要用到長度單位進行累加，又學習了二維圖形的測量，將不完整的面積單位轉化成完整的面積單位進行累加，那么，同學們還想學習什么知識呢？

生：三維圖形的測量，比如長方體的大小測量。

師：你能猜猜如何測量長方體的大小嗎？

生：它應該也像長度和面積一樣有厘米和平方厘米這樣的度量單位，然后看里面有幾個這樣的度量單位。

【設計意圖】在學習完平行四邊形面積后，教師引導學生思考，如果以后遇到不同的二維圖形應該如何度量，讓學生知道求面積就是算有幾個這樣的面積單位，運用轉化的數學思想，將未知轉化成已知，進行知識的遷移；再引導學生從一維到二維再到三維圖形的度量上思考，感受度量本質知識的一致性，建立起結構化思維。

在教學過程中，教師要重視對教學內容的整體分析，厘清知識體系、對標學習過程策略，引導學生在學習過程中形成結構化思維，讓學生能夠自信地成為學習主體，有方法、有策略地發現問題，并積極思考探究、解決問題，進而發展學生的核心素養。

參考文獻：

［1］王良燕.讓兒童經歷數學概念學習的全過程［J］.基礎教育研究，2016（22）.

［2］陶壽山.質疑：探究教學模式在烹飪教學中的有效運用［J］.當代教育實踐與教學研究，2017（11）.

（責任編輯：楊強）

作者簡介：陳輝玲，福建省廈門市集美區實驗小學一級教師。