作圖使數學問題開出別致的花

陳梅

摘要：解決問題是數學教學的重要內容。在教學中，要讓學生主動從數學的角度運用所學的知識和方法尋求解決問題的策略。畫圖策略是解題策略中最基本的，也是一個非常重要的策略。它能幫助學生把抽象的文字問題直觀化、具體化，使學生能更好地理解題意，正確地找出其數量關系，確定解題方法。本文對教學中學生運用畫圖策略來解答問題存在的一些問題進行分析，發現從激發興趣，體驗畫圖樂趣，教會方法，體現畫圖價值這兩方面進行畫圖策略的訓練，可提高低年級學生解決問題的能力，拓展他們的數學思維。

關鍵詞：小學數學? 畫圖? 問題解決? 研究

“老師，看到這個點子圖我一下子就明白了，怎樣寫乘法算式。”這就是我上完二年級上冊《有多少個點子》這一課，學生們高興地對我說。一節數學課在學生們快樂地畫圖中上完了。作為一名數學教師我們該如何使學生在解決問題中能正確地運用畫圖來解答數學問題呢？我主要從以下幾方面進行了嘗試。

一、激發興趣，體驗畫圖樂趣

低年級學生現正處于以形象思維為主，逐漸過渡到抽象思維。但現在許多數學問題卻都以文字形式出現，學生們常常讀不懂題意，導致不知道如何解答問題。根據這一年齡特點，教師可以讓學生們平時多畫一畫、涂一涂，借助實物圖或線段圖等把抽象的數學問題具體化。這樣能使他們更好地理解題意，同時也能幫助他們找到解決問題的關鍵，提高他們解決問題的能力。因此，教師在教學中要善于創設體驗情境，讓學生在思考的過程中培養畫圖意識，樂于畫圖，并在畫圖的過程中加深對所學知識的理解，發展自身的數學思維。

（一）感受畫圖策略的重要性

教師要及時指導學生用畫圖的策略來解決問題，讓他們體會到畫圖的重要。如，小朋友們排隊做操，從左邊數起笑笑排在第6個，從右邊數起笑笑排在第8個，一共有多少個小朋友？

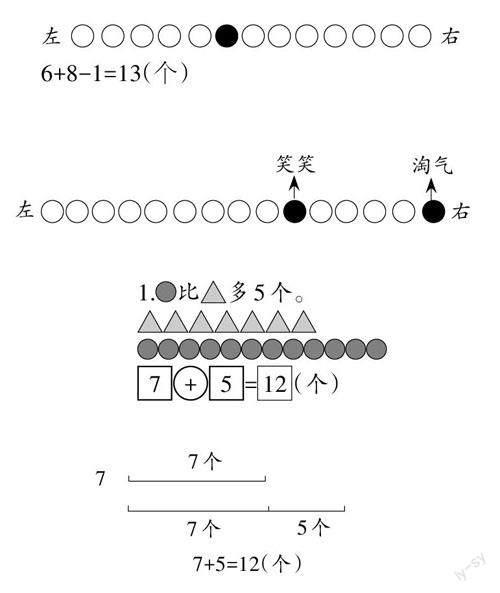
這題對于一年級學生來說的確有點難，這時可以指導學生們一起跟教師畫畫圖，如下圖：

6+8-1=13（個）

這樣一畫圖就容易理解這個算式的意思，能直觀地看出笑笑多數了一次，其實笑笑左邊只有5個人，右邊只有7個人，再加上笑笑一共只有13個人，多數的一次要把它減掉，所以算式就是： 6+8-1=13 （人）。

學生們看圖后會發現：原來這么簡單啊！從中讓他們意識到原來很多題目可以通過畫圖來解決，而且一畫圖題目就變簡單了，這樣讓他們對畫圖的興趣會越來越濃。

（二）重圖意的表達，輕美觀

在教學中，若學生用畫圖策略來解答時，畫得不是很規范、美觀時，教師都要及時給予表揚。這樣下去，學生們畫圖的興趣會越來越高，而且也會畫得越來越標準、美觀，解決問題的能力也在不斷提高。例如，二年級下冊有如下試題： 一袋糖有60顆，已經吃掉24顆，剩下的糖平均分給6個小組，平均每個小組能夠分到幾顆？

有些學生畫的線條彎彎扭扭的，畫得不是很美觀，但他們知道怎么去畫圖。讓他們慢慢地多畫，一定能畫標準、畫美觀的。且學生受到過表揚后，畫圖的積極性會更高。

在教學中慢慢地讓學生用畫圖的策略來解決問題。數形結合，以畫促思，把復雜問題簡單化，化抽象為直觀，從而更好地解答問題。同時，也讓學生體會到畫圖解題的樂趣，體驗到畫圖法解題所帶來的成功感。

二、教會方法，體現畫圖價值

所謂的畫圖策略就是把問題呈現的信息通過圖畫的形式表示出來，并從中尋找解決問題的策略。同時在教學中教師要教會學生們解題的方法，而要讓學生們用畫圖策略來解決問題，首先要教會他們如何來畫圖。

（一）實物圖過渡到示意圖

在解決問題的過程中，很多學生會根據自己的經驗，會畫出一些自己喜歡的圖來解決問題。

例如：一年級上冊“小朋友們排隊，笑笑排在第10個，淘氣排在第15個，笑笑與淘氣之間有多少人？”

在解決這道題時，學生們采用了不同的畫圖策略，發現有些學生用 “?”表示小朋友，很快就畫好了示意圖。

在教學中，剛開始學生還不是很會畫示意圖，這時教師可以根據學生們自身的特點，引導學生用簡單的符號、圖形來表示實物，比較簡單，且速度又快。經過長期訓練，學生的畫圖能力也會逐漸提升。

（二）示意圖過渡到線段圖

隨著學生年級的增高，解決問題的題目也復雜起來，而且數據也大了，如果還是用示意圖來解決就比較麻煩了，這時我們應該想到線段圖。線段圖在解決問題教學中起到了非常重要的作用，它可以幫助學生們學會解決復雜關系的問題。它既培養學生們的解題能力，又促進了學生們數學思維的發展，是一種十分有效的解決問題的教學方法。例如，二年級下冊《解決問題》中“比一個數多幾的解決問題”教學中有如下試題。

教師先讓學生獨立完成，學生完成后， 教師及時反饋這題。在反饋時，教師先讓學生自己數一數你畫了幾個?？并又問學生：“你是怎么數出來的？”接著，教師出示課件，問學生：“要使大家能很清楚地看出?比△多5個，可以怎么表示呢？”學生回答道：“在△和?同樣多的那部分那里用虛線把它們分開，后面剩下的5個就是比它多的5個。”這時，教師又問學生：“那我們有沒有更簡單的表示方法？”教師提示可用線段圖來表示。

教師先讓學生看上圖1，先畫一條線段，表示△的個數，并在線段上標明7個：接著畫一條和剛才一樣長的線段，把一樣多的部分用一樣長的線段來表示；最后多的5個?就是再畫一條稍微短點的線段，因為多的部分只有5個，還要在這線段上標上多5個，然后把圖形隱去，就是圖2這樣了。學生看了之后，很快就理解?比△多5個的含義了，他們也就知道該用什么方法來計算了。從這線段圖中，學生能很清楚地知道，?的前半部分的個數表示與△一樣多，也是7個，后半部分的個數是比△多的5個（相差數），也就是說?有兩部分組成，前半部分是7個（較大數），后半部分是5個（相差數），學生能很快根據“較大數-較小數=相差數”的關系，列出算式： 7+5=12（個）。如果教師不利用此線段圖，只讓學生從“?比△多5個”這句話中去理解，他們就很難理解△與?之間的關系，不清楚到底誰多，誰少？可能會有部分學生會這樣算?的個數“11-5=6（個）”。學生看了此線段圖后，就理解“?比△多5個”這數量關系了，他們也就不會出現“11-5-6 （個）”那樣去算?的個數了。從中教師讓學生了解了線段圖，并明白畫線段圖的好處。在練習中，教師還讓學生練習了看線段圖寫算式的練習題。

在二年級上冊教材中呈現出線段圖，我們可以從一年級漸漸開始滲透線段圖，從簡單題入手，這是培養學生畫圖能力的基礎。通過借助線段圖解題，可以化抽象為形象、直觀，這樣學生就能很好地理解圖意，能更好地發展學生的思維，而且為中高年級時學習相關的解決問題教學做好鋪墊作用。在教學中要鼓勵學生運用畫圖策略，并且逐漸地用示意圖、抽象的線段圖來解決問題，這樣他們解決問題的能力也會不斷提高。