解后而三思,直達學生數學思維本質
楊駿
摘 要:數學知識有著縱橫交錯的聯系,解題思路是靈活的,解題方法是多種多樣的。所以即使學生能一次把題目做對,解題方法也不一定是最好、最簡便的。所以,教師應該讓學生在做完題后,進一步學會反思。反思解題中的疏漏,思考解題思路和過程,讓學生創造性地去學習,去探索,去總結,從而在更高層次上開發解題智慧,提升思考力。
關鍵詞:小學數學 思維 反思
“數學問題的解決只是完成了學習的一半,更重要的是解題之后的回顧與反思。”解題后的反思是必不可少的重要環節,它能幫助學生總結經驗,發現規律,形成技巧,也能觸類旁通,有效地提高學習效率。為提高學生的解題能力,教師需提倡并訓練學生進行有效的解題反思。
一、思疏漏,確保思維密度
做完題后,為了保證解題的合理性和正確性,我們要積極反思,查漏補缺,歸納總結應注意的方面。如反思題目中隱含條件與答題是否有相抵觸的地方;是否還存在其他情形的可能;是不是掉進了命題人設下的陷阱里。以此來提高自己的分析能力,并對自己在答題中出現的錯誤加以改正。
案例1:長方形裁去一個角,剩余( )個角。
錯解: 3個角(4個角或5個角)。
正確答案可通過列表表示:
根據圖示可知,一個長方形裁去一個角,可出現三種情形。學生往往只會想到一種,教師在引導學生不斷思考、尋找準確答案的同時,還要給學生充分的探索時間和空間。
案例2:圖1是平行四邊形(單位:厘米),一條邊上的高是5厘米。它的面積是多少?
錯解:6×5=30(平方厘米)
這個解法是不對的。5厘米是平行四邊形中的哪個高,學生沒有給出正確判斷。
其實,圖中邊長為6厘米的底邊,不能以5厘米為高,而僅以邊長為4厘米的底邊為高,如圖2所示。如此,正確答案應為4×5=20(平方厘米)。
上面的例子告訴我們,要做到解題正確,審題、分析都很重要,還要有條理地思考。小學生的生理、心理特征往往會導致思考問題比較片面,就容易犯上述的錯誤。作為教師,要培養學生解題后反思的能力,及時“回頭看”,對解題的結果做一個總結。
二、思算法,提升思維廣度
(一)思方法,找規律
很多題目的解題思路是一樣的,學生通過解題后的反思總結出解決這類題目的方法,以后再碰到這一類的題目,就知道從哪個方面思考才不至于走彎路,解題的思路也能更清晰明了。學生領會了解題方法的實質,運用總結出的方法,就能解決同類型的習題,通過歸納整理,數學學習就變得更簡單了。
因此,我們要培養學生閱讀、分析題目的能力,尋找數學的本質問題,尋找規律,把一個復雜的問題分解成若干簡單的問題。解題后再進行回顧、梳理,把同類型的習題進行對比,找到共性的方法,然后再升華、提煉成解題方法,最后運用到以后的解題中去。教師引導學生養成這樣的習慣,長此以往,其數學基本功終將形成。例如,在基本的四則運算中,有些雖不是法則,但也有規律可循。
案例3:仔細觀察一下,下面的減法有什么特點?它們的差有什么規律?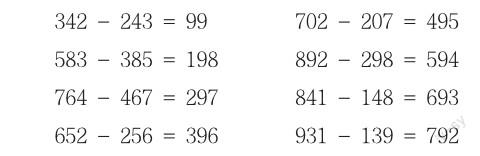
分析與解答:
(1)通過觀察,你發現上述算式中有怎樣的相同點呢?
(2)上面各題的差都是幾的倍數?分別是這個數的幾倍?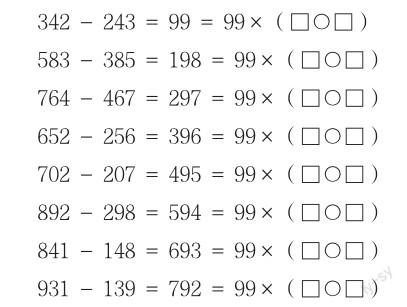
(3)上述題目中,前后算式有什么關聯嗎?
(二)思一題多解
新課標指出,要注重數學知識和方法的層次性和多樣性,采取螺旋式的方式,適當體現選擇性。因此,在數學解題的過程中,教師要鼓勵學生從不同的角度解題,衍生出更多的解題方法,提升學生數學學習的思維廣度和思辨能力。此外,還要培養學生在不同的解題方法中尋找最優解的能力,感悟數的運算的一致性。
我們由上述算式看出,盡管答案有很多種,從不同的角度可以填寫不同的數使算式成立,但都有其一致的基本方法,就是要先假設等式的結果,再根據不同的運算規律填寫。筆者認為,利用倒數的性質和0的特征可以快速答題,但是假設法和一致性兩種方法可以拓展學生思維的廣度,教師在講解時要抓住其本質特征,引導學生尋找多種方法。
教學中適當的一題多解,能激發學生的探究欲望,加深學生對所學知識的理解,訓練學生熟練運用數學思想和方法,拓展思維的廣度,使學生的思維素質得到培養,創造性思維得到發展。
班里學生的學習能力各不相同,教師要針對學生的這一特點,設計適當的開放性練習,使不同層次的學生都能找到適合自己的方法。在不同層次的解題思路中,教師通過點撥,對學生的數學思維進行優化、訓練,使其能夠選擇合理、簡明的運算策略進行解題,形成規范的思維品質。
(三)思算法多樣化
新課標指出:“由于學生生活背景和思考角度的不同,所使用的方法必然是多樣的,教師應尊重學生的想法,鼓勵學生獨立思考,提倡計算方法的多樣化。”“提倡算法多樣化”是數學課程標準的重要理念之一,其實質是尊重學生的個性發展,提倡個性化學習,支持和鼓勵學生在數學學習中用自己喜歡的、熟悉的、擅長的思維方式解決問題。
教師在課堂上要營造寬松的氛圍,給予學生更多思考和表達的機會,鼓勵學生在數學問題面前勇于嘗試,從多角度解決問題,并且能夠用自己的方法表達出來。同時,算法多樣化要區別于一題多解,比一題多解的要求低些。只要方法合理,學生表達清楚,教師就應該予以肯定和鼓勵,這是一種基于學生不同認知水平和個性的體現。
但應注意的是,在課堂教學中,教師要避免為了多樣化而多樣化,避免低級的多樣化,引導學生過濾無意義的方法。方法多樣化應該是基于發展學生思維水平的要求之上的,基于不同的認知水平,一些學生找不到富有個性的方法,這時也不要強求,要帶領這部分學生學習別人的方法。
三、思問題,挖掘思維深度
在數學教學中,如果教師還是停留在因“解”而“解”的階段,那么對于數學深度的挖掘是不夠的。教師對數學習題的講解不在多而貴在精,在講解一題時要有同類型、不同層次習題的儲備,解題后引導學生反思,深挖此類題的解法,追問同類型習題還可以往什么方向發展。比如把條件和題目修改一下,變成另外一個題目,同時把其他準備好的習題拿出來讓學生去思考,把更深的、更難的題目用已經總結好的方法去解決,把學生的思維層次挖得深一點兒,做到舉一反三。
綜上所述,我們要培養學生解后而三思的良好品質,要思疏漏、思算法、思問題,在思維品質的密度、廣度、深度上下功夫,培養學生的核心素養,使其會用數學的眼光觀察現實世界,用數學的思維思考現實世界,用數學的語言表達現實世界。
參考文獻
[1]斯苗兒.小學數學教學案例專題研究[M].杭州:浙江大學出版社,2005.
[2]張璽恩.中國著名特級教師教學思想錄(小學數學卷)[M].南京:江蘇教育出版社,1996.
[3]連林翟.小學數學優秀題解析[M].北京:北京教育出版社,1990.
[4]楊慶余.小學數學課程與數學[M].北京:高等教育出版社,2004.
[5]鄭毓信,肖柏榮,熊萍.數學思維與數學方法論[M].成都:四川教育出版社,2005.
[6]陶興模.注重培養學生解題后反思的習慣[J].中學數學月刊,2002(3).
[7]鄭建偉.談數學的反思式學習,培養學生的創新能力[J].數學教學研究,2011(9).
[8]吳衛東.對算法多樣化的理性思考[J].教學月刊(小學版),2003(2).

