認知策略在數學教學中的滲透

高冬雪 張丹

摘要：認知策略是一種重要的學習策略，學生在學習過程中有意識地選擇和調整思維方式，有利于提高記憶效率和思維品質。基于此，文章闡述認知策略的定義和分類，并通過舉例，詳細說明各種認知策略在教學中滲透的具體方法，以及滲透時應注意的問題。

關鍵詞：認知策略；數學教學；陳述性知識；程序性知識；過程性知識

一、認知策略的定義

認知策略至今還沒有統一的定義，但學者有一個共同的認識，即看重學習者對信息的加工和調節。筆者對認知策略進行定義，即學習對象內部組織而成的一種能調控學習、思維等活動的定向技能。

認知策略可以從兩個方面敘述：一是數學的思維方法，稱為策略性知識，二是個體對自己認知過程的認知，稱為反省認知或元認知。本文是從第二個方面討論認知策略。

在教學過程中，教師對認知策略內涵的理解和在教學中對認知策略的應用十分重要，而滲透認知策略的一個難點是教師如何在教學過程中潛移默化地向學生示范應用認知策略。

二、認知策略的類型

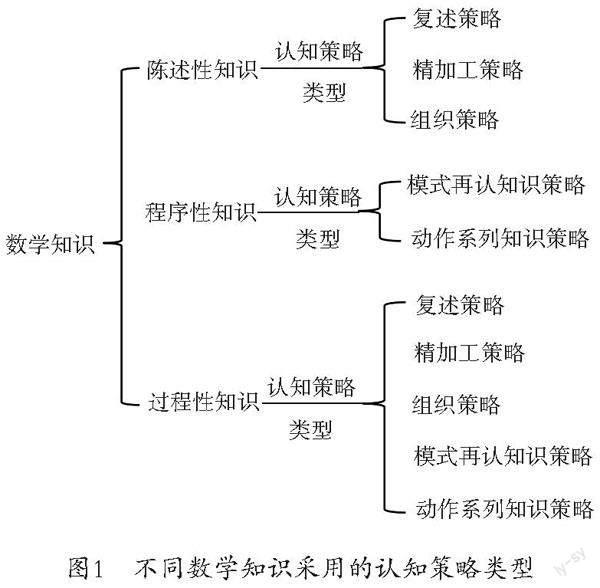
數學知識可以分為陳述性知識、程序性知識和過程性知識。針對不同的數學知識，認知策略也分為不同的類型。對陳述性知識，教師可以采用的認知策略有復述策略、精加工策略和組織策略；對程序性知識，教師可以采用的認知策略有模式再認知識策略和動作系列知識策略；過程性知識包含對陳述性知識及程序性知識獲得的體驗，其動態性貫穿于知識學習的全過程，因此以上認知策略對過程性知識都適用。圖1為數學知識的分類及針對各類知識應采用的認知策略類型。

（一）復述策略

復述策略是指為了記憶知識而將知識不斷復述，是一種最常用的記憶知識的策略，通常作為學習陳述性知識的策略。

（二）精加工策略

皮連生教授所說的“精加工”是指學習者為了記憶知識，將學習的項目與其他方面的材料建立聯系，一般作為促進陳述性知識學習的策略，以達到長期保持的目的，如想象、口述、總結、做筆記、類比、答疑等。常用的精加工策略有位置記憶法、首字聯詞法、關鍵詞法和視覺聯想法。

首先，位置記憶法。位置記憶法是學習者在腦海中建立一個場景，并將要記憶的內容與場景中固定位置的事物一一對應，回憶時就能按照位置提取需要的信息。

其次，首字聯詞法。首字聯詞法是為了記憶一系列知識點或某個過程的步驟，利用每個詞的第一個字形成一個完整的句子或者一個英文的縮寫。

再次，關鍵詞法。關鍵詞法是指在學習一種新知識時，可以通過聯想、諧音等方法，將其與某個關鍵詞聯系在一起，借助視覺表象來記憶。

最后，視覺聯想法。視覺聯想法是指將學習的知識與現實中的事物聯系在一起，這種聯系越奇特、越夸張，記憶就越牢固。

（三）組織策略

組織策略是將學過的知識納入有意義的類別，整理成有組織的結構，這樣在記憶、提取知識時，可以根據知識間的內在聯系和結構，更加高效地學習。常見的組織策略有歸類整理、提綱挈領、作圖示意、運用理論模型。

歸類整理是將所學的知識進行分類、整理，形成知識結構，有利于提高記憶效率，是學習中最常用的一種策略；提綱挈領是指用數字標記知識中的綱目、要點，形成一定的層次結構，通常運用于記憶信息量很大的知識，化繁為簡；作圖示意是指將知識用圖解的形式表示，通常用連線、箭頭、括號等輔助作圖，以表現出其內在結構；運用理論模型是指在遇到可遵循某個規律的過程時，運用符合其規律的理論模型，就可快速組織和整合信息。

（四）模式再認知識策略

模式再認知識策略是指對某個模式進行再次認識和分類的過程。比如，識別某個概念的一個新事例，或者識別符合某個行為的條件，或者符合應用某個規則的條件。

（五）動作系列知識策略

動作系列知識策略是指是為了完成某個過程，采取一系列步驟或認知動作，如數列求和方法中的錯位相減求和法。

三、認知策略在數學教學中的滲透策略

（一）陳述性知識對應的認知策略

數學教學中需要記憶的陳述性知識有很多，如定義、定理、解題步驟等。下面，筆者以等差數列概念的講解、奇函數相關性質的梳理、點的軌跡方程的求解步驟為例，介紹認知策略在陳述性知識教學中的滲透。

1.在等差數列概念的講解教學中滲透復述策略和精加工策略

等差數列的概念為“一般地，如果一個數列從第二項起，每一項與它的前一項的差都等于同一個常數，那么這個數列就叫等差數列，這個常數叫作等差數列的公差，常用字母d表示”。教師可以舉幾個例子，讓學生觀察規律，然后給出概念，并利用復述策略，讓學生將概念抄在筆記本上，加深印象。接著，教師利用精加工策略中的批注，將概念中需要注意的地方畫出來并標注原因。

具體畫線內容與原因如下：在等差數列的概念中，從第二項起畫線，因為后面是要與前一項作差，若是從第一項開始，則不存在前一項，教師強調教科書這樣表述是為了概念的嚴謹；每一項與前一項的差畫線，因為需要注意作差的順序，是“后面減前面”；常數畫線，常數就是前面說的差，而這些差相等，因此叫作公差。最后，教師運用復述策略，讓學生讀幾遍，并隨機提問。

教師要求學生畫線、標注的過程，就是在向學生滲透認知策略中的復述策略和精加工策略的過程。在這樣的概念教學過程中，學生學習會更加容易，記憶也更加清晰。

2.在奇函數相關性質的梳理教學中滲透組織策略

復習課中常見的一個環節是教師幫助學生梳理某一部分內容，如奇函數的定義及相關性質。教師先引導學生思考奇函數的相關知識，再引導學生將其展開。雖然教師的講述邏輯清晰，但對大部分學生來說，直接用言語敘述并不能產生較深的印象。因此，教師可以運用組織策略中的作圖示意策略，將奇函數相關知識間的關系用圖表示出來，讓學生在頭腦中形成形象記憶。如圖2所示。

3.在點的軌跡方程的求解步驟教學中滲透精加工策略和組織策略

高中階段常常遇到求點的軌跡方程問題。如有這樣一道例題：等腰三角形頂點為A（4，2），底邊的一個端點為B（3，5），求另一個端點的軌跡方程。

解題第一步要建立一個平面直角坐標系，但此題已經有坐標系，故第一步可以省略；第二步，設另一個端點為C（x，y）；第三步，找到限制條件，這道題的限制條件為三角形是等腰三角形，故|AC|=|AB|；第四步，將限制條件用點坐標表示，即=

；第五步，化簡得（x-4）2+（y-2）2=10，所以另一個點的軌跡為圓。

教師隨后總結步驟：第一步，建立平面直角坐標系；第二步，設點坐標；第三步，限制條件；第四步，代入點坐標；第五步，化簡。但若就此結束，學生印象便不深刻，所以教師可以利用精加工策略中的首字聯詞法，將五個步驟中的第一個字連在一起，組成“建設現代化”這個短語。但是，如何在遇到求點軌跡方程問題時想到“建設現代化”這個短語呢？方法如下：教師利用精加工策略中的視覺聯想法，把點在平面直角坐標系中運動的軌跡比喻為某城市的發展規劃圖，涉及城市未來的發展，學生就會聯想到建設現代化的城市。最后，教師可以強調，這五個步驟是求點的軌跡方程問題通用的步驟，可以作為一個理論模型，下次再碰到此類問題時可以直接套用，這個強調的過程其實是教師在滲透組織策略中的運用理論模型。

（二）程序性知識對應的認知策略

程序性知識以產生式系統為代表。解決數學問題的過程就是一個產生式系統，由條件推出一個子目標，再將該子目標作為條件去推出第二個子目標，以此類推，最后達到問題的總目標。一個人頭腦中儲存了解決不同問題的產生式系統，就能夠自如地處理相關事情，解決相關問題。解決數學問題的關鍵在于能否構建相應的產生式系統，因此教師滲透認知策略就是幫助學生形成一個又一個數學問題的產生式系統。

下面，筆者以數列問題為例，介紹認知策略中的動作系列知識策略在數學教學中的滲透。

“已知數列{an}的前n項和Sn，若4Sn=（2n-1）an+1+1，且a1=1。求證：數列{an}為等差數列。”教師通過提問引導學生思考，由題中的各個條件能推出什么？學生自然會注意到an與Sn的關系式。教師再引導學生回顧an與Sn關系的相應知識點，學生自然想到an=Sn-Sn-1，即將原式中所有的n都換成n-1，構成一個新式子，再相減，得到一個關于{an}的遞推公式。這道題顯然利用了等差數列的定義來證明，即每一項與前一項的差為一個常數。

教師由已知條件引導學生能推出什么，再由推出的知識作為條件繼續推出其他知識，這個過程就是在幫助學生構建產生式系統，其中運用到了動作系列知識策略，避免了無方向的思考，大大縮短了解決問題的時間，也提高了準確率。

值得注意的是，教師在講解中滲透認知策略時要注意過渡自然，這樣才能使認知策略在無形中滲入課堂，增強教學效果。

認知策略在陳述性知識和程序性知識教學中的應用十分廣泛，并且常常是多種認知策略共同應用，合理地運用認知策略會使學生在數學學習中事半功倍，減輕學生的壓力。因此，認知策略滲入高中數學教學非常必要。

參考文獻：

[1]張大均.教育心理學[M].北京：人民教育出版社，2003.

[2]張志淼.數學學習與數學思想方法[M].鄭州：鄭州大學出版社，2006.

[3]戴永.高中數學命題的教學策略研究[D].天津：天津師范大學，2006.

[4]周朝霞.高中生數學認知策略培養研究[D].蘭州：西北師范大學，2018.

[5]宋健棟.高一學生數學學習策略調查研究[D].煙臺：魯東大學，2017.

[6]華晶.培養高中生數學學習策略的個案研究[D].上海：上海師范大學，2021.

[7]溫淳.高中數學學習策略與教學研究[D].長春：東北師范大學，2007.

（作者單位：長春師范大學）