精瞄問題設計，靶向素養提升

王娟 崔豪東

［摘? 要］ 數學教學應聚焦邏輯關聯問題，讓學生經歷推理思辨過程，體會幾何內涵意蘊，形成數學理性思維，從而培育數學關鍵能力，提升學科核心素養.

［關鍵詞］ 問題鏈；邏輯關聯；理性思維；關鍵能力

數學教學應強調問題性，以問題引導學生學習. 章建躍博士說：“教師要在知識形成過程的‘關鍵點’上，在解題策略的‘關節點’上，在知識間聯系的‘聯結點’上，在數學問題變式的‘發散點’上，在學生思維的‘最近發展區’內提出問題、提好問題，培養學生問題意識，孕育學生理性精神. ”

問題鏈是指具有系統性的一連串的數學問題，問題鏈教學應重在設計一組邏輯關聯的問題，旨在引發學生的連續思維，實現學生的素養提升. 下面筆者以2021年南京市初中數學基本功大賽課堂教學評比環節的教學內容——人教版八年級數學“12.3? 角的平分線的性質”為例，芻談對問題鏈教學的實踐與思考.

教學實踐

1. 以感知為鏡，萌生知識樹

問題1：請談談你對角的平分線的認識.

學生對角的平分線有不同層次的認識. 如：角的平分線是一條射線，它把一個角分成相等的兩個角；把一個角沿著角的平分線翻折，角的兩邊能夠完全重合.

教學說明：本環節約2分鐘，教師拋出問題，學生積極發言、相互補充.

2. 育創新之思，延拓思維鏈

問題2：在紙上任意畫一個角，嘗試用不同的方法作出這個角的平分線.

生1：我是用量角器作圖的.

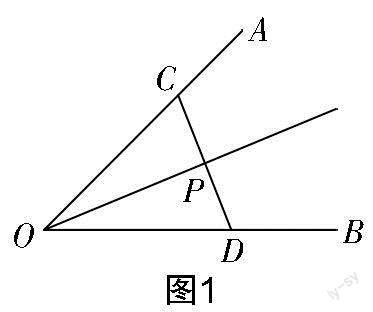
生2：我是用刻度尺作圖的. 如圖1所示，在OA，OB上分別取點C，D，使OC=OD，連接CD，取CD的中點P，作射線OP，則OP即為所求.

生3：我也是用刻度尺作圖的. 如圖2所示，在OA上取C，E兩點，在OB上取D，F兩點，使OC=OD，OE=OF，連接CF，DE交于點P，作射線OP，則OP即為所求.

追問：還有用其他作圖工具的嗎？

生4：我是用三角尺（含有刻度，可度量長度）作圖的. 如圖3所示，在OA，OB上分別取點C，D，使OC=OD，過點C作CE⊥OA，交OB于點E，過點D作DF⊥OB，交OA于點F，CE和DF交于點P，作射線OP，則OP即為所求.

生5：我也是用三角尺作圖的.如圖4所示，在OA，OB上分別取點C，D，使OC=OD，作∠OCE=60°交OB于點E，作∠ODF=60°交OA于點F，CE和DF交于點P，作射線OP，則OP即為所求.

追問：如果只用無刻度直尺和圓規，如何作出這個角的平分線？

生6：如圖5所示，作OC=OD，OF=OE，且C，F兩點均在OA上，D，E兩點均在OB上，連接CE，DF交于點P，作射線OP，則OP即為所求.

生7：如圖6所示，作OC=OD，且點C在OA上，點D在OB上，任作CE交OB于點E，作∠ODF=∠OCE交OA于點F，CE和DF交于點P，作射線OP，則OP即為所求.

生8：我是逆向思考的，我先畫出角的平分線，然后研究角平分線帶來的結論，想到了一種作法. 如圖7所示，作OC=OD，且點C在OA上，點D在OB上，再分別以C，D為圓心，大于CD的長為半徑作弧，兩弧交于點P，作射線OP，則OP即為所求.

生9：我先畫出角的平分線和OB邊的一條平行線，然后就有了靈感. 如圖8所示，在OA上取點C，作∠ACD=∠AOB（兩角在OA同側），作CO=CP交CD于點P，作射線OP，則OP即為所求.

教學說明? 本環節約10分鐘，學生主動參與活動，先自主思考，再小組討論，教師則巡視并指導、傾聽并啟發，最后學生踴躍展示.

3. 行探索之途，貫通一條線

問題3：在∠AOB的平分線上任取一點P，分別作點P到OA，OB的垂線段PM，PN，你有什么發現？

學生作圖后一致認為PM=PN.

追問：能證明你的發現嗎？

生10：我是用刻度尺度量的. 如圖9所示，度量可知P1M1=P1N1，P2M2=P2N2，P3M3=P3N3.

生11：我是用翻折法說理的. 把∠AOB沿著它的角平分線翻折，角的兩邊能夠完全重合（在同一條直線上），依據“過一點有且只有一條直線與已知直線垂直”，可得PM=PN.

生12：我是用全等法證明的. 如圖10所示，可由“AAS”證得△POM≌△PON，于是得到PM=PN.

學生探究后得出角的平分線的性質定理——“角平分線上的點到角兩邊的距離相等”.

問題4：在角的內部找點，使得該點到角兩邊的距離相等（盡可能多找一些點）.

追問：類比前面的探究，你能提出什么問題？你能證明嗎？

學生多找一些點后自然而然提出問題“證明這樣的點都在角的平分線上”，然后進入分析問題和解決問題的過程中. 學生把習得的基本活動經驗付諸實踐，呈現了量角器度量、翻折法說理和全等法證明（HL）3種方法. 學生在總結結論時，對“角的內部”進行了思辨，直到一位學生舉出反例才使得所有同學平息爭論，最后學生一致得出角的平分線的性質定理的逆定理——“角的內部到角兩邊的距離相等的點在角的平分線上”.

教學說明? 本環節約20分鐘，學生主動參與活動，在探索中發現，然后舉手搶答. 證明時，學生先自主思考，再小組討論，最后爭相展示. 教師組織學生展示并相互評價、激烈辯論.

4. 以應用為標，聯結知識網

問題5：如圖11所示，△ABC的角平分線BM和CN交于點P. 你能得出哪些結論？

教學說明? 本環節約10分鐘，學生主動參與活動，自主思考后舉手回答，教師傾聽并啟發，規范其說理過程，板書關鍵證明步驟.

5. 借知識輸出，建筑素養域

問題6：你學到了什么？（知識、方法和思想等）

學生積極分享學到的知識和獨特的領悟. 有學生總結出幾何定理的研究方法是“探索—猜想—證明—應用”，有學生領悟出幾何證明的解題方法是“從條件出發正向思考”和“從結論出發逆向思考”，還有學生發現課堂中蘊含類比思想.

教學說明? 本環節約3分鐘，學生舉手發言、相互補充，教師客觀評價并引導學生向方法、思想方面去深層思考.

教學思考

1. 聚焦邏輯關聯，建構聯結體系

邏輯關聯是事物因變化產生的關聯. 數學問題的邏輯關聯，包括知識技能關聯、思維方法關聯和數學素養關聯. 在構建問題鏈時，教師既要著眼整體架構，又要緊扣內容本身，還要關注方法素養，思索內容、方法和素養的聯結點. 在本節課的教學中，6個問題構成有一定梯度和邏輯結構的主問題鏈. 從談認識到說發現，從證發現到得結論，再到聊收獲，由感知到深入，知識中蘊含方法，方法中夾雜思想，整條鏈是一個聯結體系.

2. 凸顯推理思辨，發展理性思維

《義務教育數學課程標準（2022年版）》指出：“推理能力有助于逐步養成重論據、合乎邏輯的思維習慣，形成實事求是的科學態度與理性精神. ”選擇問題時，教師要甄選能凸顯推理能力、能啟發學生思辨的關鍵問題. 在本節課教學中，問題多以“認識”“發現”“思考”“感受”等方式呈現，能適度啟發學生的數學思維，能引導學生思考和探索，能使學生經歷觀察、實驗、猜測、推理、交流、反思等理性思維的基本過程.

3. 深化內涵意蘊，培育關鍵能力

對于問題鏈的核心問題，教師要采用追問等形式，從其橫向拓寬維度、縱向挖掘深度，衍生出子問題鏈，驅動學生深度學習，在思考中實現元認知，在探究中生成關鍵能力. 搭建子問題鏈時，教師要選擇能深化內涵、導向意蘊的問題. 在本節課教學中，問題2和兩個追問貫通了一條子問題鏈，核心問題的豐富內涵得以彰顯，問題4和一個追問作為子問題鏈將學生思維導向橫向遷移，學生在深度思考中提升了關鍵能力.