問題驅動　變中求本　積累經驗

楊磊

摘? ?要：在數學教學中，問題是教學的出發點，也是驅動學生積極思考、推動課堂教學的有效載體。《義務教育數學課程標準（2022年版）》強調通過合理設計探究問題促進數學教學活動的開展。教師在教學中重視在學生的認知起點和最近發展區設計有思維含量、有層次、有梯度的問題鏈，促進學生思維從無序向有序提升，從點狀水平向結構化水平提升，從而促進學生深度思考和深度學習，探尋學科本質，感悟數學思想方法，積累數學活動經驗。

關鍵詞：小學數學；問題驅動；變中求本；積累經驗

中圖分類號：G623.5? ?文獻標識碼：A? ?文章編號：1009-010X（2023）28-0016-05

一、課前思考

“探索乘積最大的規律”是冀教版小學數學四年級下冊第九單元探索樂園的教學內容，目的是讓學生在用不同的數字組數探索怎樣組數乘積最大或最小規律的過程中，體會乘法運算中有許多奧秘，發展數感。研讀教材時，重點做了以下幾點思考。

問題一：學生的起點在哪里？

學習本課之前，學生已經掌握了三位數乘兩位數的筆算方法、積的變化規律、乘法的估算、乘法運算定律等知識，并且對于探索規律類的學習內容有一定的數學活動經驗。通過前測調研發現，用5個數字組乘積最大的三位數乘兩位數的乘法算式，90%以上的學生沒有頭緒，思考處于無序的狀態。后來改用4個數字組乘積最大的兩位數乘兩位數的乘法算式進行前測調研發現，60%左右的學生能想到這兩個乘數的首位數字都要盡可能大，但后面的個位數字如何確定仍有困難。

問題二：如何選擇研究的載體和素材？

教材中的問題是“用2、3、4、5、6五個數字組成一個三位數和兩位數。怎樣組數可使兩個數的乘積最大？要使兩個數的乘積最小，該怎樣組數？”通過前測調研發現，如果直接研究五個數字組乘積最大的三位數乘兩位數的問題，超出了大部分學生的最近發展區。基于學生的認知基礎對教材進行教學法的加工，可以先退到研究四個數字或三個數字組乘積最大乘法算式的問題尋找規律，再研究五個數字的問題，會更順應四年級小學生的認知特點。由于課上時間有限，教師應重點研究三個數字、四個數字、五個數字組乘積最大乘法算式的規律，將組乘積最小算式的規律放在課后拓展延伸完成。

基于以上的思考，確定本課的教學目標是：

1.會用三個數字、四個數字、五個數字組成乘積最大的乘法算式。

2.通過探索乘積最大算式規律的數學活動，感悟分類、數形結合、以退為進、轉化等數學思想方法，發展數感、推理意識、模型意識等。

3.在探索規律的過程中，感受數學的有趣和神奇，激發學習數學的興趣。

本課的教學重點在于能探索乘積最大算式的規律。教學難點是感悟分類、數形結合、以退為進、轉化等數學思想方法，發展數感、推理意識、模型意識等。

二、教學過程

（一）提出問題孕伏鋪墊

1.創設情境提出問題

師（出示）：用2、3、4、5、6五個數字組成一個三位數和兩位數。怎樣組數可使兩個數的乘積最大？（學生嘗試解答大約3分鐘，教師巡視）

師：剛才老師發現大部分同學似乎遇到了困難，誰來說說你感覺難在哪里？

生：用這五個數字組成的三位數乘兩位數的乘法算式有很多個。不容易確定到底哪個算式的乘積最大。

⒉啟發思考，以退為進

師：是的，在這里遇到了困難，怎么辦呢？讓我們看看前人的智慧能否給我們些啟發？

出示：天下難事，必作于易。——老子

復雜的問題要善于“退” ，足夠的“退”，退到最簡單而不失去重要性的地，是學好數學的一個訣竅。——華羅庚

師：老子和華羅庚先生的這兩句話英雄所見略同。遇到復雜的、困難的問題，要退到簡單的地方思考以獲得啟發。五個數字的問題對我們來說似乎有難度了，退到哪里，就容易了呢？

生1：四個數字。

生2：三個數字。

生3：二個數字。

師：哈哈，如果退到二個數字就不用研究怎樣組乘法算式了，可以先退到比較簡單的三個數字的問題思考。

⒊化難為易，嘗試解決

出示：用4、5、6三個數字組成一個兩位數和一位數。怎樣組數，可使兩個數的乘積最大？

（）（）×（）

師：猜一猜，哪個算式的乘積最大？

生1： 64×5。

生2： 65×4。

生3： 54×6。

師：同學們為什么不猜4□×□呢？

生：如果乘數比較小，乘積也就比較小。

師：好的，在剛才的幾種猜想中我們先來研究一下65×4。65×4≈70×4=280，把65估大了，乘積才是280。同學們也可以估算一下另外兩個算式的乘積。

生1： 64×5≈60×5=300。

生2： 54×6≈50×6=300。

師：另外的兩個算式都是把數估小乘積是300，準確的乘積肯定要大于300。為什么65很大，它和4搭配組成的乘法算式的乘積卻不是最大的呢？

生3： 4比較小。

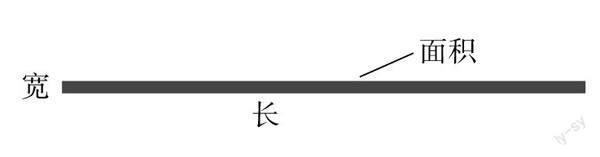
師：在乘法算式中，兩個乘數共同決定著乘積的大小。就像長和寬共同決定著長方形的面積，如果只考慮了長，而不管寬，那樣面積不會大。同樣的，如果只想著一個乘數盡可能大，而忽視了另一個乘數，乘積也不大。

師：64×5和54×6到底誰的乘積最大呢？

學生嘗試計算：

生1： 64×5=320，54×6=324。

師：剛才大部分同學猜想64×5的乘積更大，而實際算出結果后卻是54×6的結果更大，這是怎么回事呢？

生1：剛才估算的時候：64×5≈60×5=300，少算了4個5，如果再加上這4個5就是320；54×6≈50×6=300，少算了4個6，如果再加上這4個6，就是324。

師：同學們，能理解他的想法嗎？我們可以聯系乘法算式的意義來理解。

６４×５

＝（６０＋４）×５

＝６０×５＋４×５

５４×６

＝（５０＋４）×６

＝５０×６＋４×６

師：4放在6的后面組乘法算式，比300多算4個5；4放在5的后面組乘法算式，比300多算4個6。

師：解決了三個數字組乘積最大的兩位數乘一位數的問題，回顧一下，你有什么竅門嗎？

生：讓最大的數字自己做一位數，讓第二大和第三大的數字組成一個比較大的兩位數，它們的乘積最大。

【思考】本環節重點啟發學生遇到困難的、復雜的問題學會退到簡單的地方開始思考，為后面解決復雜問題積累數學活動經驗。

（二）繼續追問深入探究

1.提出問題

師：有了前面研究的基礎，同學們現在能進一步研究四個數字的問題了嗎？

生：可以。

出示：用3、4、5、6四個數字組成兩個兩位數。怎樣組數，可使兩個數組的乘積最大？

2.分析問題

師：在組乘法算式的時候首先應該考慮什么？

生：讓這兩個乘數都盡可能大。需要先確定首位數字，盡量大。確定首位數字分別是6和5。

師：首位數字6和5確定之后，再和剩下的3和4搭配，組成的乘法算式有幾種可能性？

生：64×53和63×54。

師：你覺得哪個算式的乘積最大呢？

生1：64×53乘積最大。

生2：63×54乘積最大。

師：到底哪個算式乘積最大，怎樣能讓大家信服呢？

生：計算出結果。

（學生計算驗證：53×64=3392、54×63=3402）

3.理解原理

師：如果不計算出結果，你知道哪個算式的乘積最大嗎？

生：54與63的差更小，它們的乘積更大。

師：你是怎樣想到這個方法的？

生：三年級的時候，我們研究過長方形周長不變的時候，長和寬的差越小面積越大，這個問題與那個問題相似。

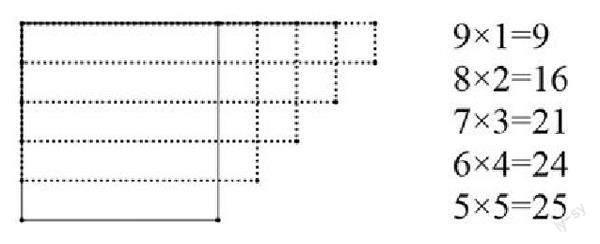
師：是的，這位同學聯想到三年級長方形的研究，當長方形的周長不變（也就是長與寬的和不變）時，長與寬的差越小，長方形的面積越大。

（幾何畫板動態演示）

師：在這里，可以應用這個規律來解釋。除此之外，我們也可以聯系乘法算式的意義來理解。

６４×５３

＝（６３＋１）×５３

＝６３×５３＋１×５３

５４×６３

＝（５３＋１）×６３

＝５３×６３＋１×６３

師：也可以借助圖形來幫助理解，電腦課件演示。比較兩邊的算式發現，64×53與54×63結果是相同的，1×53<1×63，所以54×63的乘積最大。

⒋變式練習

師：如果把這四個數字變一變，同學們還會思考嗎？

出示：用8、5、6、3四個數字組成兩位數和兩位數。怎樣組數，可使兩個數的乘積最大？

（）（）×（）（）

學生嘗試組乘法算式，師生交流：

師：誰來說一說你是怎么想的？

生：先考慮首位數字，把大的數字8和6放在首位。

師：首位確定后，考慮第二位有幾種情況？

生：85×63， 83×65。

師：如果不計算出得數，你能快速判斷出誰的乘積最大嗎？

生：83×65。

師：怎么想的呢？

生1： 83×65的差更小，所以它們的乘積更大。

生2：也可以聯系乘法算式的意義理解，比較大小。

８５×６３

＝（８３＋２）×６３

＝８３×６３＋２×６３

８３×６５

＝８３×（６３＋２）

＝８３×６３＋８３×２

師：四個數字組成乘積最大的兩位數乘兩位數的乘法算式，有什么共同的規律呢？

生：把最大的數字和最小的數字搭配組成一個兩位數，再把另外2個數字搭配組成一個較大的兩位數。

【思考】本環節引領學生探索四個數字組成乘積最大的兩位數乘兩位數算式，發展學生的理性思維，知其然知其所以然。

（三）拓展結構回歸本原

1.提出問題

師：剛才的幾個問題同學們解決得不錯，下面敢不敢迎接新的挑戰？

出示：用3、5、6、4、2五個數字組成一個三位數乘兩位數的乘法算式（每個數字只能用一次）。怎樣組數，乘積最大？

（）（）（）×（）（）

師：這個問題和剛才四個數字組乘法算式的問題相比較，什么相同？什么不同？

生：相同點都是組乘積最大的算式，不同點是多了一個數字2，由兩位數乘兩位數變成了三位數乘兩位數。

2.小組合作全班交流

師：多了一個數字2怎么辦呢？請同學們先獨立思考嘗試解決，然后小組內討論交流你的想法。（大約5分鐘）

師：哪個小組先來匯報一下你們的想法？

生：前面四個數字的問題已經討論過了，3、5、6、4四個數字組成63×54乘積最大，剩下重點研究2放在哪里就可以了。

生：2可以放在63或54的后邊，組成632×54或63×542。

師：632×54和63×542到底誰的乘積最大？如果不計算出結果你能判斷出，哪個算式的乘積最大嗎？

生：542與63的差更小，所以它們的乘積更大。

師：這位同學的想法，你們同意嗎？

（一部分同學同意，另一部分同學不置可否）

師：實際上剛才的那個規律是有前提條件的，前提條件是當兩個數的和確定不變，結論是這兩個數的差越小，乘積越大。仔細研究這里能夠發現632×54和63×542，算式中的兩個數的和變化了，已經不滿足那個規律的前提條件了，所以這里就不能應用那個規律。這條路走不通了，我們需要及時調整思考方向，還有其他的辦法嗎？

生：我們用計算器算出了結果632×54=34128

63×542=34146，63×542的乘積最大。

師：仔細觀察算式，能試著解釋其中的原理嗎？

生：仔細觀察比較這兩個算式632×54和63×542，能發現主要是2的位置發生了變化，2的位置變化就導致數的意義變了，乘法算式的意義也變了，可以從乘法算式的意義來理解。

６３２×５４

＝（６３０＋２）×５４

＝６３０×５４＋２×５４

６３×５４２

＝６３×（５４０＋２）

＝６３×５４０＋６３×２

師：觀察比較左右兩邊的算式你發現了什么？

生：630×54和63×540的結果是相等的，2×54< 63×2，所以 632×54<63×542。

師：5個數字，組成一個三位數乘兩位數的乘法算式，怎么組數乘積最大呢？

生：先不管最小的數，退到4個數字的情況思考，再把最小的數放在較小的兩位數后邊。

【思考】本環節回歸本原問題放手讓學生進行獨立思考、小組合作，分析并解決問題。

（四）課堂小結

師：學習到這里，讓我們一起回顧下這節課是怎樣探索組成乘積最大乘法算式規律的？

生：先研究了三個數字、四個數字組成乘積最大算式的問題。

師：接下來我們研究了什么問題？

生：接下來研究了五個數字組成乘積最大算式的問題。

師：遇到困難的時候，我們是用什么方法解決的？

生：五個數字的問題比較難，先“退”到三個數字、四個數字的問題來思考。

師：用三個數字、四個數字、五個數字組乘積最大算式共同的方法是什么？

生：都是把最大的數字分別放在2個乘數的最高位上，然后再思考剩下的數字怎樣搭配。

師：研究到了這里，大家覺得下面我們還可以研究什么問題？

生1：六個數字、七個數字組成乘法算式，怎么組數乘積最大？

生2：怎樣組乘積最小的算式呢？

師：看來同學們有很多有價值的思考，大家有基本的思路嗎？

生1：最大的數字要放在最高位上，再考慮其他數字的搭配。

生2：復雜的問題退到簡單的地方思考。

生3：組乘積最小的算式就是反過來想。

師：課后我們可以繼續探索這些新問題。

【思考】本環節重點引領學生回顧組成乘積最大算式的數學思想方法，并啟發學生聯想到新的數學問題，課后拓展延伸。

三、教后反思

像“探索乘積最大的規律”這樣的探索規律的教學內容需要讓學生充分經歷觀察比較、猜想驗證、歸納概括、解釋原理的過程，使學生最終實現數學思維的提升。回顧整節課的教學，有以下幾點思考和感悟。

（一）順應學生認知特點，解決學生的真問題

探索樂園的教學內容對小學生來說往往思維難度較大，教師需要對教材進行教學法的加工。探究的問題要突出數學的本質，有思維含量，解決學生的真問題。學習過程采用探索發現式學習與有意義的接受式學習相結合，可以有效的突破難點。在一次次“跳一跳摘果子”的過程中，學生的數學思維得到較好的發展，體會到數學思考的樂趣。

（二）運用數學思想方法，促進學生的真學習

探索乘積最大規律的學習過程中綜合運用分類、轉化、數形結合、以退為進等多種數學思想方法，發展了推理意識、模型意識等。通過探究一組問題，打通一類問題，為今后解決復雜問題積累了豐富的思維活動經驗，促進學生深度思考，讓學習真實發生。

（三）發揮數學育人價值，助力學生的真發展

在學習的過程中學生不僅著眼于具體的小規律，更加重視使學生領會數學的基本思想，形成研究問題的基本能力。在學習的過程中學生潛移默化感悟到數學的研究對象在變，思想方法不變，研究套路不變，體會到數學內在的力量。在學習的過程中，學生經歷問題解決的全過程，理解和掌握數學思想方法，提升了數學核心素養。

【責任編輯 王? ?悅】