基于核心素養的“三角函數的周期性”概念教學策略

惠敏敏

摘? 要：概念是數學的細胞，也是數學思維活動的重要載體。因此，數學概念教學不能止步于讓學生熟悉概念、運用概念解題，而應挖掘數學概念的內涵與外延。厘清新授概念與學生熟悉的數學概念、知識間的內在聯系，進而創建合適的數學概念生成情境，讓數學概念在學生的自主探究中主動生成;讓學生習得數學抽象、邏輯推理的具體方法，提升學生的數學核心素養。文章以“三角函數的周期性”公開教學觀摩課為例，闡述了數學概念教學中設計探究生成過程的重要性。教師應注重從真實情境出發，逐步引導學生感悟、體會，從而水到渠成掌握數學知識概念。

關鍵詞：三角函數;數學核心素養;教學策略;概念教學

一、教材分析

“三角函數的周期性”是蘇教版（2019版）高中數學必修第一冊教材7.3“三角函數的圖像和性質”的第一節內容。周期性是三角函數的一個典型特征，是后續研究及學習三角函數的圖像與性質的基本工具，三角函數周期性的研究也為一般函數周期性的研究奠定了重要基礎。

二、學情分析

該堂課是在學生已經學習了函數、角與弧度、三角函數概念等相關知識的基礎上開展的。學生來自江蘇省四星級高中的普通班，數學學習的基礎較好，且在高中階段的學習已經接近一個學期，數學思維能力有了很大的提升，已具備一定的自主探究能力、數學推理能力及數學抽象能力，可以借助已學知識，采用類比、化歸等思想方法完成本節課內容。

三、教學目標

其一，知識與技能。（1）了解周期函數的概念;（2）會判斷一些簡單的、常見的函數的周期性;（3）會求一些簡單的三角函數的周期。

其二，過程與方法。通過眾多實例總結探究周期函數，再由周期函數到三角函數的周期性的探索過程，培養學生的數學發現能力和概括總結能力。在研究周期性的過程中，讓學生體驗由簡單到復雜，由特殊到一般的化歸思想，并滲透數形結合的思想方法，培養數學的探索能力，學習鉆研精神和科學的認知態度，通過小組合作學習培養學生團結協作的精神，體現立學課堂的教學思想.

其三，情感態度與價值觀。通過家鄉本土的實例引入，培養學生熱愛家鄉，熱愛祖國的情懷。通過各種實例，提煉出共同特性——周期，體會事物間的內在聯系，感受類比、化歸的思想方法。在探索過程中體會失敗與成功的情感體驗。

其四，核心素養。以函數與三角函數的基本知識和基本技能為載體，培養學生的數學思維，讓學生逐步體會到用數學的眼光去觀察世界，用數學的思維來思考世界，用數學的語言來表達世界。在探究周期性和周期函數的概念過程中培養學生數學抽象能力;在由周期特征的實例與已有知識儲備函數性質（例如函數奇偶性的概念）的表述中，表示出周期函數的數學語言，培養學生的邏輯推理能力;借助單位圓、三角函數線直觀圖，培養學生直觀想象能力。

四、教學過程

（一）教學環節1：創設情境，引入新課

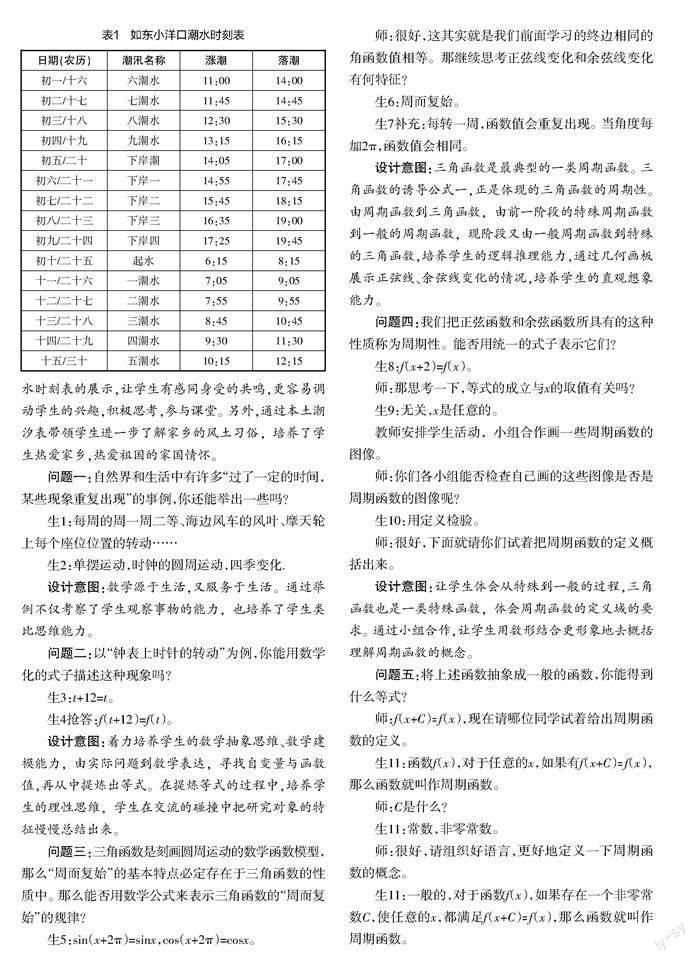
教師導入情境，如表1所示。

設計意圖：不少本地學生在小學和初中時，通過在社會實踐基地的學習，對潮水漲落有一定了解，而且有不少學生還有過趕海的經歷。通過如東本土小洋口潮水時刻表的展示，讓學生有感同身受的共鳴，更容易調動學生的興趣，積極思考，參與課堂。另外，通過本土潮汐表帶領學生進一步了解家鄉的風土習俗，培養了學生熱愛家鄉，熱愛祖國的家國情懷。

問題一：自然界和生活中有許多“過了一定的時間，某些現象重復出現”的事例，你還能舉出一些嗎？

生1：每周的周一周二等、海邊風車的風葉、摩天輪上每個座位位置的轉動……

生2：單擺運動，時鐘的圓周運動，四季變化.

設計意圖：數學源于生活，又服務于生活。通過舉例不僅考察了學生觀察事物的能力，也培養了學生類比思維能力。

問題二：以“鐘表上時針的轉動”為例，你能用數學化的式子描述這種現象嗎？

生3：t+12=t。

生4搶答：f（t+12）=f（t）。

設計意圖：著力培養學生的數學抽象思維、數學建模能力，由實際問題到數學表達，尋找自變量與函數值，再從中提煉出等式。在提煉等式的過程中，培養學生的理性思維，學生在交流的碰撞中把研究對象的特征慢慢總結出來。

問題三：三角函數是刻畫圓周運動的數學函數模型，那么“周而復始”的基本特點必定存在于三角函數的性質中。那么能否用數學公式來表示三角函數的“周而復始”的規律？

生5：sin（x+2π）=sinx，cos（x+2π）=cosx。

師：很好，這其實就是我們前面學習的終邊相同的角函數值相等。那繼續思考正弦線變化和余弦線變化有何特征？

生6：周而復始。

生7補充：每轉一周，函數值會重復出現。當角度每加2π，函數值會相同。

設計意圖：三角函數是最典型的一類周期函數。三角函數的誘導公式一，正是體現的三角函數的周期性。由周期函數到三角函數，由前一階段的特殊周期函數到一般的周期函數，現階段又由一般周期函數到特殊的三角函數，培養學生的邏輯推理能力，通過幾何畫板展示正弦線、余弦線變化的情況，培養學生的直觀想象能力。

問題四：我們把正弦函數和余弦函數所具有的這種性質稱為周期性。能否用統一的式子表示它們？

生8：f（x+2）=f（x）。

師：那思考一下，等式的成立與x的取值有關嗎？

生9：無關，x是任意的。

教師安排學生活動，小組合作畫一些周期函數的圖像。

師：你們各小組能否檢查自己畫的這些圖像是否是周期函數的圖像呢？

生10：用定義檢驗。

師：很好，下面就請你們試著把周期函數的定義概括出來。

設計意圖：讓學生體會從特殊到一般的過程，三角函數也是一類特殊函數，體會周期函數的定義域的要求。通過小組合作，讓學生用數形結合更形象地去概括理解周期函數的概念。

問題五：將上述函數抽象成一般的函數，你能得到什么等式？

師：f（x+C）=f（x），現在請哪位同學試著給出周期函數的定義。

生11：函數f（x），對于任意的x，如果有f（x+C）=f（x），那么函數就叫作周期函數。

師：C是什么？

生11：常數，非零常數。

師：很好，請組織好語言，更好地定義一下周期函數的概念。

生11：一般的，對于函數f（x），如果存在一個非零常數C，使任意的x，都滿足f（x+C）=f（x），那么函數就叫作周期函數。

師：任意的x是整個實數集上嗎？

生12：應該是定義域內。老師，那周期函數的定義域是不是一定是整個實數集呢？

生13：可以不是整個實數集，比如可以只是整數集，f（x+1）=f（x），也可以是周期函數。

師：很好，那你再完善一下周期函數的定義。

生13：對于函數y=f（x），如果存在一個不為零的常數T，使當x取定義域內的每一個值時，f（x+C）=f（x）都成立，那么就把函數y=f（x）叫作周期函數。

設計意圖：總結出周期函數的定義，實現了從特殊到一般的建構。高度概括、表達準確且結論具備一般性。

問題7：若函數f（x）是一個周期函數，C為該函數的一個周期，該函數還有其他周期嗎？

生10：2π、-2π、4π、6π等等。

師：很好，你注意到負數也可以，而你這個總結的是三角函數的，一般函數呢？

生11：C、-C、2C、3C、kC等都是。

師：不錯，那也就說明周期函數的周期有無數多個，我們最好引入一個最具有代表性的周期，以更方便地描述周期函數的周期。

生12：C。

師：如何命名呢？

學生小聲討論：最小周期？不對，最小還可以是負的，正的最小周期？

師：很好，最小正周期。下面定義一下最小正周期。如果在所有正周期中有一個最小的，則稱它是函數f（x）的最小正周期。大家發現如果一個周期函數y=f（x）的所有周期中存在一個最小的正數，那么這個最小正數就叫作f（x）的最小正周期。

設計意圖：完善周期函數的定義，體會最小正周期引入的必要性，總結出最小正周期的定義。

（二）教學環節2：例題分析

例題：已知函數f（x）是一個周期函數，周期為2，并且f（x）=x2（x∈[0，2）），那么你能否畫出整個定義域上的圖像？

師：對于這個問題，你想從什么角度切入？

生13：我們只要畫出f（x）=x2（x∈[0，2））的圖像，那么其余地方的圖像都是和這個圖像一樣的。

生14：更準確地說應該先畫出f（x）=x2（x∈[0，2））的圖像，其余地方的圖像都是由這個圖像平移得到的，應該是左右平移得到的。

師：很好，那為什么是左右平移得到的呢？

生14：因為函數f（x）是一個周期函數，周期為2，也就是f（x+2）=f（x）。

師：不錯，我們發現對于周期函數，如果能畫出一個周期的圖像，那么通過周期函數的定義，就可以畫出整個函數的圖像。同理，如果知道一個周期的解析式，就可以根據定義寫出整個定義域的解析式。

教學反思：數學學科核心素養的落實，應該重點關注教學內容與教學結構的環節設計，由外到內逐步深入，合情合理地提出教學問題，以符合學生思維形成過程。對于“三角函數的周期性”的相關學習內容，會涉及以下問題：三角函數為什么會有周期性？三角函數的周期是多少？如何描述一般函數的周期性？教師通過上述三個問題逐步開展教學，可以促進學生形成學習數學的思想和方法，從“科學探究與創新意識”到“科學態度與社會責任”進一步揭示數學學習更高層次的價值追求。

數學概念的教學是培養學生核心素養的重要組成部分，合理設計概念的探究生成過程，是開展教學、落實核心素養教學的基本著力點。教師要創設合理的、實際的問題情境，提出具有開放性、挑戰性的問題，以概念的生成發展過程為主線，合理設計教學流程，將數學核心素養與整個教學過程融會貫通，促使學生在主動建構知識體系的過程中實現思維的發展。另外，在教育教學的過程中，要注重在課堂上互相滲透各類數學思想方法，使學生的學習由“散珠”的基本概念形成“串珠”的核心概念。

參考文獻：

[1]陸春霞. 追求自然而有深度的數學概念教學[J]. 中學數學研究，2022（09）：1-2.

[2]陳唐明. 和數學教師談如何有效研讀教材[J]. 中學數學教學參考，2016（13）：60-62.

[3]陳唐明. 本質的角度·思想的高度·思維的效度——高效數學課堂的三個基本維度[J]. 數學教學研究，2014，33（05）：2-4+14.

[4]劉長明. 基于核心素養的“三角函數”教材設計與教學思考[J]. 中學數學教學參考，2020（Z1）：50-53.

（責任編輯：淳? 潔）