讓轉化思想在數學課堂中落地生根

楊麗娟

摘 要：文章以專題“圓中角的轉化”的課堂教學為例，說明如何在數學課堂教學中滲透轉化思想——巧設情境，增強轉化的意識；知識回顧，尋找轉化的中介；解決問題，獲得轉化的方法。以此使學生理解轉化的作用，領會數學思想的重要性。

關鍵詞：數學思想；轉化意識；轉化中介；轉化方法

美國教育心理學家布魯納指出：掌握基本的數學思想，能使數學更易于理解和記憶。數學思想是數學的靈魂和精髓，領會科學的數學思想對提升思維品質、促進終身學習具有十分重要的意義［1］。

轉化也稱化歸，是一種常用的數學思想，是在研究和解決有關數學問題時采用某種手段將問題進行變換、轉化，進而解決問題的一種思維策略。其實質就是在已有知識的基礎上，利用各種變換解決問題。在教學中，教師可適當地挖掘教學內容中蘊含的轉化思想，并逐步實現滲透和應用。本文以數學專題“圓中角的轉化”的課堂教學為例，說明如何從增強轉化意識、尋找轉化中介、獲得轉化方法三方面著手，幫助學生理解轉化思想。

一、巧設情境，增強轉化意識

圓是重要的基本圖形，在長期的探索與研究中，人們發現了許多圓的相關性質。同時，角是圖形的重要元素，很多較為復雜的圖形都涉及角。圓錐曲線是初中階段的難點知識，學生在初次接觸時容易感到困難。而圓的特征賦予角極強的活性，如果將圓中的角進行靈活轉化，許多難題便能迎刃而解。教師可以在教學中創設有趣的問題情境，讓學生在解決問題的過程中感受轉化思想、增強轉化意識。

情境引入：

如圖1，在“世界杯”足球預選賽中，甲帶球向對方球門PQ進攻。當他帶球沖到A點時，同伴乙已經助攻沖到B點。現有兩種射門方式：第一種，甲直接射門；第二種，甲將球傳給乙，由乙射門。僅從射門角度考慮，應選擇哪種射門方式？為什么？

分析：僅從射門角度考慮射門方式即比較∠A與∠B的大小。連接PD，根據同弧所對的圓周角相等，發現∠PDQ=∠B，而∠PDQ是△PAD的外角，∠PDQ＞∠A，于是∠B＞∠A。因此，由乙在點B處射門有利。

如果連接QC，同樣可以得出答案。

設計意圖：添加輔助線，就是利用同弧所對的圓周角相等，將∠B轉化到∠PDQ，從而實現∠A與∠B的大小比較。這一問題情境可以讓學生意識到圓內角轉化的重要性，產生探究轉化思想的內需。

二、知識回顧，尋找轉化中介

中介是指在不同事物或同一事物內部對立兩極之間起居間聯系作用的部分。要進行圓中角的轉化，就要尋找轉化的中介。

例：如圖2-1，點A、B、C在⊙O上。

問題1：你找到了哪些與⊙O有關的角？這些角之間有怎樣的數量關系？

分析：利用圓心角的度數與它所對的弧的度數相等，得∠BOC=100°，利用圓周角的度數等于它所對的弧上圓心角度數的一半，得∠BAC=50°；利用等邊對等角，由半徑OB=OC，得∠OBC=∠OCB=40°。由此獲得轉化中介——半徑，實現邊角轉化。

分析：利用同弧或等弧所對的圓周角相等，由∠BAC=50°得∠BDC=50°。由此強調轉化中介——弧，說明位置變化，數量關系不變。

分析：利用圓內接四邊形的對角互補，由∠BAC= 50°，得∠BEC=130°，進而得∠BEF =50°，因此∠BEF=∠BAC，說明圓內接四邊形的外角等于它的內對角。由此獲得轉化中介——圓的內接四邊形，實現圓外角與圓內角的轉化。

分析：利用切線的性質，得∠OCG=∠OCH= 90°；利用余角的性質，由∠OCB=40°得∠BCH= 50°，因此∠BCH=∠BAC。由此獲得轉化中介——切線，實現弦切角與圓內角的轉化。

設計意圖：以一道操作題引出問題串，使圖形由淺入深。在保證學生思維連貫的前提下，通過動手動腦，既對圓中角的相關知識進行了回顧，又探索獲得了圓中角轉化的中介，為利用轉化思想解決數學問題做好鋪墊。

三、解決問題，獲得轉化方法

轉化的方法靈活多樣，既與實際問題的內容和特點有關，也與學生的認知結構有關。對于圓中角的轉化，在解決問題的過程中通過體驗獲得方法，不僅可以豐富經驗積累，還能提升數學素養。

（一）通過熱身練習，直接發現，應用轉化

教師可以設計一組簡單練習，直接利用轉化中介解決問題，使學生加深對轉化中介的掌握，鞏固對圓中角的轉化的理解及應用。學生經歷思考、交流，認知會更深刻。

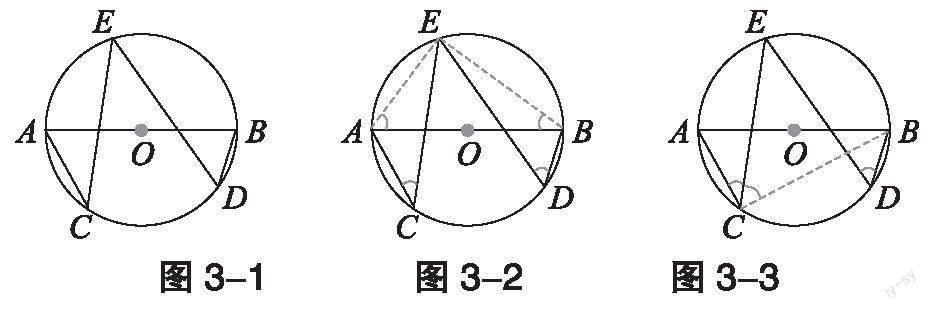
練習1：如圖3-1，AB是⊙O的直徑，C、D、E都是⊙O上的點，則∠C+∠D= 。

方法1——由弧看角

方法2——由角看弧

設計意圖：由弧看角，直接進行圓周角之間的等量轉化，學生容易想到。由角看弧，將圓周角轉化到圓弧上，實現抽象到直觀的轉變，非常簡潔。

練習2：已知四邊形ABCD是⊙O的內接四邊形，若∠A∶∠B∶∠C=4∶3∶5，則∠D的度數是（ ）

A.60° B.80° C.100° D.120°

設計意圖：利用圓的內接四邊形對角互補，求∠D的度數，直接轉化到∠B。由已知條件可知∠A=80°，∠B=60°，∠C=100°，因此∠D=120°。

練習3：如圖4，四邊形ABCD是⊙O的內接四邊形，AD與BC的延長線交于點E，BA與CD的延長線交于點F，若∠DCE=80°，∠F=25°，那么∠EDC的度數為 。

方法1：由已知條件∠DCE=80°，∠F=25°，可知∠B=55°，利用圓的內接四邊形的外角等于它的內對角，則∠EDC=∠B=55°。

方法2：利用圓的內接四邊形的外角等于它的內對角，由∠DCE=80°，知∠DAB=∠DCE=80°，于是∠FDA=55°，因此∠FDA的對頂角∠EDC=55°。

設計意圖：兩種方法都利用“圓的內接四邊形的外角等于它的內對角”的性質，將圓外角轉化為圓內角來解決問題。方法1綜合考慮兩個已知條件，思路相對簡潔。

（二）借助難點突破，添線構造，獲得轉化

可以設計有難度的練習，引導學生利用圓中角的轉化方法進行添線，構造轉化中介。學生經歷實踐探索，對獲得的數學經驗進行反思，能夠掌握解題策略，有效突破教學重難點。

A.120° B.130° C.140° D.150°

分析：如圖5-2，連接AC，利用直徑BC構造直角∠BAC。在Rt△ABC中，由三角函數可知∠B=30°，于是得到∠D=150°。

設計意圖：利用直徑構造直角，借助直角三角形實現邊角轉化。

練習5：如圖6-1，PA是⊙O的切線，切點為A，PO的延長線交⊙O于點B，連接AB。若∠P=40°，則∠B的度數為（ ）

A.20° B.25° C.40° D.50°

分析：如圖6-2，連接OA，利用切線PA構造直角∠PAO。在Rt△PAO中，由∠P=40°得到∠POA=50°，從而求得∠B=25°。

設計意圖：利用切線構造直角，借助直角三角形的兩個銳角互余，實現圓中角的轉化。

練習6：如圖7-1，已知AB是⊙O的直徑，C為⊙O上一點，CD⊥AB于點D，E是OB上一點，CE、AG交于點F。求證△ACG∽△AFC。

分析：題目已經滿足一對公共角相等的條件，即∠CAG=∠FAC。因為已知條件不涉及兩三角形的邊長，所以考慮借助圓中角的轉化，再求證一對角相等，從而證得兩三角形相似。

方法1：利用同弧，構造等角。如圖7-2，連接BC，得∠B=∠F；由直徑AB知∠ACB=90°。∵CD⊥AB，∴∠ADC=90°。由同角的余角相等，得到∠B=∠ACD，因而∠F=∠ACD，證得結論。

設計意圖：方法2通過添加輔助線，構造垂徑定理基本圖形，由垂徑定理得到等弧。由等弧得到等角，進行圓中角的轉化，有利于學生將陌生圖形轉變為自己熟悉的圖形。

練習7：如圖8-1，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，則∠CAD的度數為（ ）

A.68° B.88° C.90° D.112°

設計意圖：有些圖形問題雖然從表面上看與圓無關，但若能發現其中共圓的點、隱含的圓，就能運用圓中角的轉化解決問題，讓問題實現從復雜到簡單、從隱性到顯性的轉變。

結語

文中以圓中角的轉化為例，讓學生掌握如何應用轉化思想解決問題，感受轉化的作用，即化抽象為直觀、化生疏為熟悉、化復雜為簡單、化隱性為顯性，進而領會數學思想，提升數學素養。

［參考文獻］

王永春.小學數學與數學思想方法［M］.上海：華東師范大學出版社，2014.