結(jié)構(gòu)化教學，推動學習“自能化”

蘇丹

［摘 要］數(shù)學學習的本質(zhì)是將數(shù)學知識結(jié)構(gòu)轉(zhuǎn)變?yōu)樽陨碚J知結(jié)構(gòu)的過程。為了更好實現(xiàn)這個轉(zhuǎn)化，教師需要對課程內(nèi)容進行結(jié)構(gòu)化設(shè)計，梳理主題和脈絡(luò)，讓學習化繁為簡，真正實現(xiàn)學習“自能化”。文章以“梯形的面積計算”一課為例，闡述如何從教學目標的整體性、知識之間的關(guān)聯(lián)性、思想方法的一致性、練習設(shè)計的系統(tǒng)性四個方面進行結(jié)構(gòu)化教學。

［關(guān)鍵詞］梯形；結(jié)構(gòu)化；學習“自能化”

［中圖分類號］ G623.5 ［文獻標識碼］ A ［文章編號］ 1007-9068（2023）26-0069-03

數(shù)學來自人類勞動和探索客觀世界的具體實踐，從古人結(jié)繩計數(shù)到質(zhì)能方程，數(shù)學知識是從具體實踐中抽象而來的，具有結(jié)構(gòu)化屬性。數(shù)學學習的本質(zhì)是讓數(shù)學知識結(jié)構(gòu)與認知結(jié)構(gòu)相互作用，將數(shù)學知識結(jié)構(gòu)轉(zhuǎn)化為自身認知結(jié)構(gòu)的過程。

學生建立怎樣的認知結(jié)構(gòu)，取決于教師為他們提供怎樣的信息與知識。因此，教師首先要考慮課程內(nèi)容的結(jié)構(gòu)化設(shè)計。

從“結(jié)構(gòu)”的角度來展開教學，既能幫助學生建立數(shù)學知識間的邏輯聯(lián)系，又能幫助學生把握內(nèi)容的實質(zhì)。有個成語叫一葉知秋，因為有了結(jié)構(gòu)化的知識體系，所以可以從局部擴展到整體，如“一葉知秋”一般，從一片樹葉知道季節(jié)的交替，透過現(xiàn)象看本質(zhì)。結(jié)構(gòu)化教學正是希望培養(yǎng)學生的結(jié)構(gòu)化認知能力，使學生實現(xiàn)知識、方法的自主生長，從而擁有“一葉知秋”的能力。下面以“梯形的面積計算”一課為例，談談如何進行結(jié)構(gòu)化教學。

一、把握教學目標的整體性

結(jié)構(gòu)化教學是要學生通過回顧聯(lián)想、類比提升、反思積累，逐步將知識結(jié)構(gòu)內(nèi)化，培養(yǎng)學生對知識結(jié)構(gòu)的整體感知。這需要教師在組織結(jié)構(gòu)化學習時，整體把握課時內(nèi)容的教學價值，厘清某個領(lǐng)域知識的基本結(jié)構(gòu)，結(jié)合版塊整體目標，制訂合理、有效的課時目標。

多邊形面積計算教學有相同的模式，都是讓學生在觀察、操作、比較、推理等活動中探索平面圖形面積的計算方法。整個過程都圍繞“轉(zhuǎn)化”這一核心思想展開，在探究平行四邊形的面積時，學生初次嘗試運用切割、平移等方法進行圖形的轉(zhuǎn)化，初步感受轉(zhuǎn)化思想。緊接著探索三角形的面積公式時，學生學會運用轉(zhuǎn)化思想來計算三角形的面積，體驗轉(zhuǎn)化的意義。在探索梯形面積公式時，有了前兩節(jié)課的學習經(jīng)驗，學生自主遷移學習方法，也就實現(xiàn)了學習“自能化”。

另外，還可以對平面圖形面積的計算方法進行結(jié)構(gòu)化，雙向溝通平面圖形之間的聯(lián)系：把梯形轉(zhuǎn)化成其他平面圖形，再推導出梯形的面積公式；梯形的面積公式也服務于其他平面圖形，可用來計算其他平面圖形的面積。學生在感知知識整體性和結(jié)構(gòu)化的同時，體會數(shù)學抽象、邏輯推理、數(shù)學建模等思想方法，自主獲得探究同一類知識的學習路徑，培養(yǎng)核心素養(yǎng)。

教學“梯形的面積計算”一課時，筆者設(shè)計了以下教學目標。

1.在操作、觀察的過程中自主探究梯形的面積公式，培養(yǎng)自主學習的意識，發(fā)展空間觀念，提升學科素養(yǎng)。

2.在比較、分析、推理等數(shù)學活動中建立梯形的面積公式模型，并能利用公式解決生活中的實際問題，體會轉(zhuǎn)化的意義和價值，發(fā)展邏輯思維。

3.溝通梯形與其他平面圖形面積公式之間的聯(lián)系，感受數(shù)學知識的結(jié)構(gòu)美。

二、挖掘知識之間的關(guān)聯(lián)性

數(shù)學中的每一個知識點不是單獨存在的，都屬于某一個知識體系，考慮到學生的認知規(guī)律及其他因素，教材編排時切斷了一些知識鏈，使知識點猶如“散落的珍珠”分散在不同的學段里。因此，教師需要溝通知識間的內(nèi)在聯(lián)系，將分散的知識點串成知識鏈，編織成知識層級，再將知識層級建構(gòu)成知識結(jié)構(gòu)，從元素到系統(tǒng)，從局部到整體，讓學生從全局看清知識結(jié)構(gòu)體系的全貌，形成“從結(jié)構(gòu)的角度把握事物本質(zhì)”的結(jié)構(gòu)化思維。

[片段1]

師：同學們，前兩節(jié)課我們一起研究了平行四邊形、三角形的面積計算方法，我們是怎樣探索的？

生1：把平行四邊形分割、平移，轉(zhuǎn)化成長方形，轉(zhuǎn)化前后圖形的面積不變。

生2：把兩個完全相同的三角形拼成一個平行四邊形，可以發(fā)現(xiàn)其中一個三角形的面積是平行四邊形面積的一半。

師：探索平行四邊形、三角形面積公式的過程，有什么相同之處？

生3：都把新知轉(zhuǎn)化成了舊知。

師（出示圖1）：是的，轉(zhuǎn)化是數(shù)學學習中非常重要的數(shù)學思想。那么，你打算把梯形轉(zhuǎn)化成什么圖形，再求它的面積？試著用分割、添補、平移、旋轉(zhuǎn)等方法，把梯形轉(zhuǎn)化成已學過的平面圖形吧。

梯形的面積與前兩節(jié)課（平行四邊形的面積、三角形的面積）內(nèi)容相近、結(jié)構(gòu)相同，都可以通過割補、添補、平移、旋轉(zhuǎn)等方式把未知轉(zhuǎn)化成已知，從而探索面積計算方法。課堂上教師通過復習、回顧激發(fā)學生的已有經(jīng)驗，借助思維導圖溝通各平面圖形之間的聯(lián)系，以“你打算把梯形轉(zhuǎn)化成什么圖形？”為主線，利用新舊知識之間的共通性，引導學生展開遷移性學習，使知識具有自主生長的活力。

三、緊扣思想方法的一致性

數(shù)學學習的精髓不只在于習得幾個公式、記住幾個定律，更重要的是形成數(shù)學思想方法。成熟的數(shù)學思想方法是通向解決問題的橋梁，連接已知和未知，溝通理論與實踐。教師要善于將數(shù)學思想方法以及本質(zhì)規(guī)律進行有效遷移，將其延伸或者拓展到相似問題的解決過程中，形成新的解題思路，從而得到新的數(shù)學感悟和體會，建構(gòu)新的知識結(jié)構(gòu)化。

[片段2]

師：運用轉(zhuǎn)化思想，你把梯形轉(zhuǎn)化成了什么圖形？轉(zhuǎn)化前后的圖形面積有怎樣的關(guān)系？你還有什么發(fā)現(xiàn)？怎樣求梯形的面積？

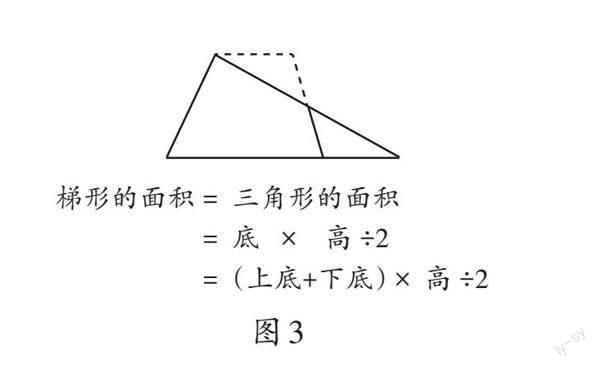
學生自主探究后匯報交流（如圖2、圖3）：

師：比較同學們的探究過程，有什么相同和不同的地方？

生1：得到的梯形面積公式相同。

生2：都運用了轉(zhuǎn)化的策略。

生3：公式中都有“[÷]2”。

師：同學們觀察得真仔細，用添補法（如圖2），梯形面積是平行四邊形的一半，因此梯形的面積公式中有“[÷]2”。為什么用分割法時（如圖3）也要“[÷]2”呢？

生4：計算圖3中三角形的面積時就要“[÷]2”。

師：是呀，不同的方法，“[÷]2”表示的意義也不同，但最終都成功把梯形轉(zhuǎn)化成了已學過的平面圖形，并得到了相同的梯形面積公式。

“多邊形面積”的教學重點在于讓學生感悟轉(zhuǎn)化思想，思想是一致的，但轉(zhuǎn)化方法有所不同。課堂上學生通過添補、分割等不同方法，把梯形轉(zhuǎn)化成了已學過的平面圖形，積累了豐富的活動經(jīng)驗，感受了轉(zhuǎn)化方法的多樣性，再次溝通了梯形與其他平面圖形之間的聯(lián)系。轉(zhuǎn)化后，教師通過“為什么要‘÷2’？”這一問題滲透“倍積變形”“等積變形”的數(shù)學思想，激發(fā)學生透過現(xiàn)象挖掘本質(zhì)，通過推理對比發(fā)現(xiàn)用不同的方法推導公式時，“[÷]2”的意義是不一樣的，使學生進一步感悟“雖然轉(zhuǎn)化方法不同，但結(jié)果相同”。整個過程中，教師給學生提供了充分的探索空間，有效提升了學生思維的靈活性，促進學生的思維邁向高階。

四、聚焦練習設(shè)計的系統(tǒng)性

有層次的練習能在鞏固本節(jié)課所學知識的同時，厘清知識之間的聯(lián)系，在“變”與“不變”中凸顯不同面積公式中相同的原理，將分散的知識用結(jié)構(gòu)化的思維穿成一條條線，結(jié)成一張張網(wǎng)，真正有效地促進學生對知識的掌握和理解。

生1：一樣大。

師：為什么？把你的想法和大家分享一下。

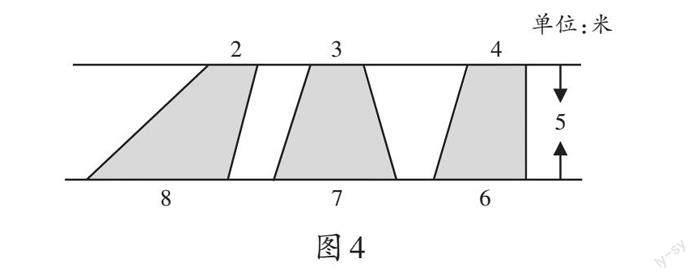
生1：因為三個梯形上底與下底的和都等于10，它們的高又是相等的，所以面積也相等。

師：這三個梯形雖然形狀不同，但它們上底加下底的和相等，高也相等，我們說這三個梯形是等底等高的。等底等高的情況下，它們的面積也相等。你還能說出一些與這三個梯形的高相等、面積也相等的圖形嗎？

生2：上底是1米，下底是9米，高是5米的梯形。

生3：底是5米，高是5米的平行四邊形。

生4：底是10米，高是5米的三角形。

師：同學們找到了這么多圖形，它們的面積都相等嗎？我們通過計算驗證一下。（學生口答驗證）

師：為什么平行四邊形、三角形的面積也可以用梯形的面積公式來計算呢？看了接下來的動畫你就能明白啦。

動畫演示：梯形的上底變大，當a=b（a是上底，b是下底）時，梯形就變成了平行四邊形，其面積公式可寫為S平行四邊形=（a+b）×h÷2=（a+a）×h÷2=2a×h÷2=a×h。

動畫演示：梯形的上底變小，當a=0時，梯形就變成了三角形，其面積公式可寫為S三角形=（a+b）×h÷2=（0+b）×h÷2=b×h÷2。

課堂上教師精心設(shè)計了三個形狀不同但面積相等的梯形，通過數(shù)形結(jié)合幫助學生明確：在高相等的情況下，只要“上底與下底的和”相等，那么這些梯形的面積也相等。以此為基礎(chǔ)，對于問題“你還能說出一些與這三個梯形的高相等、面積也相等的圖形嗎？”，學生能想到的就是高不變，上底與下底的和是10米的圖形。

這一環(huán)節(jié)的設(shè)計在更高層面上將三種圖形之間的聯(lián)系進行了溝通，提煉出共同的本質(zhì)以提升學生的遷移能力，并通過運動變化展示圖形的轉(zhuǎn)化過程。通過推理溝通三種圖形的面積公式，凸顯它們之間的內(nèi)在關(guān)聯(lián)，推導出可以相互轉(zhuǎn)化的多邊形的面積公式。這就是知識的結(jié)構(gòu)化，具有內(nèi)聯(lián)溝通、舉一反三、融會貫通的價值。

結(jié)構(gòu)化教學向?qū)W生展示了知識之間是有聯(lián)系的，是有機的整體，有先后邏輯，有主次關(guān)系，學生看到了整個結(jié)構(gòu)和生長的過程，才能理解數(shù)學從具體到抽象的演變，了解其內(nèi)在邏輯與意義。有了教學目標、內(nèi)容、思想方法、練習的結(jié)構(gòu)化設(shè)計，學生的學習方法、思維能力都向著結(jié)構(gòu)化的方向發(fā)展和完善，才能實現(xiàn)真正的學習“自能化”，從而推動數(shù)學素養(yǎng)自主生長。

［ 參 考 文 獻 ］

[1] 許衛(wèi)兵.小學數(shù)學整體建構(gòu)教學[M].上海：上海教育出版社，2022：73-102.

[2] 李雪梅.結(jié)構(gòu)化建構(gòu)概念 ? 系統(tǒng)化發(fā)展學生思維：以“認識負數(shù)”教學為例[J].教育科學論壇，2021（10）：57-60.

[3] 朱俊華.小學數(shù)學單元整體教學重在結(jié)構(gòu)關(guān)聯(lián)[J].中小學教師培訓，2021（4）：56-60.

（責編 黃 露）