高中數(shù)學(xué)中數(shù)形結(jié)合方法的應(yīng)用探討

朱天云

【摘要】數(shù)形結(jié)合是數(shù)學(xué)學(xué)習(xí)中一種應(yīng)用廣泛、效果顯著的數(shù)學(xué)思想，能夠促進學(xué)生對相關(guān)知識的深入理解，可以顯著提高學(xué)生的數(shù)學(xué)興趣，促使其能夠主動進行相關(guān)知識的探究.在新高考背景下，數(shù)形結(jié)合思想在高中數(shù)學(xué)教學(xué)中的應(yīng)用變得更加重要，這種數(shù)學(xué)思想強調(diào)的是學(xué)生對知識本質(zhì)的理解，符合新時代課程改革理念.為了使數(shù)形結(jié)合方法能夠得到良好的應(yīng)用，文章從數(shù)形結(jié)合方法的內(nèi)涵、應(yīng)用意義、應(yīng)用原則、應(yīng)用現(xiàn)狀以及應(yīng)用策略上展開具體論述，以供參考.

【關(guān)鍵詞】高中數(shù)學(xué)；數(shù)形結(jié)合；應(yīng)用探討

引 言

隨著新課改的不斷深入，傳統(tǒng)的高中數(shù)學(xué)教學(xué)模式已經(jīng)不能滿足學(xué)生的思維發(fā)展需要，教師必須采取有效的措施進行教學(xué)模式的創(chuàng)新，對只關(guān)注教材中理論知識灌輸?shù)慕虒W(xué)模式進行優(yōu)化，注重對學(xué)生進行思維的訓(xùn)練，確保學(xué)生能夠掌握知識的本質(zhì)，從而實現(xiàn)知識的遷移與運用.但是從目前教師應(yīng)用數(shù)形結(jié)合方法進行教學(xué)的現(xiàn)狀來看，還存在教學(xué)內(nèi)容陳舊、課堂互動少以及課后訓(xùn)練不足等問題，影響了數(shù)形結(jié)合方法作用的發(fā)揮.因此，相關(guān)教師需要深入反思，優(yōu)化教學(xué)，提升學(xué)生的學(xué)習(xí)效率.

一、數(shù)形結(jié)合方法概述

數(shù)形結(jié)合指的是通過分析問題中條件與結(jié)論的關(guān)聯(lián)，實現(xiàn)對代數(shù)意義的探究，同時展示出問題的幾何性質(zhì).在數(shù)學(xué)中，數(shù)量的描述具有精確、嚴謹?shù)奶攸c，而幾何圖形具有形象、直觀的特點，數(shù)形結(jié)合就是將二者進行融合，從而降低解題的難度，讓數(shù)學(xué)學(xué)習(xí)變得更加輕松.從高中數(shù)學(xué)的角度上進行分析，數(shù)形結(jié)合在高中階段具有重要地位.高中數(shù)學(xué)包含了大量的知識，并且具有一定難度，因此對學(xué)生的思維、能力等有著更高的要求，這就需要學(xué)生能夠掌握一定的數(shù)學(xué)思想，并且能夠進行有效的運用，以此來提高學(xué)習(xí)效果.因此，教師在進行高中數(shù)學(xué)教學(xué)時，應(yīng)該注重對數(shù)學(xué)結(jié)合方法的有效利用，幫助學(xué)生牢固掌握相關(guān)數(shù)學(xué)知識.

二、高中數(shù)學(xué)教學(xué)應(yīng)用數(shù)形結(jié)合方法的意義

（一）有利于提升課堂教學(xué)效果

數(shù)形結(jié)合方法的應(yīng)用，可以顯著降低解題難度，提高教學(xué)效果.學(xué)生在解決相關(guān)數(shù)學(xué)問題時，若是問題中僅僅提供了圖形或者數(shù)據(jù)，那么就需要學(xué)生結(jié)合自己的數(shù)學(xué)認知，進行題目的轉(zhuǎn)化，形成數(shù)據(jù)或者圖形，這是一種高效的解題思想.也就是說，教師應(yīng)該注重對學(xué)生數(shù)形結(jié)合思想的培養(yǎng)，讓學(xué)生能夠在看到數(shù)學(xué)語言時，大腦中形成對應(yīng)的圖形；在看到題目中的圖形信息時，能夠聯(lián)想到圖形對應(yīng)的數(shù)量關(guān)系，以此來促進學(xué)生高效解題，提高他們做題的準確率.因此，教師在高中數(shù)學(xué)教學(xué)中，重視數(shù)形結(jié)合方法的教學(xué)，可以在一定程度上強化教學(xué)效果.

（二）有利于增強學(xué)生的學(xué)習(xí)興趣

數(shù)形結(jié)合方法的核心是圖形和數(shù)量的融合，不僅可以讓問題變得更加直觀，還可以在一定程度上提高解題的趣味性，有助于學(xué)生數(shù)學(xué)興趣的提升，同時能夠促進學(xué)生形象思維的生成.相比于小學(xué)和初中數(shù)學(xué)，高中數(shù)學(xué)在難度上顯著提高，數(shù)學(xué)知識具有較強的抽象性、廣泛性以及邏輯性.數(shù)學(xué)知識深度和廣度的提高，讓很多學(xué)生難以適應(yīng)，不能理解相關(guān)知識的本質(zhì).久而久之，學(xué)生就會抵觸數(shù)學(xué)學(xué)習(xí)，漸漸地對數(shù)學(xué)失去興趣.而教師通過在教學(xué)中教授學(xué)生數(shù)形結(jié)合的方法，可以改善這種情況，能夠?qū)崿F(xiàn)對抽象知識的轉(zhuǎn)化，讓問題變得更加具象，促進學(xué)生深入理解相關(guān)知識的本質(zhì).

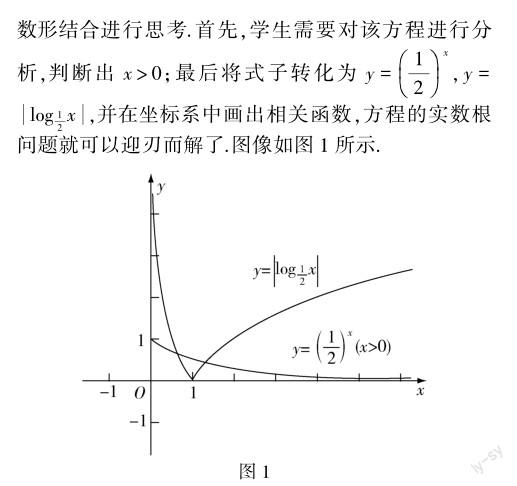
此時，學(xué)生可以根據(jù)圖像去分析方程的實數(shù)根，最終求得此題的結(jié)果，圖像有兩個交點，所以方程的實數(shù)根有2個.這樣大大降低了解題的難度，并且能夠顯著提升學(xué)生探究的興趣.

（三）有利于學(xué)生思維的發(fā)展

數(shù)形結(jié)合是由“數(shù)”和“形”組成的，二者是對立統(tǒng)一關(guān)系.在數(shù)學(xué)學(xué)習(xí)中，“數(shù)”和“形”不應(yīng)該獨立存在，只有有機結(jié)合，才可以有效轉(zhuǎn)化.這一過程中，學(xué)生的思維會得到訓(xùn)練，變得更加靈活，進而增強自身的學(xué)習(xí)能力.

例如，教師在教學(xué)“拋物線”相關(guān)知識時，可以通過數(shù)形結(jié)合的方式引導(dǎo)學(xué)生進行思考，使他們的思維得到訓(xùn)練.

例2 在拋物線y2=4x上有一點B，使得點B到y(tǒng)=x+3的距離最短.

該命題可轉(zhuǎn)化為求一條平行于y=x+3的直線，y=x+b與拋物線y2=4x相切，求出切點，此時點B到直線y=x+3的距離最短，然后將y=x+b與y2=4x聯(lián)立，可以求出B（1，2），使得點B到直線y=x+3的距離最短.圖像如圖2所示.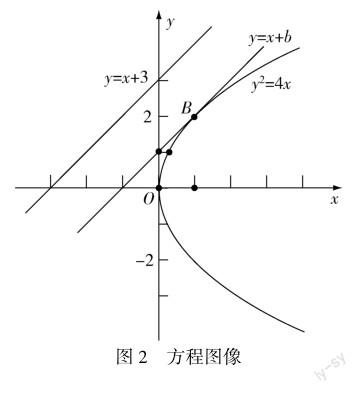

通過與圖形結(jié)合的方式，知識變得更加直觀，有助于學(xué)生思考，從而使學(xué)生正確解題.

三、高中數(shù)學(xué)教學(xué)應(yīng)用數(shù)形結(jié)合方法的原則

教師想要讓數(shù)形結(jié)合方法得到有效利用，那么在教學(xué)中應(yīng)該遵循雙向性原則.雙向性指的是在數(shù)形結(jié)合中，“數(shù)”可以向“形”轉(zhuǎn)化，同時“形”可以向“數(shù)”轉(zhuǎn)化.在教學(xué)的過程中，教師應(yīng)該結(jié)合問題實際，進行數(shù)形的轉(zhuǎn)化.從圖形上看，空間圖形能夠讓數(shù)的特征清晰展現(xiàn).而從代數(shù)上看，其主要特征是嚴謹精確，可以引導(dǎo)學(xué)生分析問題中的數(shù)量關(guān)系，還可以突破空間圖形的直觀約束，通過數(shù)更加深入地研究圖形.也就是說，學(xué)生在利用數(shù)形結(jié)合進行解題時，不應(yīng)該局限在數(shù)化形或者形化數(shù)上，應(yīng)該考慮到雙向性，將二者有機結(jié)合，才能夠?qū)崿F(xiàn)高效利用.

四、高中數(shù)學(xué)教學(xué)應(yīng)用數(shù)形結(jié)合方法的策略

（一）利用數(shù)形結(jié)合方法優(yōu)化教學(xué)內(nèi)容

在教育改革不斷深化的背景下，素質(zhì)教育變得越來越重要.以往“一言堂”的灌輸式教學(xué)已經(jīng)是過去式了.在新時代的高中數(shù)學(xué)教學(xué)中，教師應(yīng)該注重對學(xué)生思維的引導(dǎo)，促使學(xué)生能夠主動進行知識的探究、思考知識的內(nèi)涵和性質(zhì)等.只有這樣，才能提升學(xué)生的數(shù)學(xué)熱情，讓他們對抽象的數(shù)學(xué)形成長久的興趣.數(shù)形結(jié)合可以有效訓(xùn)練學(xué)生思維，促進其主動學(xué)習(xí).因此，教師在進行教學(xué)時，可以結(jié)合教材內(nèi)容，進行數(shù)形結(jié)合方法的教學(xué)，從而實現(xiàn)內(nèi)容的優(yōu)化，同時通過這種方式幫助學(xué)生深度理解教材中的知識，讓學(xué)生能夠輕松地學(xué)習(xí)數(shù)學(xué)，為更高階的知識學(xué)習(xí)打下基礎(chǔ).

教師應(yīng)該從學(xué)生升入高中就開始就培養(yǎng)他們的數(shù)形結(jié)合思想.在教學(xué)的過程中，教師應(yīng)該讓學(xué)生對教材中“數(shù)”和“形”的內(nèi)容進行區(qū)分，正確地對教材中數(shù)量和圖形的內(nèi)容進行分析，使學(xué)生可以利用數(shù)形結(jié)合的方法進行知識點的記憶以及題目的解決等等，讓學(xué)生在數(shù)學(xué)學(xué)習(xí)的過程中潛移默化地形成數(shù)形結(jié)合思想.

例如，教師在進行“集合與常用的邏輯用語”這一章教學(xué)時，就應(yīng)該深入分析教材，注重數(shù)形結(jié)合方法的滲透.如教師在講解集合的概念時，就可以引入圖形內(nèi)容.集合的概念中涉及全集、交集以及并集等相關(guān)知識.為促使學(xué)生能夠深入理解這些概念，教師可以帶領(lǐng)學(xué)生進行相關(guān)圖形的繪制，如圖3所示.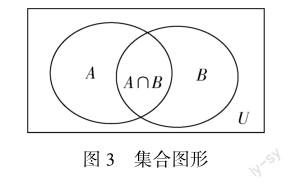

（二）利用數(shù)形結(jié)合方法提升學(xué)生的學(xué)習(xí)興趣

興趣是學(xué)生主動進行數(shù)學(xué)知識探究的動力.想要提高學(xué)生的學(xué)習(xí)效果，興趣的培養(yǎng)十分關(guān)鍵.但是，從目前高中生對待數(shù)學(xué)的實際態(tài)度來看，很多學(xué)生對數(shù)學(xué)的興趣并不高，特別是數(shù)學(xué)基礎(chǔ)一般的學(xué)生，他們甚至對數(shù)學(xué)有厭煩心理.對于這類學(xué)生而言，他們不敢去分析具有較強抽象性的題目.比如，函數(shù)的最值問題，有些學(xué)生一看到最值問題，直接選擇放棄.長期處于這樣的狀態(tài)下，學(xué)生的消極情緒就會逐漸累積，從而放棄學(xué)習(xí)數(shù)學(xué)，不再和教師進行互動，數(shù)學(xué)成績也會出現(xiàn)大幅度下滑.針對這種情況，教師可以通過數(shù)形結(jié)合的方法，創(chuàng)設(shè)相關(guān)的數(shù)學(xué)情境，幫助學(xué)生理解數(shù)和形的關(guān)系，讓他們通過回答教師的問題，產(chǎn)生學(xué)習(xí)數(shù)學(xué)的興趣.

（三）利用數(shù)形結(jié)合方法強化課后訓(xùn)練

數(shù)形結(jié)合對數(shù)學(xué)學(xué)習(xí)具有重要作用，可以促使學(xué)生數(shù)學(xué)能力的不斷提升.教師在利用數(shù)學(xué)結(jié)合方法進行教學(xué)時，應(yīng)該將其應(yīng)用到整個教學(xué)過程中，還應(yīng)該將其融入課后的強化訓(xùn)練中，讓學(xué)生能夠充分地接觸數(shù)形結(jié)合.課后訓(xùn)練是數(shù)學(xué)教學(xué)的重要組成，具有檢驗和鞏固數(shù)學(xué)知識的作用.教師要重視讓學(xué)生在課后訓(xùn)練中也能夠進行數(shù)形結(jié)合方法的練習(xí)，使學(xué)生能夠?qū)?shù)形結(jié)合思想內(nèi)化于心，以此來不斷提升學(xué)生的解題能力.下面以“不等式”題目教學(xué)為例.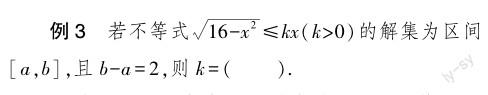

這道題通過正常求解十分復(fù)雜，通過圖像法可以清晰地展示出題目答案.同時，學(xué)生在畫圖的過程中，思維可以得到有效訓(xùn)練.根據(jù)此題，可以得到如圖4所示圖像.

結(jié) 語

綜上所述，數(shù)形結(jié)合是高中數(shù)學(xué)中重要的教學(xué)思想，可以促進教學(xué)效果的提升、學(xué)生興趣的增強以及學(xué)生思維的發(fā)展.因此，教師應(yīng)該注重數(shù)形結(jié)合方法的應(yīng)用，在教學(xué)中運用等價性、雙向性原則進行思想的滲透.同時，教師應(yīng)該認識到自己在數(shù)形結(jié)合教學(xué)中的不足，有針對性地進行改進.

【參考文獻】

[1]盧思聰.高中數(shù)學(xué)教學(xué)中數(shù)形結(jié)合方法的有效應(yīng)用[J].高考，2021（20）：24-25.

[2]陳建勤.高中數(shù)學(xué)教學(xué)中數(shù)形結(jié)合思想方法的應(yīng)用[J].考試周刊，2018（18）：69.

[3]牛菊霞.高中數(shù)學(xué)教學(xué)與解題中數(shù)形結(jié)合思想方法的應(yīng)用分析[J].考試周刊，2021（12）：75-76.

[4]田娟.高中數(shù)學(xué)教學(xué)中數(shù)形結(jié)合方法的有效應(yīng)用[J].數(shù)學(xué)學(xué)習(xí)與研究，2021（2）：25-26.

[5]王仁貴.淺析高中數(shù)學(xué)教學(xué)中數(shù)形結(jié)合方法的應(yīng)用[J].學(xué)苑教育，2019（18）：60-61.

[6]李曉明.高中數(shù)學(xué)教學(xué)與解題中數(shù)形結(jié)合思想方法的應(yīng)用分析[J].中國新通信，2018（7）：209.