創設逐層遞進的問題情境，發展學生的數學學科核心素養

黃雅倩

［摘? 要］ 科學、合理的問題情境能有效激活學生的思維，引發學生思考與交流，發展學生的數學學科核心素養. 研究者以“弧度制”為例，從“情境創設，復習導入”“活動探究，形成概念”“揭露本質，建立聯系”“應用新知，深化理解”“歸納總結，提煉升華”等方面展開教學，并從如下幾點談一些思考：注重滲透數學文化，激趣啟思；關注知識內在聯系，完善認知體系；加強提煉數學思想，發展素養.

［關鍵詞］ 問題情境；核心素養；弧度制

科學、合理的問題情境往往能有效激活學生的思維，培養學生學習的內驅力，引發學生思考與交流. 基于學生的最近發展區設計逐層遞進的問題情境，是踐行新課標要求的基礎，也是不斷拔高學生思維、提升學生數學學科核心素養的保障. 為了驗證這種說法，筆者對此進行了實踐與研究，現以“弧度制”的教學為例，展開實踐與思考.

教學分析

“弧度制”具有承上啟下的作用，“上”為初中階段所學的“度（角的度量單位）”，“下”為高中階段推廣的角的認識，學生在本節課前對“任意角”已有所了解. 本節課作為“三角函數”章節的第二課，教學初始目標在于引發學生認知矛盾，矛盾體現在“角度與三角函數值之間無法直接運算”方面，完成該目標，“弧度制”也應運而生. 關于“三角函數自變量與函數值的單位”問題的統一，可讓角與實數之間形成對應的聯系，這對后續研究任意角的三角函數以及函數相關運算等具有關鍵性的作用.

教學簡錄

1. 情境創設，復習導入

情境1 在正弦表的研究歷程中，印度數學家阿耶波多意外發現在等式sin30°=0.5中，等號右側的實數0.5與等號左側的sin30°的單位制不同. 顯然，這是一個矛盾. 在這種背景下，我們可否計算出sin30°+30°的具體值是多少？

設計意圖 課堂起始階段，將數學史料作為課堂導入的第一個情境，意在啟發學生思考，讓學生突破原本對問題封閉的認識，感知“角度”的正弦值實則為“實數”. sin30°+30°這個式子的提出，為學生思考指明了方向，即角度的正弦值與角度是否可以相加？sin30°為實數，而30°卻是角的度數，因此兩者并不具備相加的條件，由此成功引發了學生的認知沖突，為接下來的教學奠定了基礎.

問題1 你們接觸過哪些度量角的單位？

生1：初中階段接觸過度量角的單位有：度、分、秒.

師：這三個單位的進位制分別是什么？

生2：1度為60分，1分為60秒，因此為六十進制.

師：我們該如何定義1度的角呢？

生3：可將1度的角理解為周角的.

隨著交流的深入，不僅勾起了學生對角度制的回憶，還促使學生自主抽象出什么是角度制，為接下來更加深入的探索做鋪墊.

問題2 大家還記得之前的學習中，接觸過哪些單位制可用來度量長度嗎？它們各自的進位制是什么？

在這個問題的啟發下，學生快速搜索知識結構，很快就總結出常見的度量長度的單位制有米、碼、英尺等，而且這幾種單位制均屬于十進制.

師：既然度量長度的單位制有多種，那么度量角的單位制是否也存在多種呢？我們可否借助不同的單位制對角進行度量？能否應用十進制的實數來度量角的大?。?/p>

設計意圖 舊知的復習意在讓學生更清晰地理解度量角的單位制以及度量長度的單位制是什么，激發學生探索角度單位制的興趣，為弧度制的引入做鋪墊. 在類比思想的幫助下，學生初步感知知識間的聯系，這對提升學生的數學抽象能力、類比推理能力等具有重要影響.

2. 活動探究，形成概念

探究內容 用十進制的實數來度量角的大小，需以“任意角”的定義作為出發點，探索與角度大小相關的量.

如圖1所示，射線OA圍繞端點O旋轉至OB處形成角α. 在旋轉過程中，射線OA上的一點P（非端點）形成的軌跡為一個圓弧，這個圓弧與圓心角α呈相對應的關系.

問題3 說說圖1中射線OA在旋轉時涉及哪些條件，所涉及的條件之間有沒有什么關聯點？

學生略作思考，很快就給出明確的結論：射線OA在旋轉時涉及的條件有圓的半徑、弧長與圓心角等，這些條件之間存在一定的關聯性，如在半徑不發生改變的背景下，圓心角的度數越大，則圓心角所對應的弧長也越長.

設計意圖 調動學生已有的學習經驗與認知基礎，促使學生更好地建構與內化新知. 圓心角影響因素的研究順利勾起了學生已有的認知經驗，為抽象弧度制的概念奠定了基礎.

3. 揭露本質，建立聯系

師：正角、負角、零角受什么因素影響？

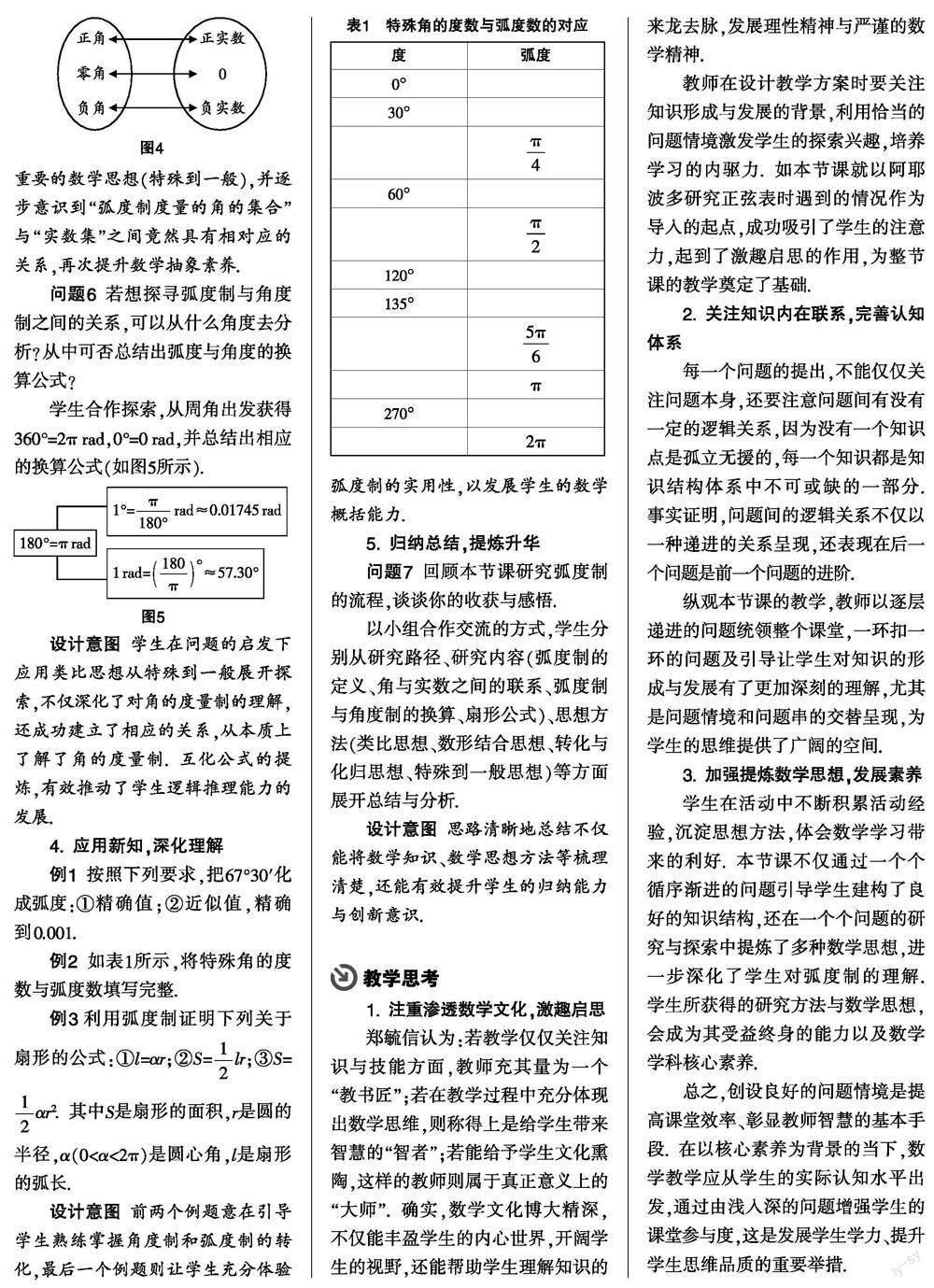
師：通過以上探索，大家覺得“弧度制度量的角的集合”與“實數集”之間有聯系嗎？

師生、生生積極互動，建立它們相對應的關系（如圖4所示）.

設計意圖 數學文化的滲透進一步激發學生對弧度制的研究興趣，并深化學生對弧度制的認識. 學生在此環節感知到弧度制的本質，感悟到重要的數學思想（特殊到一般），并逐步意識到“弧度制度量的角的集合”與“實數集”之間竟然具有相對應的關系，再次提升數學抽象素養.

問題6 若想探尋弧度制與角度制之間的關系，可以從什么角度去分析？從中可否總結出弧度與角度的換算公式？

學生合作探索，從周角出發獲得360°=2π rad，0°=0 rad，并總結出相應的換算公式（如圖5所示）.

設計意圖 學生在問題的啟發下應用類比思想從特殊到一般展開探索，不僅深化了對角的度量制的理解，還成功建立了相應的關系，從本質上了解了角的度量制. 互化公式的提煉，有效推動了學生邏輯推理能力的發展.

4. 應用新知，深化理解

例1 按照下列要求，把67°30′化成弧度：①精確值；②近似值，精確到0.001.

例2 如表1所示，將特殊角的度數與弧度數填寫完整.

設計意圖 前兩個例題意在引導學生熟練掌握角度制和弧度制的轉化，最后一個例題則讓學生充分體驗弧度制的實用性，以發展學生的數學概括能力.

5. 歸納總結，提煉升華

問題7 回顧本節課研究弧度制的流程，談談你的收獲與感悟.

以小組合作交流的方式，學生分別從研究路徑、研究內容（弧度制的定義、角與實數之間的聯系、弧度制與角度制的換算、扇形公式）、思想方法（類比思想、數形結合思想、轉化與化歸思想、特殊到一般思想）等方面展開總結與分析.

設計意圖 思路清晰地總結不僅能將數學知識、數學思想方法等梳理清楚，還能有效提升學生的歸納能力與創新意識.

教學思考

1. 注重滲透數學文化，激趣啟思

鄭毓信認為：若教學僅僅關注知識與技能方面，教師充其量為一個“教書匠”；若在教學過程中充分體現出數學思維，則稱得上是給學生帶來智慧的“智者”；若能給予學生文化熏陶，這樣的教師則屬于真正意義上的“大師”. 確實，數學文化博大精深，不僅能豐盈學生的內心世界，開闊學生的視野，還能幫助學生理解知識的來龍去脈，發展理性精神與嚴謹的數學精神.

教師在設計教學方案時要關注知識形成與發展的背景，利用恰當的問題情境激發學生的探索興趣，培養學習的內驅力. 如本節課就以阿耶波多研究正弦表時遇到的情況作為導入的起點，成功吸引了學生的注意力，起到了激趣啟思的作用，為整節課的教學奠定了基礎.

2. 關注知識內在聯系，完善認知體系

每一個問題的提出，不能僅僅關注問題本身，還要注意問題間有沒有一定的邏輯關系，因為沒有一個知識點是孤立無援的，每一個知識都是知識結構體系中不可或缺的一部分. 事實證明，問題間的邏輯關系不僅以一種遞進的關系呈現，還表現在后一個問題是前一個問題的進階.

縱觀本節課的教學，教師以逐層遞進的問題統領整個課堂，一環扣一環的問題及引導讓學生對知識的形成與發展有了更加深刻的理解，尤其是問題情境和問題串的交替呈現，為學生的思維提供了廣闊的空間.

3. 加強提煉數學思想，發展素養

學生在活動中不斷積累活動經驗，沉淀思想方法，體會數學學習帶來的利好. 本節課不僅通過一個個循序漸進的問題引導學生建構了良好的知識結構，還在一個個問題的研究與探索中提煉了多種數學思想，進一步深化了學生對弧度制的理解. 學生所獲得的研究方法與數學思想，會成為其受益終身的能力以及數學學科核心素養.

總之，創設良好的問題情境是提高課堂效率、彰顯教師智慧的基本手段. 在以核心素養為背景的當下，數學教學應從學生的實際認知水平出發，通過由淺入深的問題增強學生的課堂參與度，這是發展學生學力、提升學生思維品質的重要舉措.