多維探究課本例題 發(fā)展學生核心素養(yǎng)

摘 要：首先給出課本一道求軌跡方程例題的多種解法，然后根據(jù)例題給出的條件探究出更多的結(jié)論，并類比推廣到橢圓和雙曲線，給出了相應性質(zhì).結(jié)合課本例題，在核心素養(yǎng)導向下，運用“問題解決”教學模式，將核心素養(yǎng)融入課堂教學中.

關(guān)鍵詞：核心素養(yǎng)；軌跡方程；探究；最小值

中圖分類號：G632?? 文獻標識碼：A?? 文章編號：1008-0333（2024）07-0029-09

教材是重要的課程資源，這是毋庸置疑的.教材中

有的例習題具有拓展性，可以設計為具有科學探究價值的問題或課題，以此為載體，引導學生合理運用科學的思維方法，分析問題或進行深入研究.對于廣大學生提高核心認知品質(zhì)，發(fā)展關(guān)鍵能力，進而提升學科核心素養(yǎng)，具有深遠意義.

1? 課本例題，探究之源

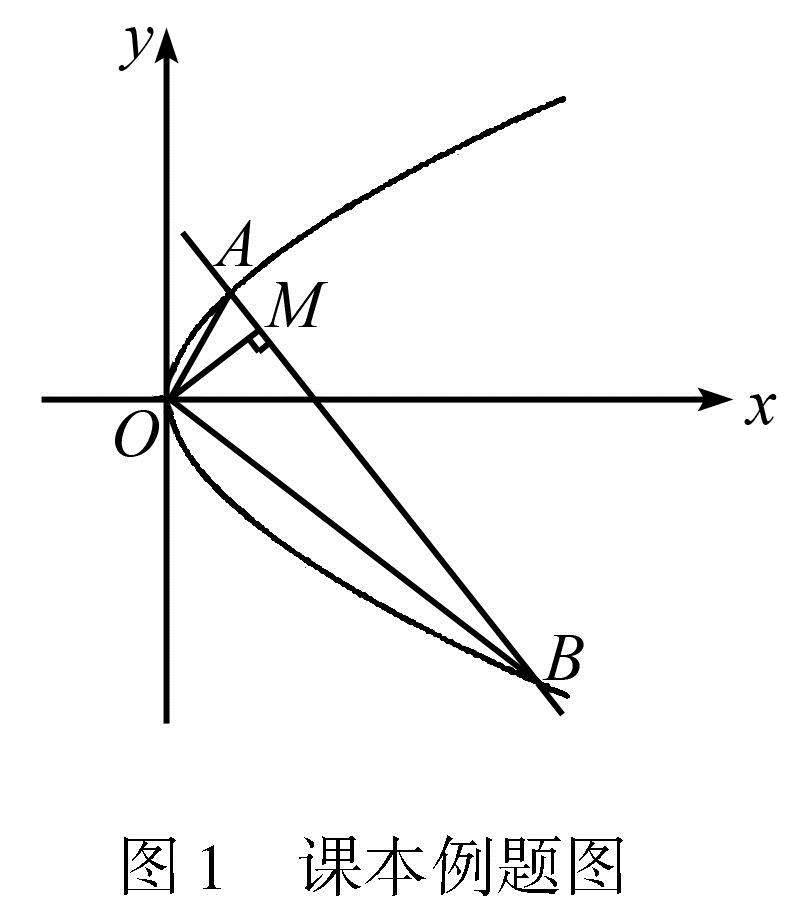
題目 如圖1，O是直角坐標原點，A，B是拋物線y2=2px（p>0）上異于頂點的兩動點，且OA⊥OB，OM⊥AB并與AB相交于點M，求點M的軌跡方程［1］.

此題是人教社A版（2007年1月第2版）普通高中課程標準實驗教科書數(shù)學選修4-4《坐標系與參數(shù)方程》第33頁例3.

2 解法探究，曲徑通幽

思路1 設A，B兩點坐標，分別寫出直線AB，OM方程，充分利用OA⊥OB這一條件，即可求出點M的軌跡方程.

即（y1+y2）y-2px-y1y2=0.

由OA⊥OB，有y1y2=-4p2.

故（y1+y2）y-2px+4p2=0.①

將②代入①整理，得

x2+y2-2px=0（x≠0）.

當y1+y2=0時，點M的坐標是（2p，0），此時點M的坐標滿足方程x2+y2-2px=0（x≠0）.

因此，點M的軌跡方程是x2+y2-2px=0（x≠0）.

思路2 利用kAB·kOM=-1建立等式，消去參數(shù)得軌跡方程.

y2-（y1+y2）y+（y1+y2）y0-2px0=0.

故 y1y2=（y1+y2）y0-2px0.

又y1y2=-4p2，

化簡，得x20+y20-2px0=0（x0≠0）.

當y1+y2=0時，點M的坐標是（2p，0），此時點M的坐標滿足方程x2+y2-2px=0（x≠0），

因此，點M的軌跡方程是x2+y2-2px=0（x≠0）.

思路3 充分挖掘已知條件，由已知我們易知直線與x軸交于定點N（2p，0），這樣一來，問題就好解決了.

解法3 設M（x，y），由解法1中的①式，即

（y1+y2）y-2px+4p2=0.

易得 （y1+y2）y-2p（x-2p）=0.

故直線AB過定點N（2p，0）.

即x2+y2-2px=0（x≠0）.

因此，點M的軌跡方程是x2+y2-2px=0（x≠0）.

思路4 建立直線AB的斜截式方程y=kx+b，然后y=kx+b與y2=2px聯(lián)立，并利用已知條件OA⊥OB，用p和b表示k，把k代入y=kx+b，也可以得到直線AB過定點N（2p，0）.

解法4 設直線AB的方程為y=kx+b（bk≠0），

k2x2+（2kb-2p）x+b2=0.

設A（x1y1），B（x2，y2），則

又由OA⊥OB，得x1x2+y1y2=0.

故直線AB過定點N（2p，0），下同解法3.

思路5 利用拋物線的參數(shù)方程，設A，B的坐標分別（2pt21，2pt1），（2pt22，2pt2）（t1≠t2且t1·t2≠0），然后利用平面向量有關(guān)知識來求解.

即（2pt1t2）2+（2p）2t1t2=0.

所以t1t2=-1.⑤

即2px（t22-t21）+2py（t2-t1）=0.

所以x（t1+t2）+y=0.

所以（x-2pt21）（2pt2-y）=（y-2pt1）（2pt22-x）.

化簡，得x-（t1+t2）y+2pt1t2=0.⑦

即x2+y2-2px=0（x≠0），這就是點M的軌跡方程.

設點M的坐標為（x，y），則

由A，B，M三點共線可得

由OM⊥AB，得kAB·kOM=-1.

當k≠±1時，點M的坐標是（2p，0），此時點M的坐標滿足方程x2+y2-2px=0（x≠0）.

即x2+y2-2px=0（x≠0），這就是點M的軌跡方程.

解法7 設點M，A，B的坐標分別為（x，y），（x1，y1），（x2，y2）.

又y21=2px1，y22=2px2，

所以x1x2=4p2，y1y2=-4p2.

又|y1-y2|≠0，即x2+y2-2px=0（x≠0），這就是點M的軌跡方程.

思路8 設點M，A，B的坐標分別為（x，y），（x1，y1），（x2，y2），求出AB的斜率，利用OM⊥AM，OM⊥BM，OM⊥AB，再由平面向量有關(guān)知識可求出點M的軌跡方程.

由OA⊥OB易得y1y2=-4p2.

把B12代入B13，得

即x2+y2-2px=0（x≠0），這就是點M的軌跡方程.

思路9 M是Rt△AMO與Rt△BMO的交點，也就是以OA為直徑的圓與以OB為直徑的圓的交點，這樣可以利用圓的直徑式方程求解.

化簡，得y1y2=-4p2.

以OA為直徑的圓的方程為

以OB為直徑的圓的方程為

由14-15，得

由14+15，得

把y1·y2=-4p2代入B17，得

把B16代入B18，化簡得x2+y2-2px=0（x≠0），這就是點M的軌跡方程.

思路10 利用極坐標求軌跡方程.在利用極坐標求曲線方程時，關(guān)鍵是找出曲線上的點滿足的幾何條件，將它用極坐標表示，再通過代數(shù)變換進行化簡.而且，與用平面直角坐標求曲線方程相比，求它的極坐標方程更加簡便，代數(shù)變換更加直接.根據(jù)題目的要求可以把極坐標方程化成直角坐標方程.

解法10 由求軌跡方程解法1中的①式知直線AB過定點N（2p，0）.

3 根植沃土，橫縱拓展

解答完例3之后，課本給出了“探究：在例3中，點A，B在什么位置時，△AOB的面積最小？最小值是多少？”這可以看成是例3的變式，教參給出的解答是解法1，在此給出“探究”的多種解法.

探究1 如圖1，O是直角坐標原點，A，B是拋物線y2=2px（p>0）上異于頂點的兩動點，且OA⊥OB，當點A，B在什么位置時，△AOB的面積最小？最小值是多少？

解法1 由例3（課本上例3）可得

當且僅當t1=-t2，即當點A，B關(guān)于x軸對稱時，△AOB的面積最小，最小值為4p2.

解法2 設A（x1，y1），B（x2，y2）.

由OA⊥OB，易知

x1x2+y1y2=0，x1x2=4p2，y1y2=-4p2.

當且僅當x1=x2且y1=-y2，即當點A，B關(guān)于x軸對稱時，△AOB的面積最小，最小值為4p2.

由OA⊥OB，易知

當且僅當x1=x2且y1=-y2，即當點A，B關(guān)于x軸對稱時，△AOB的面積最小，最小值為4p2.

當k=±1時上式等號成立，即當點A，B關(guān)于x軸對稱時，△AOB的面積最小，最小值為4p2.

解法5 由求軌跡方程解法3知直線AB過定點N（2p，0），

可設直線AB的方程為x-2p=ty，A（x1，y1），

B（x2，y2），

把B19代入B20，整理得

y2-2pty-4p2=0.

所以y1+y2=2pt，y1y2=-4p2.

當且僅當t=0時，上式等號成立.即當點A，B關(guān)于x軸對稱時，△AOB的面積最小，最小值為4p2.

解法6 把y2=2px化成極坐標方程

探究2 如圖1，O是直角坐標原點，A，B是拋物線y2=2px（p>0）上異于頂點的兩動點，且OA⊥OB，求|AB|的最小值.

x1x2=4p2，y1y2=-4p2.

當且僅當y1=-y2時等號成立，所以|AB|的最小值為4p.

解法2 由求軌跡方程解法3知直線AB過定點N（2p，0），可設直線AB的方程為x-2p=ty，A（x1，y1），B（x2，y2）.

把B19代入B20，整理得y2-2pty-4p2=0.

所以y1+y2=2pt，y1y2=-4p2.

當且僅當t=0時等號成立，所以|AB|的最小值為4p.

探究3 如圖1，O是直角坐標原點，A，B是拋物線y2=2px（p>0）上異于頂點的兩動點，且OA⊥OB，求|OA|+|OB|的最小值.

當且僅當y1=-y2時等號成立，

探究4 如圖1，O是直角坐標原點，A，B是拋物線y2=2px（p>0）上異于頂點的兩動點，且OA⊥OB，求△OAB周長的最小值.

探究5 如圖1，O是直角坐標原點，A，B是拋物線y2=2px（p>0）上異于頂點的兩動點，且OA⊥OB，求證直線AB與x軸相交于定點，并求定點坐標.

其解法見求軌跡方程解法3.

探究6 O是直角坐標原點，M（2p，0），過點M作直線交拋物線y2=2px（p>0）異于頂點的A，B兩動點，則OA⊥OB.

把B19代入B20，得y2-2pty-4p2=0.

所以y1+y2=2pt，y1y2=-4p2.

探究5與探究6互為充要條件.

探究7 O是直角坐標原點，T是拋物線y2=2px（p>0）上的定點，過T作拋物線兩條互相垂直的弦TA與TB，A，B都異于原點，則直線AB過定點.

證明 設T（2pm2，2pm），A（2pa2，2pa），B（2pb2，2pb），其中m為常數(shù)，a+b≠0.

所以（2pa2-2pm2）（2pb2-2pm2）+（2pa-2pm）（2pb-2pm）=0.

即（a+m）（b+m）+1=0.

則ab+（a+b）m+m2+1=0.

則ab=-（a+b）m-m2-1.

化簡，得（a+b）y=x+2pab.

則（a+b）y=x+2p［-（a+b）m-m2-1］.

則（a+b）（y+2mp）=x-2p（m2+1）.

故直線AB過定點Q（2p（m2+1），-2mp）.

探究8 如圖1，O是直角坐標原點，A，B是拋物線y2=2px（p>0）異于頂點的兩動點，且OA⊥OB，過A，B分別作拋物線的切線，則兩切線交點在定直線上.

由兩切線方程聯(lián)立求解得x=-2p.

故兩切線交點在定直線x=-2p上.

探究9 O是直角坐標原點，A，B是拋物線y2=2px（p>0）異于頂點的兩動點，過A，B分別作拋物線的切線，若兩切線的交點在直線x=-2p上，則OA⊥OB.

又x=-2p，

所以y1y2=-4p2.

所以OA⊥OB.

探究10 已知雙曲線的中心為O，實軸、虛軸的長分別為2a，2b（b>a>0），A，B分別為雙曲線上的兩點，且OA⊥OB.

（2）求△AOB面積的最小值.

將雙曲線的直角坐標方程化為極坐標方程，得

（2）由（1）知

4 溯源教材，升華思想

波利亞在《怎樣解題》一書中寫道：“好的題目和某種蘑菇有點相似之處，它們能成串生長，找到一個以后，再四處看看，很有可能在附近的地方能找到更多.”

題1 如圖2，直線y=x-2與拋物線y2=2x相交于A，B兩點，求證：OA⊥OB.

題1是人教版（2004年6月第1版）全日制普通高級中學教科書（必修）《數(shù)學》第二冊（上）第八章圓錐曲線方程第126頁小結(jié)與復習例2，課本給出了該題的兩種證法.

人教A版（2007年2月第2版）普通高中課程標準實驗教科書《數(shù)學》選修2-1第二章圓錐曲線與方程第73頁習題2.4第6題也是該題，只是給出的形式不同，一個是例題一個是習題.

題2 如圖3，已知直線與拋物線y2=2px（p>0）交于A，B兩點，且OA⊥OB，OD⊥AB交AB于點D，點D的坐標為（2，1），求p的值.

題2是人教A版（2007年2月第2版）普通高中課程標準實驗教科書《數(shù)學》選修2-1第二章圓錐曲線與方程第80頁復習參考題B組第3題.

人教A版（2020年5月第1版）普通高中教科書《數(shù)學》選擇性必修第一冊第三章圓錐曲線的方程第145頁第10題也是該題.

題3 經(jīng)過拋物線y2=2px（p>0）的頂點O任作兩條互相垂直的線段OA和OB（點A，B均在拋物線上），以直線OA的斜率k為參數(shù)，求線段AB的中點M的軌跡的參數(shù)方程.

題3是人教A版（2007年1月第2版）普通高中課程標準實驗教科書數(shù)學選修4-4《坐標系與參數(shù)方程》第二講參數(shù)方程第34頁習題2.2第5題.

題4 已知橢圓的中心為O，長軸、短軸的長分別為2a，2b（a>b>0），A，B分別為橢圓上的兩點，且OA⊥OB.

（2）求△AOB面積的最大值和最小值.

題4是人教A版（2007年1月第2版）普通高中課程標準實驗教科書數(shù)學選修4-4《坐標系與參數(shù)方程》第一講坐標系第15頁習題1.3第6題.

5 結(jié)束語

高中數(shù)學學科核心素養(yǎng)包括數(shù)學運算、邏輯推理、直觀想象、數(shù)學建模、數(shù)據(jù)分析、數(shù)學抽象.對課本例習題進行多解多變有利于發(fā)展學生的思維品質(zhì)，從而獲得正確的數(shù)學觀念，增進科學態(tài)度和責任.教師不僅要結(jié)合教學實際情況創(chuàng)設多種探究情境，以此激發(fā)學生的學習動機，還要通過積極改進和創(chuàng)新，引導學生大膽嘗試，養(yǎng)成敢于批判質(zhì)疑和勇于創(chuàng)新的精神.對于學生獨特的解決問題的方法，教師更應該重視，適時給予鼓勵，讓學生體驗成功的喜悅，激發(fā)學生的創(chuàng)造熱情，最終達到發(fā)展學生核心素養(yǎng)的目的.

參考文獻：

［1］周賽龍，儲炳南.對一道課本例題的再發(fā)現(xiàn)[J].中學數(shù)學研究（廣東），2021（15）：24-27.

［2］ 彭光焰.對一道課本例題的解法探討［J］.數(shù)理化解題研究，2022（34）：15-18.