巧用數學思維解初中物理題

張麗娟

【摘要】在中學物理學習過程中，特別是涉及較為復雜的問題時，往往會陷入困境.這主要是由于學生沒有把握問題的實質，因此要引導他們學會多種解題方法，尤其是要學會利用數學的概念來解決物理問題，注意訓練學生的思考能力，全面訓練他們的思維，使學生解決問題的能力得到提升.本文對初中物理教學中應用的幾種思想進行歸納和總結，以期對初中學生解決問題起到一定的指導作用.

【關鍵詞】數學思維；初中物理；解題技巧

將數學原理運用于中學物理教學中是一項具有挑戰性的任務.然而，運用數學思想解決物理問題在初中階段還比較少見，在高中的課本、習題、競賽試題等方面，卻處處可見運用數學思想的痕跡.這就要求在對物理概念、圖像和模型有清晰的認識的基礎上，選取合適的研究對象，對物理問題進行分析和解決[1].如果學生掌握數學思想的思維方法，就會更主動，眼界也會更寬，對自己所學的知識也會有更深刻的了解，在求解問題時，可以啟發自己的解題思路，從而發現一種十分簡潔而又高效的解決問題的方法.

1 比例思維

所謂“比例思維”，就是將相同的物理變量在各種條件下，通過比率對某些物理參數進行約化，減少中間的聯系，凸顯主要因素，使得計算過程變得簡單快捷[2].

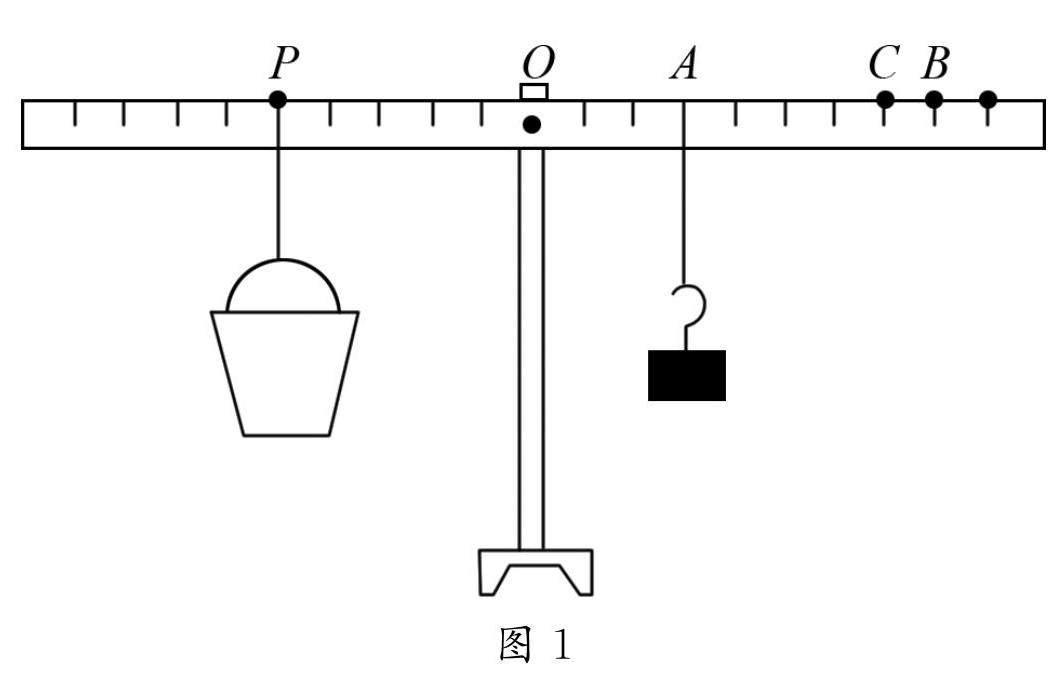
例1 小文在使用一把平衡尺（標明等距刻度的起始位置為等長的橫檔）.從圖1中可以看出，先將一個空的水桶吊在刻度線P上，將重量50克的掛鉤吊在刻度線A上，使操縱桿處于水平狀態.在不更換吊瓶的情況下，將吊瓶裝入半桶水，將吊瓶吊到刻度線B，控制桿處于水平狀態，使其處于平衡狀態.將桶中的水全部倒出，再往里面倒半桶水，然后將桶懸在刻度線P處，將鉤子懸在刻度線C處，這樣就可以使操縱桿始終處于水平狀態.由此可測得該種液體的密度是kg/m3.

分析與解 想要得到流體的濃度，必須掌握流體和水的容積相等，運用杠桿定律，通過推導出相應的等式來解決.

設空桶的重力為G1，水的重力為G2，液體的重力G3，鉤碼的重力為G4，由F1×L1= F2×L2，則G1+G2×OPG1×OP=G4×OBG4×OA ?G2G1=OAOB－OA ①，G1+G3×OPG1×OP=G4×OCG4×OA ?G3G1=OAOC－OA ②，由①②得，G3G2=OC－OAOB－OA=45，又G=mg=ρVg，且V相同，故ρ液ρ水=G3G2=45，即ρ液=45ρ水=45×1.0×203kg/m3=0.8×103kg/m3.

2 極限思維

所謂的“極限思維”就是依據相關的物理法則，在一定的范圍內，把其所包含的變量進行適當的擴展，將這些變量的數值（通常是指其極限值）進行對比，作出相應的判定[3].

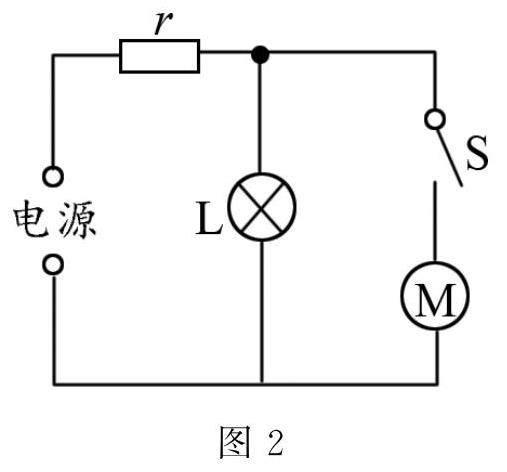
例2 家用線路的導線都帶有一些阻抗（大約為數歐），所以當家中使用高功率的家電，如空調或電爐時，家中原本亮著的燈泡將會變成黑色.在“創造素養實踐行”的過程中，一位學生經過試驗，能夠估計出家中電路導線部分的電阻，如圖2所示，將家用線路導線部分的總電阻設為r，L是一個普通的家用白熾燈泡，M是一臺空調器.在試驗過程中，首先將開關S打開，然后再將燈泡L打開，測量出在燈泡上的電壓為U1，而燈泡的功率為P1；再次關閉開關S，測量出在電燈泡上的電壓是U2，而空調器的電力是P2（P2＞P1）.試寫出估算r的表達式（只用U1、U2和P1表示設電源電壓恒定）.

分析與解 當S被切斷時，電燈泡和輸電線成了一個串聯，因為電燈泡的電阻比輸電線的阻值大得多，所以輸電線的電壓分壓效應可以不考慮，也就是U電源=U1.如果將開關S關閉，則將空氣調節器與電燈泡并聯，然后再與輸電線串聯，因為空氣調節器的電力比電燈泡的電力要大得多，所以在粗算時，電燈泡的能量可以不計，但是要把電力線的電阻和電壓分壓的影響加以考慮.即Ur=U1-U2，Ir=I空調，又P=UI，I=UR，則r=U1－U2P2U2=U1－U2·U2P2.

3 方程思維

所謂的“方程思維”就是通過構造一個包含待知變量的方程（或不等式），呈現其與已知變量之間的等價（或不等量）關系，從而解決待測變量[4].在物理學的求解中，要將問題所告知的已經知道的數量，運用物理法則來構建等式（或方程組），能讓問題變得簡單明了.

例3 正如在圖3（甲）中所示，木位于小塊B的上面木塊剛好浸入到水里.把金屬塊放在水里，容器底對金屬塊A的支撐力為2N；當木塊不動的時候，只有25的體積露出水面，見圖3（2）.可知木塊的體積是金屬塊的5倍，求出金屬密度和木塊的重力（g=10N/kg）.

分析與解 根據受力平衡分析，可列出三個等式方程.

F1=GA+GB

ρ水gVB=ρAVAg+ρbVBg ①，

FB=GB

ρ水g1－25VB=ρBVBg ②，

FA+F支=GA

ρ水gVA+F支=ρAVg ③，

由②得ρB=0.6×103kg/m3 ④，

又VB=5VA ⑤，

將④⑤代入①得ρA=2×103kg/m3，

將ρA代入③得

GA=2×10-4kg/m3×5×2×10-4m3×10N/kg=6N.

4 結語

從上面的例題可以看出，如果能靈活地使用數學思維將有關的物理定律和方程式合理地組合起來，并且從多個方面來思考解決問題的方法，能夠使學生們的物理思想更加靈活.但是任何一種思維方式都存在著一定的限制，如果在課堂上做大量的習題，而忽視對學生思考能力的培養與提升，那么就會適得其反.在日常的物理教學與比賽指導中，要注重對學生解決問題的思考能力的培養與提升.

參考文獻：

[1]丁海生.初中物理教學中拓展數理融合路徑的實踐舉隅[J].廣西物理，2023，44（03）：137-139.

[2]尤長江.探尋初中物理學習中正確的解題思路[J].科教文匯（中旬刊），2020（05）：139-140.

[3]黃宏鵬.淺談應用數學處理物理問題能力的培養[J].河南科技，2015（23）：264.

[4]朱坤燕.淺析數學方法在物理教學中的應用體現[J].才智，2015（36）：59.