初中幾何問題解題中的證明策略與方法研究
魏倩倩

【摘要】本文主要探討初中幾何問題解題中的證明策略與方法,具體涉及基本解題步驟和具體解題策略等方面的內容.文中簡要闡述初中幾何證明題的基本解題步驟,包括理解題目、分析已知條件、確定證明方向等.在此基礎上,提出善于挖掘及利用題目圖形中的隱藏條件、運用直接證明法進行幾何證明和利用反證法進行幾何證明三種具體解題策略.通過本文的研究,可以對初中幾何證明題的解題思路和方法進行總結和歸納,從而為學生解決幾何問題提供一定的參考.
【關鍵詞】初中數學;隱藏條件;解題策略
1 初中幾何證明題基本解題步驟
第一,理解題目是解題的第一步.仔細閱讀題目,了解所給條件和需要證明的結論.
第二,分析已知條件是解題的關鍵.將所給條件進行分類整理,確定已知條件之間的關系,并利用幾何知識進行推導和聯想.
第三,確定證明方向.根據題目中所給的結論,判斷證明的方法,常見的證明方法包括直接證明法、反證法、數學歸納法等.
第四,構建證明過程.根據已知條件和證明方向,運用幾何知識和推理方法,逐步推導需要證明的結論.在推導過程中,應注重邏輯嚴密,避免漏洞和錯誤.
2 初中幾何證明題的具體解題策略探討
2.1 善于挖掘及利用題目圖形中的隱藏條件
在解決初中幾何證明題時,善于挖掘和利用題目圖形中的隱藏條件是一種有效的解題策略.通過觀察和分析圖形,可以發現那些在題目中沒有直接給出但可以推導出來的條件,從而更快地得出證明結果.
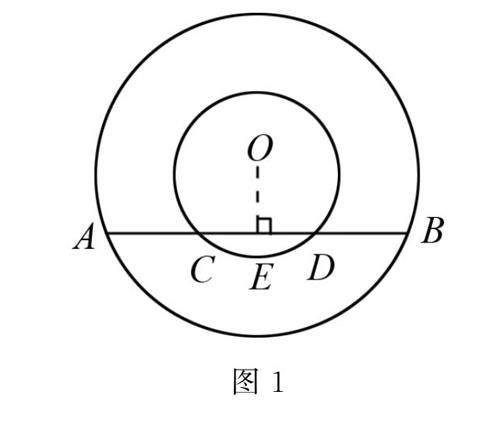
例1 如圖1所示,兩個圓都以點O為圓心,一條不過直徑的直線交外圓于點A、點B,與內圓相較于點C、點D,試證明AC=BD.
解析 首先可以通過觀察題目圖形尋找隱藏條件,在這個題目中,認真觀察發現兩個圓的圓心均為點O.根據圓的性質可知,OA=OB.盡管這個條件沒有明確給出,但它是一個隱藏條件,可以為后續的證明過程提供線索.
根據已知條件和圖形特點,可以使用直角三角形的性質來展開證明.過點O作AB的垂線,并連接OA,OB.在△AOB中,因為兩條邊OA和OB是外圓的半徑,所以△AOB是一個等腰三角形,由等腰三角形的性質可知∠OAB=∠OBA.
接下來,則需要找到與AC和BD有關的條件.觀察圖形可以發現,當連接點A和點B到點O時,可以得到Rt△AOE和Rt△BOE.這是另一個隱藏條件,可以作為進一步推導的線索.
考慮△OEC和△OED,它們的斜邊OC和OD分別為內部小圓的半徑,同樣根據圓的性質,△OEC和△OED都是等腰三角形.因此,CE=ED.
綜上所述,通過挖掘隱含條件,最終可以得到兩個關鍵的等邊關系:AE=BE,CE=DE,那么相應地可得到線段AC=BD,由此便完成了該幾何證明題的解答.
小結 通過以上分析,可以看到善于挖掘和利用題目圖形中的隱藏條件是解決初中幾何證明題的重要策略.通過觀察和發現隱藏條件可以引導證明的方向,加強證明過程中的推理和推導.
2.2 運用直接證明法進行幾何證明
直接證明法是解決初中幾何證明題最為常用的方法,是基于邏輯推理和已知條件,通過一系列明確的步驟來證明所要證明的結論.
例2 在△ABC中,AE作為△ABC外角的平分線,且有AE∥BC,試求證AB=AC.
解析 就該幾何證明例題而言,可以根據求證問題逐步考慮,循序漸進地求出最終結果.具體而言,在三角形中,證明兩條邊相等最為常用的方法便是證明對應的兩個角相等.如圖2所示,只要證明∠B=∠C,則可證明△ABC為等腰三角形,根據等腰三角形的性質便可以得出AB=AC的證明結論.
根據上述思路,首先可以結合已知條件“AE為△ABC外角的平分線”得出∠DAE=∠CAE.再次分析題目已知條件,即AE∥BC;結合平行線定理,可以由此推出∠DAE=∠CAE,∠C=∠CAE.
通過分析題目已知條件最終得出∠DAE=∠CAE,∠DAE=∠ABC兩個關系,整合后可知四個角都相等,即∠DAE=∠ABC=∠B=∠C,由此可知在等腰三角形ABC中,有AB=AC.具體的解答過程如下.
證明 因為AE為△ABC外角的平分線,
所以∠DAE=∠CAE.
因為AE∥BC,根據平行線定理可得∠DAE=∠ABC,
同時也可以推出∠C=∠CAE.
結合上述所推導出的等角關系,
可知∠DAE=∠CAE=∠B=∠C,
所以△ABC為等腰三角形,根據等腰三角形的性質可知其兩條腰長相等,
即AB=AC.
小結 經分析可知,在幾何證明題解答過程中,通常可以先結合題目已知條件進行逐步推導,將所推導出的內容進行整合,由此可以直接解決很多問題.
2.3 利用反證法進行幾何證明
利用反證法進行幾何證明是一種常見的解題策略,該方法通過假設所要證明的結論不成立,然后推導出矛盾的結果,從而得出所要證明的結論必定成立的結論.
例3 如圖3所示圓O中兩條非直徑弦分別為CD,AB,兩弦相較于點M,求證:AB與CD不能互相平分.
解析 此處以逆向思維假設AB與CD能互相平分,平分點為M點,由已知條件可知AB,CD均不是圓O的直徑,即相交點M并非圓心.連接OA,OB以及OM.根據既定假設條件,AB與CD相互平分,且平分點為M,那么有AM=BM,所以M應該是線段AB的中點,且根據圓的性質可知,OA和OB是圓的半徑,因此OA=OB,所以△AOB為等腰三角形.在等腰三角形中,底邊中點與頂點的連線即為三角形的高,所以OM⊥AB.同理,在△OCD中,M平分CD即為CD的中點,因為OC=OD,△OCD為等腰三角形.根據等腰三角形的性質可知,OM⊥CD.經分析可知,假設CD和AB平分于點M,那么過點M的兩條直線AB,CD都將垂直于M,而二者間本身相互矛盾,因此可知AB與CD可以相互平分的假設不成立,故AB與CD無法相互平分.
小結 在實際應用中,利用反證法進行幾何證明可以幫助我們深入理解圖形和已知條件,并且有助于發現問題中隱藏的規律和特點.
3 結語
初中幾何問題解題中,證明策略與方法是非常重要的.常用的證明方法包括直接證明法、間接證明法、反證法、數學歸納法等.在選擇證明方法時,需要根據已知條件和所求結論的性質進行綜合考慮,并靈活應用各種方法,通過多種方法的靈活運用,可以幫助學生有效地解答各類幾何證明題.
參考文獻:
[1]白方.幾何變換思想在初中幾何教學中的滲透與應用研究[D].上海:上海師范大學,2021.
[2]程香紅.問題提出教學法在初中幾何教學中的應用研究[D].上海:上海師范大學,2021.
[3]鄭高攀.化歸思想在初中幾何解題中的應用研究[D].漳州:閩南師范大學,2021.

