小學高年級數學單元互助式復習課教學策略的研究

張順積

內容摘要：單元整理復習課在小學數學教學中占有重要的地位，針對對現行的小學數學復習課教學的現狀和存在的問題，結合教學經驗和實踐，探究小學高年級數學互助式復習課教學策略。

關鍵詞：小學數學 ?互助式 ?復習 ?策略 ? 研究

復習課作為小學數學教學的重要課型之一，長期以來處于被忽略研究的范疇，《數學課程標準（2022年）版》指出：在教學中要重視對教學內容的整體分析，幫助學生建立能體現數學學科本質、對未來學習有支撐意義的結構化的數學知識體系，幫助學生用學會用整體的、聯系的、發展的眼光看問題，形成科學的思維習慣，發展核心素養。為了讓復習課煥發生機，我們結合教學實踐對互助式復習課進行了一些有益的探究，下面結合教學實踐，從四個方面探討單元互助式復習課教學的策略。

一、創設情境，激發學習動機。

在復習課中構建良好的教學氛圍、教學情境開展單元整理，更能吸引學生的注意力.提升性單元整理和復習教學的效率。在進行情境創設時可以利用游戲、詩歌、競賽、小組學習、學生講課等有利于學生“回想”的良好“問題情境”和多樣的教學形式活躍課堂氣氛，增強情境教學實質內容調動學生學習的積極性和主動性，增加師生之間互動與交流，幫助學生快速地掌握相關知識點促進學生邏輯思維能力的發展，促進復習走向深入。

二、互助梳理，串聯知識鏈。

傳統復習課，教師往往把目標定位在“查缺補漏”上，因而呈現給學生的是支離破碎的題目。因而要把復習課定位在“促進知識系統化”目標的實現上，交給學生一些梳理知識的方法，讓學生在學習過程中主動去整理，從而盤活學生認知體系。引導學生利用“整理復習單”“思維導圖”“結構框架圖”“樹狀圖”等方法進行回顧整理，激發學生對所學知識的合作梳理和盤活，提升學習能力。

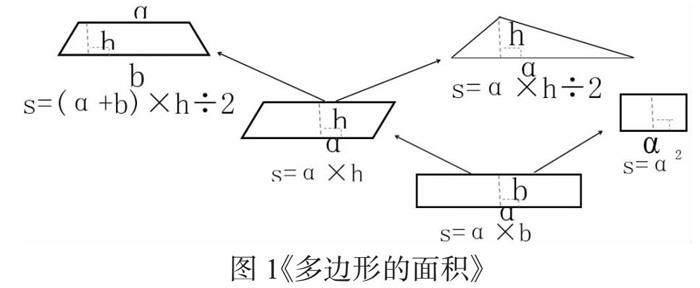
如在五年級的《多邊形的面積》整理和復習時，引導學生對求各種圖形面積公式的條件進行互助梳理，通過合作交流、探討匯報和補充完善，精煉構架出各種圖形之間的“樹狀”關系（如下圖1），從結構清晰的樹形圖中可以直觀的看出各平面圖形之間關鍵聯結之處，在這樣的過程中，學生自主理出了知識體系的根脈，有利于對對知識體系的深度把握和構建，對學生的興趣培養以及知識結構化建構大有益處。

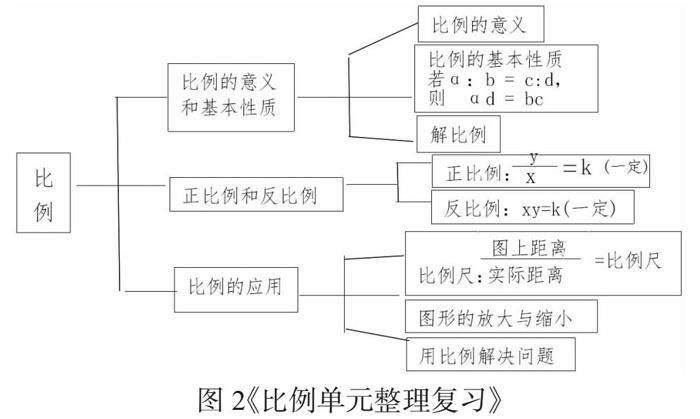
又如在六年級教學《比例單元整理復習》時，引導學生通過“辯一辯”“聯一聯”等過程自主創造知識鏈，通過互助合作、探索交流，促發思維碰撞，讓學生站在更高的起點完善認知體系，找到各知識之間溝通的紐帶和橋梁，進一步建立知識之間的縱橫聯系和相互作用，讓無序、松散的知識變得更加有序、系統，理解和感悟也更加通暢、深刻（如下圖2）。

三、理練融合，構建新認知。

在復習中把單元知識置于更廣闊的背景關系中，依據重難點、學生易錯點，通過變形，引申，發散等方式形成典型的例題，設計符合學生心理特點、洋溢著現代生活氣息的練習題，突出練習的典型性、實踐性、普遍性、層次性、綜合性和開放性，讓學生跳起來摘“果子”，在摘“果子”的過程中領悟方法，以“動”促“思”，在練習中感受到數學的價值。

如在《長方體和正方體的整理復習》中可這樣安排：出示一個長方體框架，然后啟發學生：“大家看到了什么？“如果它是一個游泳池，它的占地面積是多少？這是求什么？解答這個問題還必須知道什么條件？”“如果這是一個魚缸，請你結合自己的想象，本單元知識和生活實際，你能提出什么數學問題？請至少提出兩個問題，然后和同桌說一說你提出的數學問題要運用長方體或正方體的什么知識來解答。”這樣學生的思維一次次被激活，通過對不同問題進行分類比較，讓學生頓悟其中不變的知識和方法，即都可轉化成長方體的特征、表面積、體積的數學問題。在這一過程中，學生學會用數學眼光觀察、用數學思維思考、用數學語言表達，從而使數學素養得到提升。

四、應用貫通、提升數學素養。

蘇霍姆林斯基說過：“教給學生借助已有知識去獲取新知識，這是最高的教學技巧之所在。通過梳理串聯知識和練習鞏固，在應用中培養數學素養、使所學知識得到延伸和升華，激發學生的求職欲望和深度思考，讓學生在解決問題的過程中升華認知結構，提升高階思維。例如在教學《圓柱和圓錐的整理復習》時，在知識的實踐應用中圍繞南丹的白褲瑤生態博物館中的糧倉的建造，提出問題：這個糧倉可以看做由什么立體圖形組成？求糧倉的占地面積就是求什么？這個糧倉能容納多少糧食是求什么？這樣在解決生活實際問題的加深學生對圓錐與圓柱之間聯系的深層次理解和感悟，在落實核心素養的同時激發學生的高階思維，提升思維層次。

又如在教學“百分數整理和復習”時，為了增強學生對數量關系的理解和感悟，深度把握關系式中相應量之間的聯系，可以設計“一題多變”的問題串讓學生練習，如問題1：歡歡家用200kg稻谷碾出了150kg 的大米，她家稻谷的出米率是多少？問題2：笑笑家現在有稻谷500kg ，可以碾出大米多少千克？問題3：王明家用稻谷碾出大米96kg，求稻谷有多少千克？問題4：南丹巴平米的出米率在75%——80%之間，李青家有600kg稻谷，最多能碾出大米多少千克？若要確保碾出500kg的大米，應該準備多少kg的稻谷？在這樣的問題串中實現“練中求知，串知成鏈，深度練習，有機構建”的目的，切實提升練習實效，拓寬延伸學生的知識儲量。

綜上所述，數學復習課要充分體現“以學生發展為本”的教學理念，從學生已有的生活經驗和知識背景出發，在復習的過程中促使學生從學會變為會學，讓學生在開放互助、深度探究中清除知識的薄弱點、盲障點，在體會數學學習的魅力的積極情感體驗中促進學生的可持續發展。