情境啟發(fā)探究,合作促進創(chuàng)新
劉培杰
[ 摘 要 ]如何借助情境激發(fā)學生的探究興趣,讓學生在合作學習中形成良好的創(chuàng)新意識呢?文章以“銳角三角函數(shù)”的教學為例,從“創(chuàng)設情境,激趣啟思”“理性歸納,建構新知”“問題設置,促進遷移”“適當啟發(fā),拓展延伸”等方面展開教學,并談幾點思考:生活化的情境可激發(fā)探究欲,關聯(lián)問題可發(fā)展數(shù)學思維,互動交流是促進創(chuàng)新的動力,“問題化”總結新穎且有意義.
[ 關鍵詞 ]情境;探究;合作;創(chuàng)新
數(shù)學對發(fā)展學生的思維與創(chuàng)新能力具有重要作用.創(chuàng)設恰到好處的情境能觸動學生的內心,激發(fā)學生對知識的探索欲;和諧、民主的合作學習可發(fā)散學生的思維,促進創(chuàng)新意識的形成[1].為了驗證這種說法,筆者在這方面做了大量研究,現(xiàn)以“銳角三角函數(shù)”的教學為例,與同行交流.
教學簡錄
1.創(chuàng)設情境,激趣啟思
結合學生認知發(fā)展規(guī)律,初中數(shù)學課堂常用的情境有問題情境與思維情境等,這些情境都是激發(fā)學生學習興趣,使其產(chǎn)生探究行為,發(fā)展高階思維的重要舉措.同時,良好的情境會營造自由、民主的課堂環(huán)境,讓學生有更廣闊的表現(xiàn)空間.
情境創(chuàng)設 眾所周知,測算的應用十分廣泛,如測算隧道的方向、平行岸的寬度、飛機與地面的距離、月球和地球的距離……
如圖1,今天我們就一起來探討如何測算旗桿的高度.已知測架AD的高度為1米,你能根據(jù)圖中所標示的數(shù)據(jù)推算出旗桿EB的高嗎?
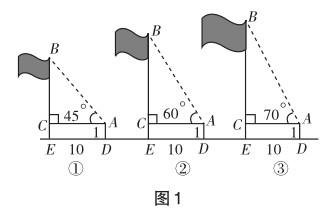
要求學生以小組合作學習的方式探討這個問題,每組派一名代表將組內研究成果展示出來.
組1:前兩幅圖可以推導出旗桿的高度,但第三幅圖不行.具體過程為:


組2:我們組贊同前兩幅圖的測算方法,但認為第三幅圖中的旗桿高度也能推導出來,且與前兩幅圖所用方法類似.既然∠CAB的度數(shù)是確定的,那么AC∶BC的值必然也是恒定的,旗桿高度就可以計算出來,但我們不知道計算方法是怎樣的.
組3:同意組2的觀點,問題是我們不會計算.
師:你們是如何確定當∠CAB的度數(shù)確定時,AC∶BC的值是恒定的呢?
生1:(操作幾何畫板)如圖2,已知Rt△ABC中的∠A為70°,無論點B與點C的位置在哪兒,AC∶BC的值恒定不變.
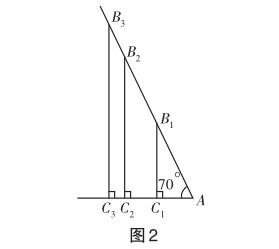
生2:即使知道它們的比值不變,也求不出旗桿的高度呀.
生3:若獲得AC∶BC的近似值,或許就能獲得BC的值.
師:很好!那有沒有辦法獲得AC∶BC的近似值呢?
生4:只要能測量出AC,BC的長度即可.根據(jù)圖2所顯示的原理,只要能準確地畫出任意一個三角形,并測出AC,BC的長度,那所獲得的比值與原圖是相等的.
在這種理念的驅使下,學生自主畫圖、取值、計算,發(fā)現(xiàn)當∠CAB為70°時,AC∶BC的值可能是無理數(shù),難以獲得精確值,那么計算而來的旗桿高度也只能取近似值.
2.理性歸納,建構新知

教師充分肯定了學生在上一個環(huán)節(jié)的表現(xiàn),并與學生再次確認當∠CAB=70°時,獲取旗桿高度的方法.接下來教師趁熱打鐵,要求學生分析“當∠CAB=41°時,BC∶AC的值也是確定的嗎”.學生一致表示確定.在此基礎上,教師設計了一張表格投影到電子白板上,讓學生填寫B(tài)C∶AC的值(見表1),并說說比值與∠A的關系.
生5:如圖3,通過畫圖并對應表格數(shù)據(jù)來看,BC∶AC的值會隨著∠A度數(shù)的變化而改變,若∠A確定了,那么BC∶AC的值就是恒定的,這與之前接觸過的函數(shù)關系一致,即BC∶AC可理解為∠A的函數(shù).


3.問題設置,促進遷移
問題是數(shù)學的心臟,數(shù)學學習離不開問題的引導.教師精心設計問題串,可讓學生從更深層次內化新知,形成技能,促進知識的遷移與創(chuàng)新意識的發(fā)展.
問題1 (1)在Rt△ABC中,∠C為直角,AC=15,BC=8,分別求∠A,∠B的三角函數(shù)值.
(2)在△CDE中,已知DE=6,CE=8,CD=10,試求∠D的三角函數(shù)值.
(3)已知△ABC中,AB=AC= 5,BC=6,求sin∠B,tan∠A.
分析 問題(1)需先確定斜邊的值;問題(2)需判斷△CDE是否為直角三角形;問題(3)需通過作高來構造直角三角形.這三個問題成功地開啟了學生的思維,讓學生通過問題的解決,進一步夯實了知識基礎.


師:是否能以BC為軸作對稱?(答案是否定的)想要獲得sin2α,必須求出x,y的值,該怎么求呢?
生7:可借助三角形相似與勾股定理來列方程組求解.
學生交流,并總結:sinα,cosα,tanα均為獨立的個體,符號不可隨意分割,不可將它們視作sin?α,cos?α,tan?α. sin 2α≠2 sin α,同理,tan(α+β)≠tanα+ tanβ.
學生的思維非常活躍,對這部分知識的理解相當透徹.此時,教師要求學生思考本節(jié)課為什么要研究直角三角形的銳角三角函數(shù),并分析其本質、求解注意事項等.
4.適當啟發(fā),拓展延伸
師:大家對本節(jié)課的教學還存在什么想法與問題嗎?
此問意在讓學生通過對本節(jié)課的回顧、總結、反思,提出自己的看法.在這個問題的啟發(fā)下,學生提出如下疑惑:①為什么直角三角形的銳角存在三角函數(shù),而鈍角與直角卻不存在三角函數(shù)呢?②41°,70°的三角函數(shù)值能準確求出來嗎?③要測量一座山的高度,但無法進入山底,該怎么構造直角三角形呢?④地球與月球的距離那么遠,是否可以通過構造直角三角形來解決距離問題呢?
學生所提出的每一個問題都具有現(xiàn)實研究意義,由此也可以看出學生處于思考的狀態(tài),這是促進創(chuàng)新的基礎.當然,課堂時間是有限的,教師不可能在課堂上逐一探討每一個問題.因此,筆者挑選出幾個具有代表意義的問題要求學生課后查閱資料、合作交流,爭取自主答疑解惑.
教學感悟
1.生活化的情境可激發(fā)探究欲
生活化的情境與學生的生活息息相關,以此作為教學的起點,往往能成功激發(fā)學生的探索欲.測量旗桿的情境源自學生的實際生活,學生雖然都見過旗桿,卻從來沒有想過要測量它的高度,這個情境成功地激起了學生的探索興趣,讓學生對本節(jié)課充滿了渴望.
2.關聯(lián)問題可發(fā)展數(shù)學思維
面對情境中呈現(xiàn)的三幅圖,學生經(jīng)過自主探索發(fā)現(xiàn)前兩根旗桿的高度能順利求出,但第三根旗桿卻無法快速求出,由此引發(fā)了AC∶BC是否為確定值的問題,近似值也自然生成.該情境成功引起了學生的認知沖突,讓學生產(chǎn)生了更多思考,創(chuàng)新意識也在思維的不斷深化中萌發(fā).通過合作交流與探索,學生不僅發(fā)現(xiàn)了蘊含其中的規(guī)律,還體驗到了學習帶來的愉悅,建立了學習信心.
3.互動交流是促進創(chuàng)新的動力
教師著重應用合作交流的方式進行授課,學生積極思考,表達自己的觀點,各組將組內成果與大家共享,加速了解決問題的進程,也優(yōu)化了學生的思維,讓信息加工變得更為深入[2].學生的群體認知隨著交流的深入變得更加深刻,這不僅刷新了學生原有的知識,還幫助學生建構了新的知識網(wǎng)絡,這是傳統(tǒng)“注入式”教學無法達到的教學成效.交流時,師生、生生積極地表達自己的觀點,呈現(xiàn)出較多的思維亮點,作為教師,不僅捕捉到了學生的發(fā)光點,還給予積極的引導與啟發(fā),開啟了學生的思維,激發(fā)了創(chuàng)新意識,高質量課堂也在互動中動態(tài)生成.
4.“問題化”總結新穎且有意義
課堂尾聲,在教師的啟發(fā)下,學生自主提出一些高質量且具有探究價值的問題,讓課堂總結顯得新穎且有意義.“問題化”的課堂總結不僅引發(fā)了學生的思考,也引起了筆者的反思:究竟該如何滿足學生的好奇心?通過怎樣的方式才能有效提升學生的思維品質?
總之,精心創(chuàng)設教學情境為學生的探究搭建了良好的平臺,自主探索與合作交流是開闊學生視野、促進學生掌握新技能、提煉學習方法、積累學習經(jīng)驗的重要方式.情境啟發(fā)探究、合作促進創(chuàng)新的課堂充滿了靈氣與智慧,是促進學生全面發(fā)展的重要途徑.
參考文獻:
[1]馮衛(wèi)東.“自學·議論·引導”教學法的基本原理與操作要義[J].課程·教材·教法,2011,31(05):43-48.
[2]唐懷萍,都日娜.探究小組合作下初中數(shù)學糾錯能力實施策略[J].數(shù)學學習與研究,2019(17):86.

