數學教育中的情境研究：回顧與展望

鄭蓉蓉 蔣逸卿 唐恒鈞

摘 要：在基礎教育課程改革的背景下，我國數學教育中的情境研究逐漸升溫。其中，情境及相關概念的研究表明，情境具有社會屬性與認知屬性，其高頻相關概念主要有數學情境、問題情境、教學情境等；情境的功能與價值研究表明，情境是發展和評價數學核心素養的載體、培育非智力因素的觸發點、培養問題解決能力的實踐場等；情境的創設和使用研究重點關注創設的原則和策略、使用（教學）的基本模式以及試題與作業中的情境設計等。展望未來，數學教育中的情境研究要進一步關注不同語境下情境的內涵與特征，建構作業和試題中情境的操作體系，探索情境與智慧教育的融合。

關鍵詞：數學教育；情境；數學情境；問題情境；教學情境

本文系全國教育科學“十三五”規劃教育部重點課題“指向深度理解的‘問題鏈教學研究”（編號：DHA200318）、浙江省教育廳一般科研項目“學習進階視域下的數學作業鏈式設計”（編號：KYZ34423205）的階段性研究成果。

情境在數學教育中得到關注與研究已有30余年。隨著課程改革的不斷推進，“生活化”“情境化”成為熱詞。^［1］2019年，中共中央、國務院頒布的《關于深化教育教學改革全面提高義務教育質量的意見》特別指出“重視情境教學”，這是“情境教學”首次被寫進重大決策文件。^［2］《義務教育數學課程標準（2022年版）》（以下簡稱“義教課標”）強調引導學生在真實情境中發現和提出問題。可見，情境在數學教育中的價值與功能得到不斷凸顯。為了更好地開展情境教學，強化情境對核心素養培養的作用，有必要系統梳理我國數學教育中情境的相關研究，明晰新課程改革背景下情境研究的方向。

一、數學教育中情境研究的概況

在中國知網（CNKI）中以“情境”并含“數學”為篇名進行學術期刊檢索，再根據如下兩條標準剔除無關文獻：一是文章主題為普通中小學的數學教與學，排除關于幼兒園、職業中學、大學的文章；二是作者是中小學教師、教研員、高校教師和研究所、出版社研究人員，排除中小學生寫的文章。據此標準，檢索到1992年—2023年（8月）期間發表于學術期刊的文章共1360篇，其中2000年以來的有1339篇，占98.5%；1992年—2023年（8月）期間發表于核心期刊的文章共172篇，其中2000年以來的有164篇，占95.3%。因此，本研究主要以2000年以來的文獻為研究對象。

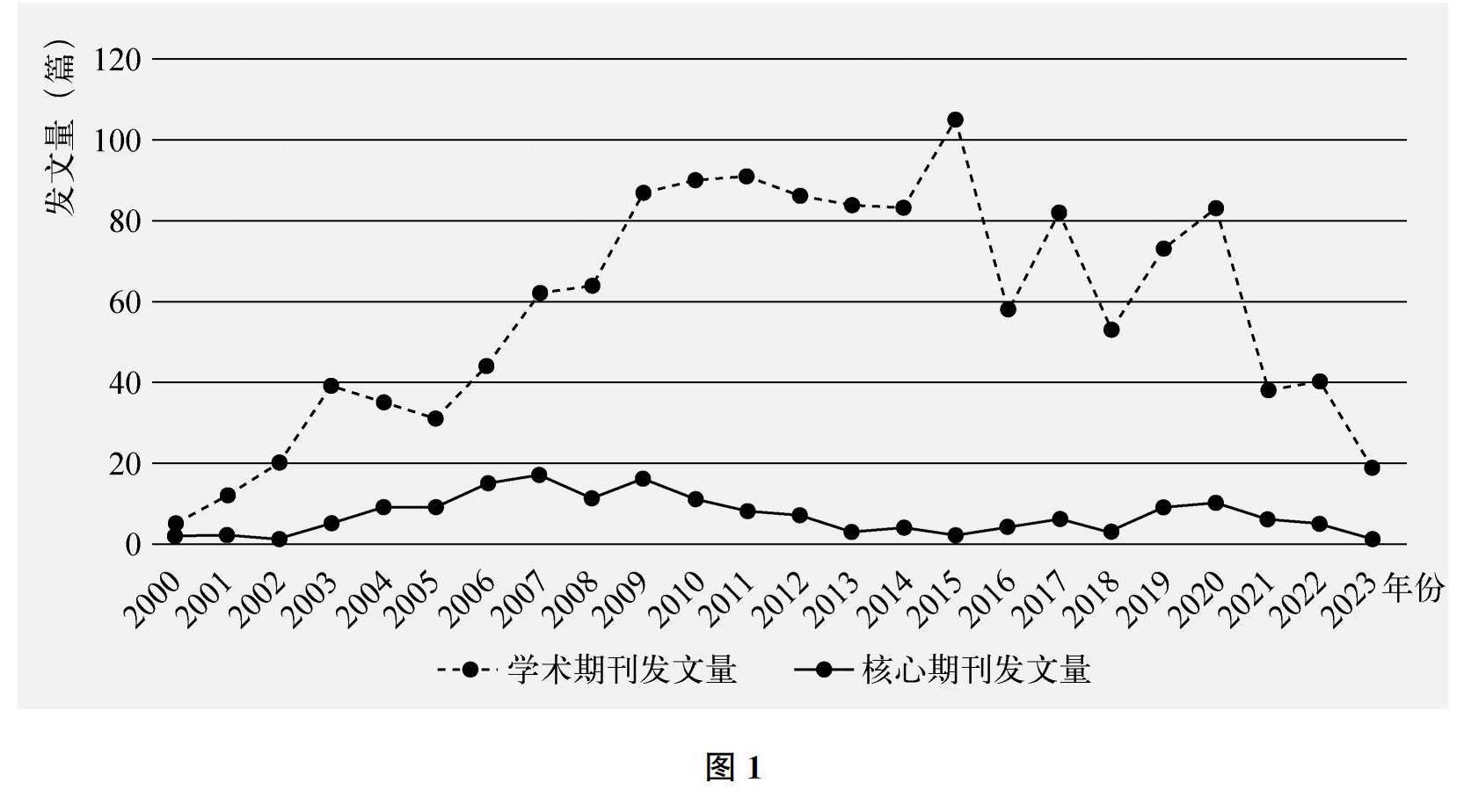
圖1顯示了2000年以來學術期刊、核心期刊上發表的文章的年度數量，這在一定程度上反映了數學教育界對情境研究的關注趨勢。可以看出，自2001年國家啟動基礎教育課程改革以來，數學教育中的情境研究逐漸引起關注，其中有兩個快速增長期，分別為2006—2010年與2018—2020年，2007年與2009年出現兩個小高峰，2018年以后又迎來新的研究高潮。這兩個時期的變化與2006年義務教育階段的課標啟動修訂以及2018 ??年高中階段的課標頒布新版緊密相關。

分析這二十多年間數學教育中的情境研究，其成果主要涉及以下幾個方面：首先，關于數學教育中情境的內涵與特征及相關概念辨析。比如，呂傳漢、汪秉彝關注情境的社會屬性與認知屬性，從情境的社會學和心理學角度出發，提出數學情境是數學概念產生的背景，也是發現、提出、分析、解決數學問題的前提、基礎和條件。^［3］其次，關于情境的功能與價值。可以概括為發展和評價數學核心素養的載體、培育非智力因素的觸發點、培養問題解決能力的實踐場等。比如，常磊、鮑建生提出借助情境可以還原數學知識的抽象過程，幫助學生理解所學數學知識，為數學抽象素養的形成提供“理解”前提。^［4］最后，關于情境的創設和使用。主要包括情境創設的原則和策略、使用的基本模式、試題與作業中的情境設計。比如，黃翔、李開慧強調情境化設計需處理好形式與實質、情境與情景、情境化與系統性等方面的關系。^［5］

二、數學教育中情境相關概念的辨析研究

《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱“高中課標”）和義教課標均未界定“情境”概念。前者根據認知活動信息來源的不同，將情境分為現實情境、數學情境和科學情境三類；后者根據認知活動信息來源的不同，提到了真實情境、實際情境、現實情境、生活情境、社會情境、數學情境、科學情境、科技情境、模擬情境等概念，并且特別強調了真實情境。數學教育文獻中關于情境內涵與特征的研究也相對較少，往往是在“數學情境”“問題情境”“教學情境”等詞中使用“情境”。因此，以下對我們統計的數學教育研究文獻中出現頻次最高的數學情境（319次）、問題情境（343次）、教學情境（602次）進行分析，以期為數學教育中情境的理解提供線索。

（一） 數學情境

國內學者對“數學情境”含義的闡述，一般都建立在情境概念的社會屬性和認知屬性之上。比如，如上文所述，呂傳漢、汪秉彝立足兩種屬性的統整角度，給出數學情境的含義。此外，呂昌旭、汪秉彝基于情境的社會屬性指出，數學情境是從事數學學習活動的環境、產生數學行為的條件。^［6］夏小剛、汪秉彝將情境視為人類認知活動的信息來源，進而將數學情境界定為含有相關數學知識和數學思想方法的情境及數學知識產生的背景。^［7］

由此，我們首先要認識到數學情境的社會屬性，即數學情境是學生社會行為產生的條件，表現在數學教學中是學生從事學習活動、產生學習行為的環境條件；其次要關注到數學情境的認知屬性，即數學情境是認知活動的信息載體，含刺激要素，是課堂教學中學生充分參與、積極建構、發現問題、提出問題、分析問題和解決問題的先決條件。

（二） 問題情境

“問題情境”具有多重含義，也使情境的含義變得更加豐富。對有關“問題情境”含義的代表性觀點整理概括后，將其歸納為兩個認識視角——情境指向和問題指向。^［8］前者將問題情境的落腳點定位在學習環境、心理困境等具有情感和認知因素的環境上。比如，問題情境是學生參與數學活動所處的學習環境 ^［9］；是有目標而無法獲得實現途徑的心理困境^［10］；是一種能夠引發產生問題并解決問題的情境^［11］。后者則將著力點放在具體問題和教學任務等上。比如，邱家寰認為問題情境是學生付出一定的努力后方可完成的教學任務^［12］；周先榮、張國棣定義問題情境為教學中專門針對某一部分內容設置的具體問題^［13］。任旭、夏小剛認為這些認識在一定程度上凸顯了某一視角的重要作用，卻忽略了對兩種指向的整合，基于此將問題情境定義為一類具有現實性和思考性的數學問題。^［14］這種定義在一定程度上整合了兩種視角，但是重心仍然落腳在數學問題上。

事實上，問題情境定義的多樣化源于其適用領域的廣泛性。在數學教學中，問題情境的創設受教學目標和教學實際需要的制約。設立教學任務（具體問題）的目的是由問題產生情境，在情境中引發學生思維的參與，以此培養學生主動發現問題、提出問題、分析問題、解決問題的能力，因此，凸顯問題情境的情境指向可能更能反映其價值所在。而在數學教材中，問題情境的設置強調以不同類型的情境為載體，以呈現問題為主要目的，因此，突出問題指向更具意義。綜上，在不同的領域，因不同的目標和需要而側重問題情境定義的不同方面，這或許也是一種整合的表現形式。

（三） 教學情境

現有“教學情境”的定義，主要建立在對其結構要素基本屬性的揭示及外在表現形態的反映上。根據結構功能主義的觀點，教學情境由情境主體、情境資源、情境空間、情境時間四個基本要素構成，要素的不同組合形式會呈現出具有不同功能的表現形態。^［15］比如，張輝蓉、朱德全認為，教學情境為課堂教學中，利用具體的場所（教室環境）、景象（教學內容）、境況（學生心境）等，引起學生的情感體驗，解決學生認知過程中的形象與抽象、實際與理論、感性與理性以及舊知與新知的關系和矛盾的師生互動關系的載體。^［16］李鵬鴿認為，教學情境指知識得以存在和應用的環境或活動背景，可分為“境”（認知錨點）和“情”（情感前提）兩個維度。^［17］可以發現，這兩種定義兼顧了教學情境結構要素的基本屬性和外在表現形態，前者關注情境空間、情境資源、情境主體三個要素與教學情境的主體體驗水平，后者聚焦情境資源、情境空間兩個要素與教學情境的認知、情感態度的目的取向。

早期的研究者往往更關注情境所具有的功能性表現形態。比如，李吉林對教學中容易被忽視的人文、情感、態度等因素進行研究，構建出獨具特色的情境教學理論體系，這是在把握包括教學情境的存在場域、主體體驗水平等通常意義上藝術性價值取向的基礎上形成的。^［18］呂傳漢、汪秉彝的“情境問題”教學模式則源于對教學情境中主體體驗水平的認識，即動機性情境可以引發主體學習數學的興趣，激發好奇心、發現欲，而問題性情境則在前述體驗水平上喚醒主體的問題意識，從而培養發現、提出、分析和解決數學問題的能力。^［19］

由此，可以認為教學情境是由主體、資源、空間、時間四個基本要素構成的具有多重功能性表現形態的情境，在教學實踐中往往需要關注它在多種功能取向下對主體的價值，以便發揮它應有的功效。

綜合上述分析，不難發現，數學情境和問題情境繼承了教學情境的四個基本要素，是教學情境具體功能性表現形態的有機組合。數學情境具有的社會屬性和認知屬性正來源于教學情境的主體體驗性和認知取向，問題情境則主要反映了教學情境中主體的三種體驗性水平。

三、數學教育中情境的功能與價值研究

（一） 發展和評價數學核心素養的載體

高中課標提出了數學抽象、邏輯推理、數學建模、數學運算、直觀想象和數據分析這六大數學核心素養。國內外研究者對情境在培育數學核心素養過程中的重要性有一致的判斷：數學教學應注重情境與各個數學核心素養之間的深刻關系，并探索如何充分發揮情境在發展數學核心素養方面的載體功能。數學學習往往要經歷高度抽象的過程，借助情境可以還原數學知識的抽象過程，幫助學生理解所學數學知識^［20］，為數學抽象素養的形成提供“理解”前提；邏輯推理依據的“事實”“命題”“規則”皆來源于現實情境和數學情境，通過情境載體階段性、漸進性地滲入邏輯推理思維模式^［21］，在歸納和類比中發現和提出新命題，在演繹推理中分析和解決情境中的問題，培育邏輯推理素養；數學建模是從現實世界到數學領域的映射^［22］，學生運用數學情境中的語言、知識、思想和方法構建模型去描述、解決現實情境中的問題時，現實情境和數學情境兩個維度必然深度參與其中。在教師逐步增加情境中真實且復雜的因素、學生逐漸拓展情境中數學信息的廣度和深度（習得愈加豐富的數學知識和方法）的過程中，一個良性的素養發展圈慢慢形成。學生在這當中反復經歷愈發真實的數學建模活動，積累數學建模經驗，形成數學建模素養。

核心素養涉及的是高階思維、復雜的認知能力以及在新的情境中解決問題的能力等關鍵學習結果。^［23］因此，傳統的標準化紙筆測試無法滿足核心素養評價所需要的準確性、綜合性，而表現性評價的運用為指向核心素養的評價指明了方向。表現性評價是對內在能力或傾向在具體情境里的行為表現的評價^［24］，與情境高度關聯，其實施主要依賴于學生在情境中的表現信息。由此可見，情境不僅對數學核心素養的培育具有重要意義，而且與指向數學核心素養的表現性評價高度相關。

（二） 培育非智力因素的觸發點

非智力因素是指智力因素以外的心理因素，一般包括動機、興趣、情感、自我效能感等。^［25］眾多研究表明，非智力因素在數學學習中起著重要的作用^［2629］，數學教學要注意非智力因素的培養。情境對學生激發數學學習的興趣和動機、感受數學學習的意義以獲得自我效能感，有顯著作用。^［30］一方面，在真實完整的情境中，新舊知識或經驗的沖突以及解決現實問題的渴望會引發學生強烈的學習興趣和動機，讓學生進入主動的“思維場”。^［31］另一方面，情境拉近了數學與現實生活及其他學科的距離，讓學生在發現問題、解決問題的過程中，深切體會到數學學習的意義，提升自我效能感，這也在一定程度上增強了學生學習數學的積極情感。

（三） 培養問題解決能力的實踐場

PISA2012將問題解決能力分為理解與提取問題的能力、表征與分析問題的能力、計劃與解決問題的能力、監控與反思問題的能力。^［32］有研究者指出，分析情境是否能夠促進問題解決能力的培養需要關注三點：培育具有主體意識的思維和行動、合法的邊緣性參與、建構實踐共同體。^［33］情境能夠喚醒主體的問題意識，從而引發學生思維的參與，進而發展理解與提取問題、表征與分析問題、計劃與解決問題的能力。面對抽象程度過高、數學關系復雜的知識或問題時，情境往往能夠作為數學學習的腳手架，將學生熟悉的具體對象與高度抽象的知識、問題相關聯，從而降低理解的門檻，使處于“邊緣地帶”的學生也能參與到學習活動中，并且逐步進入核心，在實質性參與中提高問題解決能力。不管是數學情境的社會屬性、問題情境的情境指向、教學情境的空間結構要素，還是情境本身所具有的“環境”意蘊，無不反映情境促使學生之間產生無形的相互需求（包括解決問題、情感共鳴），引導實踐共同體的產生，讓學生在互動合作中生成并共享經驗，分析并反思方法，促進問題解決能力的提升。

四、數學教育中情境的創設與使用研究

（一） 情境創設的原則

情境創設的原則需要立足現實生活、數學學科和學生這三個要素來提煉。現有研究認為，在創設過程中需要把握好幾對關系：

一是形式與內容的關系。情境的內容應基于數學學科本質，且貼近學生現實。一方面，情境的創設應與所學數學內容緊密關聯，且具有鮮明的目標指向^［34］；另一方面，情境的創設需注意不同發展階段、不同文化背景學生的經驗基礎。因此，情境作為一種內容的呈現方式，其形式應由內容所決定，而非一個遠離數學本質或脫離學生實際的貼著生活標簽的空虛外殼。

二是情境與情景的關系。黃翔、李開慧在內涵和來源方面區分了情境與情景。^［35］情境內涵更豐富，常處于動態并促使數學課堂具有自我生長性的立體環境；情景一般指數學問題的生活背景素材。由此可見，情景在某些情況下是情境創設的前提——對數學問題設置生活情境需要相關的生活背景素材作為支撐——當然，情境素材的來源并不局限于現實生活，還包括數學學科本身和其他學科。此外，更重要的是情境具有生成性，情境可以和問題互相動態生成，從而將數學教與學融合為一體。

三是情境化與系統性的關系。當前，有不少關于“去情境”教學的探討。^［36］這反映的是學者和教師對數學情境化與系統性（形式化數學內容之間的聯系）關系的一種反思，即如何調適數學教學中的生活化、情境化使其不沖淡應有的“數學味”。創設情境的主要目的是實現數學化（形式化）活動過程的順利轉化，而過于生活化、情境化的素材必然裹挾著大量非數學的干擾因素。因此，情境化、生活化都要把握一個合理的度，根據具體問題和教學目標在情境化和系統性之間尋求平衡。^［37］

（二） 情境創設的策略

情境創設的有效程度影響數學教學的效果。有研究發現，一線教師存在情境創設流于形式、機械性運用情境，導致無法引導學生建構意義等狀況。從根本上說，這些都源于教師對情境創設有效性認識的不足。對此，眾多學者和教師從設計方式和素材來源等角度討論了優化情境創設的策略。

吳黎貞認為應根據教學需要創設與教學內容相適應的場景，提出在數學教學中創設“懸念型”“故事型”“游戲型”“類比型”情境的策略，以此激發學生興趣、發展學生思維。^［38］吳華、馬東艷根據學生具體情況，從教學需要入手，結合多媒體信息技術，創設數學教學多元情境，豐富了情境創設的方式。^［39］劉允忠從素材來源的角度，提出可以從實際生活、相關學科、新聞事件、諺語故事、古典數學文化、類比猜想、操作實驗中創設情境。^［40］張秀花站在教學實踐的立場，給出一系列有效教學情境創設的策略，如：要有利于激發課堂聯想與思考，要激勵學生自主創設，要強化主題創設的根基，要豐富主體創設的經驗等。^［41］唐恒鈞、張維忠以范希爾理論為依據，選取中美兩國各一版初中幾何教材，比較其中共有的“相似”內容，發現我國教材中的問題情境零散，由此提出要注重教材中問題情境的連續性，來引領學生思維水平的發展。^［42］上述討論反映出，相關的策略主要關注情境與教學內容、學生主體的適配性。

（三） 情境使用（教學）的基本模式

有研究者在多年實踐探索的基礎上，形成了具有顯著成效的情境教學模式。比如，呂傳漢、汪秉彝推動形成了“情境問題”教學體系。^［43］其中，“情境—提問—解決—應用”4個基本環節高度關聯，即情境引導問題的提出，問題可以生成新的情境，而在解決和應用問題的過程中又可以提出新的問題、生成新的情境，以此構成“情境—提問—解決—應用—情境—提問—解決—應用”的教學流程。情境在動態循環、開放延伸的過程中不斷生成和使用，貫穿教學始終。由此，對學生問題提出和解決能力的培育也滲透于教學的全過程中。此外，以李吉林為代表的情境教學法針對易被忽視的態度、情感等因素展開了探索研究，逐步形成了情境教育的理論與操作體系，對數學學科亦產生了重大影響。^［44］

（四） 試題與作業中的情境設計

國內數學試題中情境的研究已引起越來越多的關注。已有研究大多借鑒PISA測評中情境的分類來對中、高考情境化試題進行分析，由此得出關于情境化試題設計或教學實踐的啟發。高中課標強調，在命題中選擇合適的問題情境作為考查數學學科核心素養的重要載體。柯躍海從高考評價體系和數學學科特點入手，將試題情境劃分為六大類，并提出試題情境的創設可以為落實價值引領、素養導向、能力為重、知識為基的高考命題理念提供載體和方法保障。^［45］趙軒等通過對近些年高考全國卷中情境化試題的分析比較，結合試題特征將情境化試題分為六大類，并指出要不斷創新試題形式和內涵，增強試題的開放性和靈活性，以充分發揮區分選拔功能。^［46］上述研究盡管切入角度有所不同，但是都凸顯了情境化試題的目標定位，可以概括為以下兩方面：第一，試題情境與數學核心素養關聯，指向核心素養發展水平的考查；第二，情境化試題的開放性、靈活性和類型的多樣性共同體現著要創設復雜程度不同的情境，從不同層級貫徹數學核心素養的考查。

作業與試題雖有差異，但在內容、形式、功能等諸多方面也存在共性，比如都有診斷和反饋功能。這在一定程度上造成作業的情境設計與試題關聯甚密，大量中、高考試題出現在作業中的現象。“雙減”政策強調“作業布置更加科學合理”，“促進學生全面發展、健康成長”，因此，中小學作業的設計必須堅持全面育人的基本導向。^［47］與情境化試題指向數學核心素養的考查不同，作業作為教學活動的重要環節，其情境設計指向數學核心素養的發展，這與情境在教學中的功能是一致以及連續的。情境究竟如何在數學作業編制中發揮其獨有的價值？數學學科領域具有針對性的設計理念及策略研究仍在不斷發展、完善的過程中。

五、啟示及展望

當前，人們對情境的認識基本已經實現了從“工具觀”“階段論”到“本體觀”“過程論”的跨越，數學教育領域也有越來越多的研究者用情境的視角探索課堂教學、考試評價等問題，數學教育中情境的研究呈現多主題應用的繁榮趨勢。展望未來，數學教育中的情境研究可以從以下幾個層面推進：

首先，關注不同語境下情境的內涵與特征。現有的情境教學模式研究多采用自下而上的方式，即先在實踐中探索，再進行理論層面的歸納總結。這也就解釋了為何數學教育領域對“數學情境”“問題情境”“教學情境”等詞語使用頻繁，而相應的內涵與特征研究很少。然而，隨著情境應用的主題越來越多元化，概念界定的缺失不僅會導致研究者理解上的不一致，更會遮蔽如“教學情境”“試題情境”“情境作業”等詞語之間的關聯。這種關聯反映的是情境在不同的主題中使用時的共性。這種共性往往具有研究價值。例如，情境在課堂教學和課后作業中使用的共性可能對落實“教、學、評一體化”有積極意義。數學教育中，這類研究發展得仍不夠成熟，其開展的前提是“情境作業”的明確界定。

其次，建構作業和試題中情境的操作體系。當前，情境化試題的價值已經被眾多數學教育研究者關注到，并且有不少借鑒PISA、NAEP、TIMSS等國際教育評價項目對試題情境的界定和分類而展開試題命制或評估的探索。作為教師，最關注的還是“怎么做”，即如何設計情境化試題來考查學生的關鍵能力。因此，可以繼續參考PISA等項目將情境具體化和操作化的方法，將情境的要素分解后輔以具體的描述，不斷推進情境化試題操作體系的建立和完善。前文已經提到情境在作業中的價值，而在數學作業中設計情境需要有針對性的原則、理念、策略作為支撐。比如，對于化學學科，呂天恩等明確了情境化作業的含義和設計依據，建構了“4原則、6流程”的高中化學情境化作業設計框架。^［48］

最后，探索情境與智慧教育的融合。隨著新科技革命的來臨，各種新興智能技術逐漸嵌入課堂教學各個環節，未來課堂教學生態將趨向復雜。^［49］情境教學和智慧教育都重視優化環境以促進兒童成長，因此存在著關聯。二者的有機融合將再次帶動教學模式和學習方式的變革，探索適合數學學科的“情境智慧”教育模式就顯得尤為重要了。

參考文獻：

［1］陳碧芬，張維忠，唐恒鈞.“數學教學回歸生活”：回顧與反思［J］.全球教育展望，2012（1）：8692.

［2］王燦明.情境教育四十年的回顧與前瞻［J］.南通大學學報（社會科學版），2020（2）：132140.

［3］呂傳漢，汪秉彝.再論中小學“數學情境與提出問題”的數學學習［J］.數學教育學報，2002（4）：7276.

［4］［20］常磊，鮑建生.情境視角下的數學核心素養［J］.數學教育學報，2017（2）：2428.

［5］［34］［35］黃翔，李開慧.關于數學課程的情境化設計［J］.課程·教材·教法，2006（9）：3943，3943，3943.

［6］呂昌旭，汪秉彝.淺析數學情境的創設［J］.貴州師范大學學報（自然科學版），2002（1）：7881+117.

［7］夏小剛，汪秉彝.數學情境的創設與數學問題的提出［J］.數學教育學報，2003（1）：2932.

［8］［14］任旭，夏小剛.問題情境的創設：基于思維發展的理解［J］.數學教育學報，2017（4）：1518，1518.

［9］許玉梅.淺談數學教學問題情境創設的重要性及原則［J］.教育教學論壇，2015（4）：239240.

［10］周濂.創設數學教學情境 將抽象概念直觀化［J］.中國電化教育，2008（4）：8789.

［11］唐小丹.數學問題情境創設的有效性探討［J］.教學與管理，2011（27）：133134.

［12］邱家寰.探析高中數學中如何設置問題情境啟發學生［J］.教育教學論壇，2012（24）：8485.

［13］周先榮，張國棣.關于問題情境數學性的思考［J］.數學通報， 2008（5）：2224.

［15］張廣斌.教學情境的結構與類型研究——結構功能主義視角［J］.教育理論與實踐，2010（13）：5760.

［16］張輝蓉，朱德全.走出教學情境創設的誤區［J］.西南大學學報（社會科學版），2007（5）：126129.

［17］李鵬鴿.創設教學情境的有關問題研究［J］.教學與管理，2010（36）：121122.

［18］［44］李吉林.情境教育的獨特優勢及其建構［J］.教育研究，2009（3）：5259，5259.

［19］呂傳漢，汪秉彝.論中小學“數學情境與提出問題”的教學［J］.數學教育學報，2006（2）：7479.

［21］史寧中，郭民.中學數學證明的教育價值——數學教育熱點問題系列訪談之四［J］.課程·教材·教法，2007（7）：2327.

［22］W.Blum， P.L.Galbraith， H.W.Henn， et al. Modelling and applications in mathematics education［M］.New York： Springer： 45.

［23］周文葉，陳銘洲.指向核心素養的表現性評價［J］.課程·教材·教法，2017（9）：3643.

［24］王小明.表現性評價：一種高級學習的評價方法［J］.全球教育展望，2003（11）：4751.

［25］李新民.非智力因素對教學過程的影響及其定量分析［J］.教育理論與實踐，2006（20）：3638.

［26］崔進平.非智力型數學差生轉化案例［J］.數學教育學報，1999（1）：2528.

［27］顏中玉.非智力因素對高師數學學習影響的調查［J］.數學教育學報，2001（2）：4447.

［28］王光明，刁穎.高效數學學習的心理特征研究［J］.數學教育學報，2009（5）：5156.

［29］康玥媛，張楠，王光明，等.高效率數學學習高中生數學成績的影響路徑［J］.心理與行為研究，2016（3）：352359.

［30］李健.初中數學教科書中現實問題情境設置的實證研究——基于中外九版初中數學教科書的縱向與橫向比較［D］.天津：天津師范大學，2019：5152.

［31］龐坤，李明振，宋乃慶.GX實驗是實施數學素質教育的成功范例［J］.西南大學學報（自然科學版），2008（2）：161164.

［32］OECD. PISA2015 Results（Volume Ⅴ）： Collaborative Problem Solving［M］.Paris： OECD Publishing， 2017： 4650.

［33］王薇.指向問題解決能力發展的學習活動模型研究——基于情境學習理論的分析框架［J］.教育學術月刊，2020（6）：8895.

［36］李月勝.去情境，從生活數學走向符號世界［J］.上海教育科研，2019（12）：6972+42.

［37］李健，李海東.數學教科書中設置問題情境的作用與原則［J］.基礎教育課程，2020（17）：5966.

［38］吳黎貞.小學數學情境教學的有效創設［J］.現代教育科學，2009（12）：9293.

［39］吳華，馬東艷.用多媒體技術創設數學教學的多元情境［J］.中國電化教育，2007（6）：8083.

［40］劉允忠.新課標背景下的高中數學情境創設策略的探討［J］.數學通報，2006（1）：1820.

［41］張秀花.小學數學教學中有效問題情境的創設［J］.教育理論與實踐，2015（35）：5658.

［42］唐恒鈞，張維忠.中美初中幾何教材“相似”內容的比較［J］.數學教育學報，2005（4）：5558.

［43］呂傳漢，汪秉彝.中小學“數學情境與提出問題”教學的理論基礎及實施策略［J］.貴州師范大學學報（自然科學版），2007（1）：95100.

［45］柯躍海.高考數學試題情境的創設實踐［J］.中國考試，2020（6）：19.

［46］趙軒，任子朝，翟嘉祺.高考數學科情境化試題設計研究［J］.數學通報，2021（12）：13+66.

［47］楊清.“雙減”背景下中小學作業改進研究［J］.中國教育學刊，2021（12）：610.

［48］呂天恩，占小紅，林美鳳.高中化學情境化作業設計研究——以“烴的衍生物”單元作業為例［J］.化學教育（中英文），2022（5）：6267.

［49］王一巖，鄭永和.面向智慧課堂的教育情境感知：價值定位、特征模型與實踐框架［J］.電化教育研究，2021（11）：8491.

（鄭蓉蓉，浙江師范大學教育學院。主要研究方向：數學課程與教學。

蔣逸卿，浙江師范大學教育學院。主要研究方向：數學課程與教學。

唐恒鈞，浙江師范大學教育學院，博士后，教授，博士生導師。主要研究方向：數學課程與教學。）