新工科背景下“復變函數與積分變換”教學改革探索

［摘 要］ 新工科背景下對人才培養提出了新的要求，其內涵是以立德樹人為引領，培養多元化、創新型工程人才。新工科教育理念突出了數學理論和方法對工科專業的支撐作用。在新工科的教育理念和背景下，針對當前“復變函數與積分變換”教學中存在的不足，從課程思政、教學內容、教學方法、教學模式、考核模式等方面進行了改革，以提高學生的學習興趣、提高教學效果，培養符合新工科要求的具有高級思維能力、實際應用能力及正確價值觀的創新型人才。

［關鍵詞］ 新工科；教學改革；課程思政；可視化教學

［基金項目］ 2022年度山東省精品示范課“數學物理方程”（16202210003）

［作者簡介］ 牟海寧（1979—），女，山東棲霞人，理學博士，中國石油大學（華東）理學院講師，主要從事數值計算和偏微分方程研究。

［中圖分類號］ G642.0 ［文獻標識碼］ A ［文章編號］ 1674-9324（2024）26-0045-04 ［收稿日期］ 2023-09-28

引言

在新工科背景下，各高校需秉承立德樹人根本任務，以培養應用型、創新型人才為目標，積極開展教育教學改革［1-2］。“復變函數與積分變換”是高等院校中許多工科專業的重要數學基礎課。復變函數論在流體力學、電磁學等領域有著廣泛應用，而積分變換理論在信號處理、自動控制、圖形圖像處理、地質勘探等工程技術領域有著重要應用［3］。學習此課程能夠培養學生的數學素養和應用能力，培養學生分析問題、解決問題的能力。“復變函數與積分變換”內容主要包括：復數與復變函數、解析函數、復變函數積分、級數、留數及其應用、共形映射、傅里葉積分變換和拉普拉斯變換等，內容比較抽象、理論性和實用性強，很多學生認為課程比較難學，有畏難心理。為提高學生的學習興趣，提升教學效果，培養學生的創新思維能力，我們從課程思政、教學內容、教學方法、教學模式以及考核模式等方面進行了教學改革探索。

一、課程教學中存在的問題

根據十多年的教學經驗以及調查研究發現，“復變函數與積分變換”教學中存在以下問題［4］。

1.課程思政教育不足。教師對思政的認識和重視不足。多數教師只注重傳授專業知識而忽視了思政教育。“復變函數與積分變換”課程中蘊含著豐富的思政元素，但教學過程中缺少思政教育，未能充分發揮其育人功能。

2.教學內容與專業結合不夠緊密，缺乏前沿性知識。在傳統教學中，面對不同專業、不同層次的學生，教學內容是統一的，學生只能被動接受教學內容和進度，導致學生對課程的學習興趣打折扣。

3.教學模式單一。以教師為主體的灌輸式教學方式無法較好地激發學生的學習主動性和積極性，不能有效地追蹤到學生的學習效果。如何讓學生成為學習的主體，激發其學習興趣和主動性是急需解決的關鍵問題。

4.教學手段和教學方法單一。由于復變函數理論的抽象性特點，如何將傳統的板書教學與PPT教學兩者有機結合起來是關鍵，引入可視化教學，將抽象問題直觀化。

5.考核模式單一。傳統的考核方式是平時作業+期末考試，缺少對學生的過程化考核，無法對學生的學習情況進行持續追蹤和監督，缺乏教育評價的診斷和改進功能，導致部分學生學習效果欠佳。

二、教學改革措施

新工科的教育背景下，要求在教學中以“學生為中心”，以專業需求為導向，培養具有高級思維能力、創新能力的德才兼備的可持續性發展的人才。針對上述提出的問題及新工科的教育理念，采取以下幾個改革措施。

（一）加強思政建設

充分挖掘“復變函數與積分變換”課程中的思政元素，將其融入教學過程中，激發學生的學習熱情，提高學生的探索精神，培養學生的科學素養。例如，第一堂課介紹復變函數的發展歷史及其在實際工程領域中的應用時，向學生介紹柯西、黎曼和魏爾斯特拉斯等科學家對復變函數領域做出的貢獻，使學生認識到復變函數論發展至今是一代代科學家艱苦努力取得的成果，以此激勵學生不畏艱苦、勇于追求科學真理。

“復變函數與積分變換”是“高等數學”的后續課程，許多定理和結論都是“高等數學”在實數域中的推廣和發展，但許多結論和實函數的結論不同，甚至相悖。如在復數域中，負數可以開平方根并且任何一個非零負數開n次方根有且僅有n個不同的根等；在復變函數中，指數函數ez是周期函數，三角函數sin z和cos z為無界函數。因此，在教學中引入類比教學法，引導學生找到相關結論的異同，引導學生用發展的思維思考問題，培養學生的探究精神和嚴謹的科學精神。

柯西積分公式和高階導數公式說明對于解析函數來說，區域內部的函數值完全可由邊界上的積分值來確定，即“邊界決定內部”的數學思想，這彰顯了解析函數局部反映整體的性質，由此可引導學生在學習時要善于發現、總結數學規律，探究數學思想，有助于培養良好的數學思維。

在講解洛朗級數時，向學生介紹科學家洛朗理論結合實際的能力非常強，讓學生學習洛朗理論應用于實際的能力。同時，教師要搜集、提煉復變函數與積分變換知識在實際工程中的應用實例，建立相關案例庫，教學時有意識地培養學生的理論聯系實際的能力和理論應用于實際的能力。

總之，我們應將思政教育貫穿教學始終，對學生進行價值引領，但要注意思政教育應與課程內容有效融合，不能生搬硬套。

（二）教學內容改革

1.教學內容與專業緊密結合。搜集并建立專業案例庫，在教學內容上選擇與學生專業相結合的案例，提高學生的學習興趣。例如，講解解析函數在實際中的應用時，對力學專業的學生，引入解析函數在平面流體場中的應用案例；對物理專業的學生，引入解析函數在平面靜電場中的應用案例。講解拉普拉斯積分變換時，對電信專業的學生引入信號處理方面的應用實例；講解傅里葉積分變換時，對光電專業的學生引入光學方面的應用實例等。

2.教學內容與前沿知識相結合。在本課程教學中，存在學生的基礎知識水平有較大差異的情況。部分學生由于“高等數學”基礎較弱，學起來吃力，而基礎好的學生知識接受能力強，渴望新知識。因此，在注重基礎知識和基本技能的前提下，要適當引入高階性、前沿性的知識。這要求教師要及時增加知識儲備，及時了解復變函數領域和積分變換領域的前沿進展。在教學過程中適當引入前沿知識，提高教學內容的前沿性和高階性，滿足不同層次學生的學習需求，真正做到以尊重學生個性化發展為前提的分層次教學。此外，可在每一章引入相關的拓展知識問題，組織學生進行分組研討并匯報，培養學生的創新思維和解決問題的能力以及團隊合作能力。

（三）教學模式改革

在教學過程中始終遵循以“學生為中心”的教育理念，讓學生成為學習的主體，采取線上線下混合教學模式［5］，充分發揮學生的學習積極性。

線上線下混合教學模式是學生線上自學和傳統線下教學相結合的新型教學模式，充分利用信息技術和網絡資源，借助于慕課、愛課程、智慧樹等平臺進行輔助教學。目前所采取的線上線下混合教學模式是以“線下為主，線上為輔”。對于線上自學課，教師將學習任務在平臺上提前布置給學生，學生學習線上教學視頻、教學課件等，并在規定時間內完成相關測試。為此，教師需要根據課程內容，制訂好課程計劃。

1.對教學內容和教學課時進行劃分。根據內容難易程度及與前后的關聯程度，將課程內容分為學生線上自學內容和線下講授內容兩部分。一般線上課時占總課時的20%左右。

2.制定自學導學單。以學習目標、問題引入、學習內容、學習要求、作業、思考拓展、思政元素為模塊做成導學單，引導學生進行自學。在智慧樹等平臺向學生布置學習任務，讓學生按照導學單的要求進行自學，并完成相關作業和測試。

3.布置測試。每次自學都緊跟一次線上測試以檢驗學生的學習效果。課程組教師提前做好題庫，按知識點將試題分類，借助于智慧樹平臺將測試布置給學生。試題與學習內容緊密關聯，按難易程度分類，每次測試都隨機組卷，打亂題目順序，并讓學生在限定時間內完成。

線上自學過程中，學生可以隨時通過QQ、微信等及時與教師交流，教師要及時為學生答疑解惑。自學后緊跟的線上測試可以反饋學生的學習情況。這樣線下授課時，教師可以有針對性地進行教學，提高教學效果，線下教學時可利用信息技術與學生進行有效互動。例如，課中充分利用雨課堂，講課過程中針對重要知識點及時插入雨課堂測試，隨時掌握學生學習情況。對大部分學生掌握欠佳的知識點進行再次講解，以保證教學效果。這樣既可以調動學生的學習積極性，又實現了對學生的過程化考核。

自學視頻可以選取慕課、愛課程等網站的精品課程視頻，課程組教師也可錄制微課視頻。將教學內容系統分類后進行“碎片化”處理，錄制時長較短的微課視頻，學生可以隨時隨地學習。在每個視頻中都加入彈題，學生在學習完某部分知識后，通過做彈題理解、檢測學習重點和學習效果。對于難度較大、比較抽象的問題，還可錄制答疑視頻，有需要的學生可以觀看解惑。通過錄制拓展視頻，滿足學生的學習成長需求。線上線下混合式教學模式可以充分調動學生的學習積極性和主動性，培養學生的自學能力和科學探索能力。

（四）教學手段和教學方法改革

1.板書與PPT相結合。在線下教學時，應將板書教學和PPT教學有機結合，既可以節省時間、豐富教學內容、增加課堂的信息量，又可以保證課堂教學有效性。例如，涉及定理證明時，應結合啟發式教學方法，進行板書講解，便于學生思路跟進，有助于培養學生的邏輯思維能力；講述函數的性質時，借助于PPT演示，有助于學生的直觀理解。

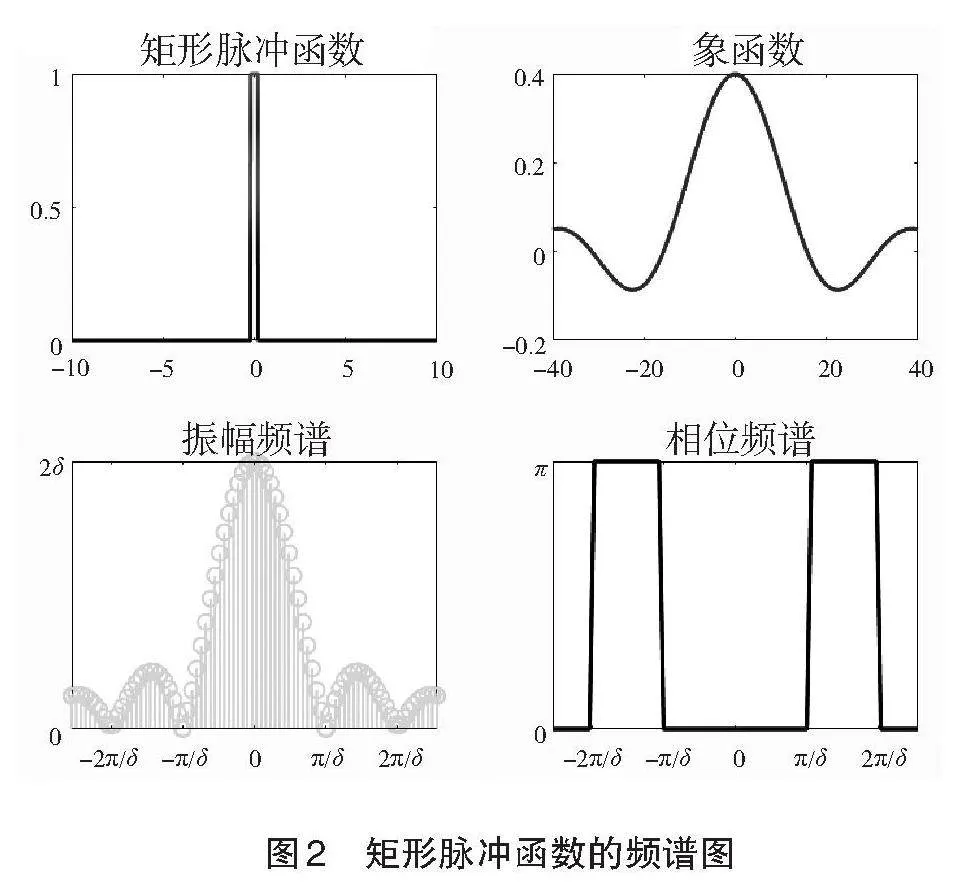
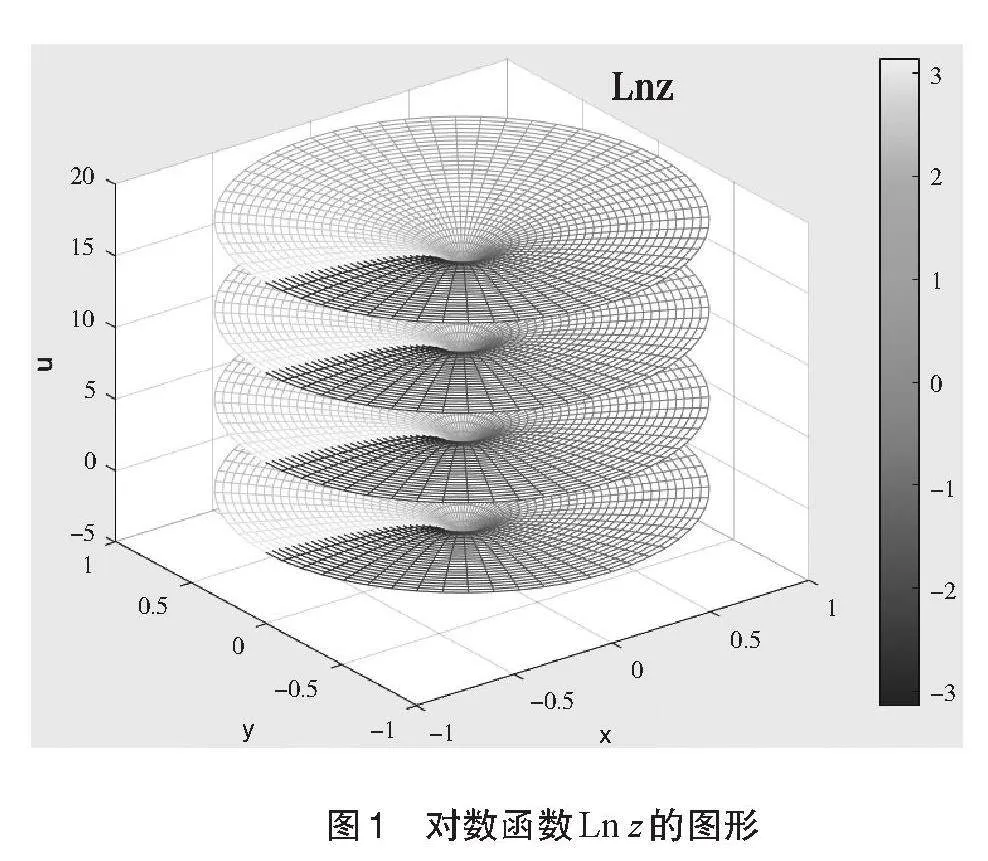
2.可視化教學。由于“復變函數與積分變換”課程的理論性強、內容比較抽象，很多學生感到乏味、難以理解。在教學過程中引入可視化教學手段，可將抽象的問題直觀化，有助于學生對內容和內在規律進行分析與理解。例如，在講解對數函數時借助于其可視化圖形，可看出其多值性，以及各個值的實部、虛部之間的關系。如圖1所示，畫出的是Ln z=ln |z|+iarg z+2kπi在k=0，1，2，3時的圖形。從圖1可以看出，對數函數Ln z的四個值的實部值（豎軸代表函數的實部值）相等，而虛部值（顏色代表函數的虛部值）之間相差一個常數。再例如，講解傅里葉積分變換時，利用可視化圖形有助于理解象函數的物理意義。如圖2所示，繪制的是矩形脈沖函數的傅氏變換的頻譜圖。由圖2可理解象函數的模代表了各個頻率成分的函數在信號中所占的比重。

可視化教學可以使教學過程生動化、形象化、直觀化，有助于學生理解抽象知識，能夠提高學生的學習興趣。

（五）考核方式改革

基于新工科內涵，需建立能夠全面評價學生的綜合能力的多元化考核模式。由于本課程實行線上線下混合式教學，增強了過程化考核，使得考核評價更有時效性和全面性。本課程的考核采用多維度的評價方式，評價分為以下幾個模塊。

1.課程小論文。讓學生撰寫基于本課程且與專業相關的課程論文，并組織答辯。論文評分要素有：（1）選題情況（與本課程的相關度、難易程度）；（2）問題解決情況（模型建立、求解方法、求解步驟、程序實現）；（3）總結（結果分析與探討）；（4）論文書寫情況（邏輯性、規范性、充實性）；（5）答辯情況（PPT講解、語言表達、回答問題）。從深度和廣度上對學生進行評價，有助于培養學生的創新能力。

2.過程化考核。包括平時作業、課堂表現，以及每次自學測試等，過程化考核貫穿整個學習過程，有助于對學生的學習情況進行診斷和改進。

3.期末考試。期末考試試題將基礎理論知識測試和實際能力測試并重，以培養學生解決實際問題的能力。

結語

筆者將上述改革措施應用于2020級和2021級石油工程專業、電子通信專業、地學專業，進行了兩個學期的“復變函數與積分變換”課程教學試驗，發現與之前相比，學生的學習積極性有了很大提高，也取得了較好的教學效果。經過調查，學生對教學的滿意度也有所提高。新工科建設對教師的教學提出了新的要求，我們必須不斷深化改革教學內容和教學方式，提高教學質量。

參考文獻

［1］楊旭.新工科背景下基于混合式教學的編譯原理課程教學改革探析［J］.計算機產品與流通，2019（12）：224-225.

［2］牛英春，張天宇.思政元素在《復變函數論》混合課改中的應用［J］.當代教育實踐與教學研究，2019（6）：204-205.

［3］張高民，崔儉春，呂鋒，等.復變函數與積分變換［M］.青島：中國石油大學出版社，2022：32-38.

［4］龐洪博.復變函數課程思政的探索與實踐［J］.遼寧工業大學學報，2022，24（6）：132-134.

［5］肖立勇，尹躍.基于混合式教學模式下的大學物理實驗教學改革和應用［J］.物理通報，2020（4）：84-88.

Exploration on Teaching Reform of Complex Variable Function and Integral Transform under the Background of Emerging Engineering Education

MOU Hai-ning

（College of Science， China University of Petroleum （East China）， Qingdao， Shandong 266580， China）

Abstract： Under the background of emerging engineering education， new requirements are put forward for talent training. Its connotation is to cultivate diversified and innovative talents guided by moral education. The emerging engineering education concept highlights the supporting role of mathematical theories and methods in engineering majors. Under the educational concept and background of new engineering， aiming at the shortcomings in the current teaching of complex variable function and integral transform， the reform is carried out from the aspects of curriculum ideology and politics， teaching content， teaching method， teaching mode and assessment mode， so as to improve students’ interest in learning， improve teaching effect， and cultivate innovative talents with advanced thinking ability， practical application ability and correct values in line with the requirements of new engineering.

Key words： emerging engineering education; teaching reform; curriculum ideology and politics; visual teaching