新課標下立體幾何教學的分析與探討

底軍艷

摘 要：新課標改革對高中數學教學提出了新的要求，在此背景下，作為培養學生邏輯推理能力、空間想象能力、幾何直觀能力的載體，立體幾何在高中數學教學中顯得至關重要。如何提高立體幾何課堂教學的效果，通過怎樣的手段實現教學效率最大化成為了新課標改革中備受關注的問題。本文中，筆者就對立體幾何教學的現狀、教學目標以及方法策略進行分析和探討。

關鍵詞：新課標 立體幾何教學 現狀分析 策略探討

中圖分類號：G633.6 文獻標識碼：A 文章編號：1673-9795（2014）02（c）-0056-01

作為高中數學課程中唯一一門對學生空間想象能力進行培養的課程，立體幾何在新課程改革中是作為重點和熱點內容被看待的。根據新課標對高中數學改革的內容來看，立體幾何的教育功能主要可以從知識方面、數學能力方面以及情感態度方面進行分析。第一個知識方面，能夠幫助學生掌握基本的關于立體圖形的性質及概念；第二個數學能力方面，能夠實現對學生幾何直觀能力、空間想象能力以及邏輯推理能力的形成和提升；第三個情感態度價值觀方面，可以幫助學生提升對客觀規律的思維能力。由此可見，在新課標改革下對立體幾何教學的價值進行分析和探討是具有重要意義的，是需要被廣大教育者關注的一個重要問題。

1 立體幾何研究現狀

高中教學大綱中的立體幾何知識具有抽象程度高、空間性強等特點，學生的積極性和容易受到打擊，就算生硬地學完，過了一段時間往往也會幾乎忘光。到了高三復習的時候，很多學生都有上新課這樣的感覺，造成這種現象的根本原因就是學生缺乏系統的立體空間概念，邏輯推理論證能力沒有得到鍛煉。造成這一現象的因素有很多，第一，學生缺乏對數學語言的深入全面理解，空間想象力不夠好。第二，老師在實際課堂教學中往往認為只要教會學生解題的方法就行了，對學生數學語言的培養不夠重視。第三，關于教材內容編排方面，針對提高學生數學語言能力方面涉及地較少，也缺乏足夠的練習。對我們的立體幾何教學中存在問題進行分析后，我們就需要針對存在的問題進行改進，探討更合理、科學的立體幾何教學策略[1]。

2 新課標立體幾何教學要求

2.1 重視直觀感知，構建相關概念

在立體幾何中，定理是指經過嚴格邏輯論證后的命題，并且我們需要承認只有通過直覺理解，學生才能真正想通領悟并接受。眾所周知，創新往往發端于直覺，立體幾何作為一種形象、直觀的數學模型，其對提高學生創新精神、發展學生直覺能力上具有不可低估的價值[2]。學生在立體幾何學習過程中，通過觀察、操作、作圖、設計、猜想等方式進行幾何圖形性質研究的過程中，往往能得到視覺和心理上的愉悅。這樣就給學生提供了學習積極性，進而增強他們的探究好奇心，從而激發出潛在的創造力，最終就成為了我們所追求的創新意識。

2.2 注重培養學生抽象概括能力

在數學學習及知識理解中，直觀固然重要，但直觀只是一種手段，并不是目的。進行幾何教育的目的不應該僅僅只是給學生灌輸相關的圖形理論知識，而更應該注重在過程中對學生各方面能力的培養，例如引導學生通過實物模型學會怎樣將自然語言轉化為符號語言和數字語言，又例如通過教導他們垂直關系、平行關系，讓他們學會使用數學語言表達幾何對象的位置關系。在這樣的基礎上，當學生的感性認識得到一定的積累后，就需要在適當的實際引導他們獨立進行抽象概括、數學語言描述以及動手畫圖等活動。

3 立體幾何教學策略研究

3.1 創設操作性問題情境

新課標教學要求強調，要重視教學過程中的問題情境創設，即幫助學生經歷立體幾何定理的形成過程中，加深他們對立體幾何知識的理解、增強情感體驗進而培養其空間想象力。在教學過程中創設動手操作問題，不僅能夠激發學生的好奇心和學習興趣，更能激發學生的聯想思維，大大降低學生在學習過程中的排斥感和恐懼感。

例如，在進行凸多面知識點的教學中，教師們可以引導學生去發現周圍生活中的各種多面體，而不是像傳統教學一樣，拿著各種幾何體的模型在講臺上展示給大家看[2]。教師可以將學生進行合理分組，然后為每小組提供一個正方體框架，這些正方體的六個面對角線是用橡皮筋連接的，然后啟發學生通過拉動皮筋構造出各種其他的多面體。這樣現實的問題情境，能夠讓學生真正參與到學習中來，身臨其中去感受和經歷概念以及公式的形成、發展過程，進而加深他們對知識的理解和記憶。

3.2 培養學生靈活解題的能力

一般來說在解題中如果遇到向量坐標運算思維量較少、運算技巧較低等情況時，教師可以指導學生采用更便捷的解題方法，如建立合適的坐標系，并準確寫出相關點的坐標。

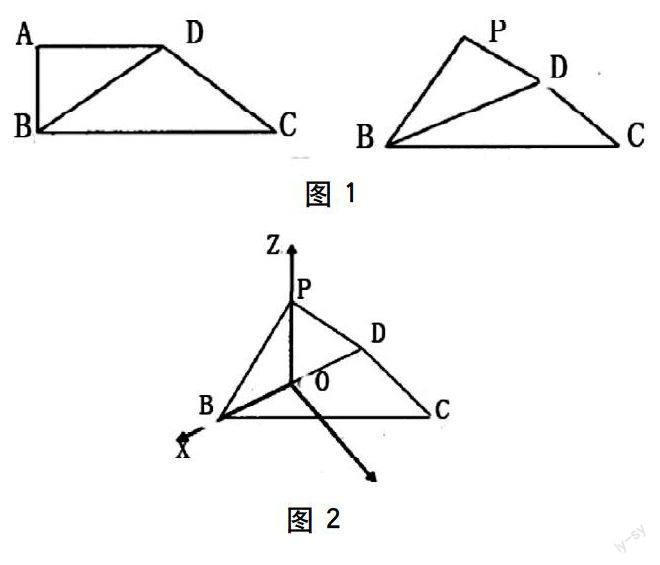
例如，如圖1，已知四邊形ABCD中，AD//BC，AD=AB=1，∠BCD=45°，∠BAD：90°，將△ABD沿BD折到如圖1PBD的位置，使面PBD垂直于面BCD。（1）求證CD垂直于PB。（2）求二面角P—BC—D的余弦。（3）求點D到平面PBC的距離。

在上題中，由于圖形中缺乏顯性的空間直角坐標系的模型，我們可以利用綜合法對線面位置關系進行分析，建立空間直角坐標系實現靈活解題，如圖2，以BD中點O作為原點建立空間直角坐標系。

3.3 培養學生幾何直觀能力

一般我們所說的幾何直觀能力包括以下幾點，分別為直觀洞察能力、空間想象力以及圖形語言思考問題的能力。受制于傳統的幾何教學常規作圖工具，所有的圖形都是靜態的，學習過程時冷冰、死板的。針對這一問題，我們可以借助于現代信息技術，通過逼真而具體的動態演示將靜態、抽象的圖像展示給學生，幫助他們建立豐富的感性知識，進而發現立體幾何問題的本質，達到教學的根本目的。

例如，在對定理：“三棱錐的體積等于它的底面積S與高h的乘積的三分之一”進行教學時，我們可以利用《幾何畫板》幫助學生進行探究學習，為學生提供動態的畫面，誘發學生的聯想能力，進而實現對他們類比能力的培養和提高。

參考文獻

[1] 王小紅.高中數學實驗教學創設的幾種途徑[J].中學數學教學參考，2011（9）：23-25.

[2] 趙艷霞.新課標下立體幾何教學初探[J].課改前沿，2010（5）：64-66.