新時(shí)期熱沖壓成形技術(shù)的構(gòu)建探究
劉相根

摘 ? 要:熱沖壓成形技術(shù)是一種常見的零件加工方式,尤其在汽車工業(yè)中應(yīng)用最為普遍。本文介紹了熱沖壓成形技術(shù)的基本原理,分析了溫度、時(shí)間、成形速度以及冷卻速度對(duì)沖壓成形的影響。并以汽車零部件加工為主要研究對(duì)象,通過(guò)熱沖壓技術(shù)獲取輕量化高強(qiáng)度的成形件,通過(guò)檢測(cè)成形件微觀組織為馬氏體,抗拉強(qiáng)度為1500MPa滿足汽車生產(chǎn)要求。
關(guān)鍵詞:新時(shí)期 ?熱成形 ?沖壓
中圖分類號(hào):TG385 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻(xiàn)標(biāo)識(shí)碼:A ? ? ? ? ? ? ? ? ? ? ? 文章編號(hào):1674-098X(2020)02(b)-0060-02
熱沖壓成形技術(shù)是一種常見的零件加工方式,尤其在汽車工業(yè)中應(yīng)用最為普遍。將材料先加熱至奧氏體化狀態(tài),該狀態(tài)下鋼板材料的塑性較好,強(qiáng)度低,并且具有一定的韌性,然后使用沖壓機(jī)在模具中進(jìn)行沖壓并淬火,獲得相應(yīng)形狀的高強(qiáng)度金屬零件。通過(guò)熱沖壓成形技術(shù)獲取高強(qiáng)度的沖壓件來(lái)代替?zhèn)鹘y(tǒng)的厚鋼板,不但可以有效降低零部件自身的重量,而且能大幅度地提升抗拉強(qiáng)度,廣泛應(yīng)用于汽車保險(xiǎn)杠、AB柱、車頂側(cè)梁的制造中,下面就對(duì)新時(shí)期熱沖壓成形技術(shù)的構(gòu)建進(jìn)行深入分析。
1 ?熱沖壓技術(shù)原理
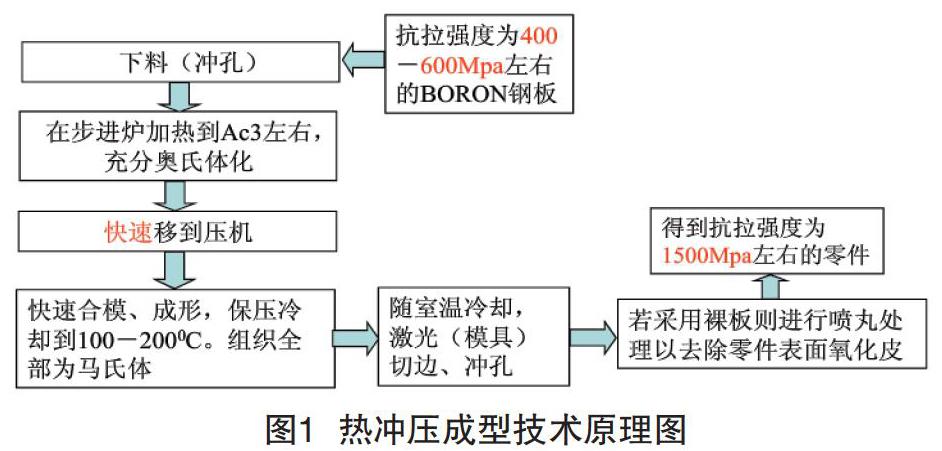
熱沖壓技術(shù)是一種將鋼板材料加熱至奧氏體形態(tài)下,快速進(jìn)行沖壓成形,并且通過(guò)模具對(duì)零件進(jìn)行淬火冷卻,獲得強(qiáng)度為1500MPa左右的馬氏體成形件。可以說(shuō)熱沖壓技術(shù)是將鋼板材料由奧氏體向馬氏體轉(zhuǎn)化的過(guò)程。奧氏體(Austenite)是鋼鐵的一種層片狀的顯微組織,該狀態(tài)下的鋼板材料?-Fe中固溶少量碳的無(wú)磁性固溶體,因此也稱為沃斯田鐵或者?-Fe。馬氏體(Martensite)是黑色金屬材料的一種組織名稱,是碳在α-Fe中的過(guò)飽和固溶體。馬氏體和奧氏體的不同在于,馬氏體是體心正方結(jié)構(gòu),奧氏體是面心立方結(jié)構(gòu)。奧氏體向馬氏體轉(zhuǎn)變僅需很少的能量,因?yàn)檫@種轉(zhuǎn)變是無(wú)擴(kuò)散位移型的,僅僅是迅速和微小的原子重排。馬氏體的密度低于奧氏體,所以轉(zhuǎn)變后體積會(huì)膨脹。相對(duì)于轉(zhuǎn)變帶來(lái)的體積改變,這種變化引起的切應(yīng)力、拉應(yīng)力更需要重視。熱沖壓成形技術(shù)的原理如圖1所示。
熱沖壓成形技術(shù)可以分直接沖壓和間接沖壓兩種形式,其中直接沖壓是將鋼板材料加熱至奧氏體后,直接傳送至模具上沖壓,模具表面有冷卻通道,可以在鋼板材料沖壓的過(guò)程中進(jìn)行淬火冷卻,獲得馬氏體成形件。間接沖壓則是鋼板材料先進(jìn)行冷沖壓,然后再加熱成奧氏體進(jìn)行淬火和校準(zhǔn),確保成形材料強(qiáng)度達(dá)到1500MPa的馬氏體。
2 ?熱沖壓技術(shù)工藝設(shè)計(jì)
熱沖壓成形技術(shù)使用的設(shè)備包括:加熱爐、上下料裝置、沖壓機(jī)、模具、切邊和沖孔設(shè)備。下面就對(duì)熱沖壓成形技術(shù)的工藝設(shè)計(jì)和特點(diǎn)進(jìn)行詳細(xì)分析。
2.1 材料加熱
加熱爐是熱沖壓成形技術(shù)的關(guān)鍵設(shè)備,尤其是在汽車工業(yè)自動(dòng)化生產(chǎn)線上,加熱爐具有自動(dòng)進(jìn)料和出料功能,并且有自動(dòng)溫控裝置,實(shí)現(xiàn)在設(shè)定時(shí)間內(nèi)確保鋼板材料完成奧氏體的轉(zhuǎn)化。
2.2 上下料過(guò)程
上下料裝置主要是通過(guò)機(jī)械手臂將奧氏體材料傳送至模具進(jìn)行沖壓,上下料時(shí)需要平穩(wěn)抓取鋼板,同時(shí)減小夾持點(diǎn)鋼板溫度的變化,因此,采用高速機(jī)械手臂最大限度地縮短上下料的時(shí)間,這對(duì)于降低生成成本,具有十分重要作用。
2.3 沖壓
沖壓機(jī)直接對(duì)奧氏體材料機(jī)械能沖壓,考慮到鋼板材料的熱脹冷縮效應(yīng),需要有效的補(bǔ)償設(shè)計(jì),模具內(nèi)有冷卻回路,具備淬火冷卻功能。考慮到熱沖壓是重新加熱到奧氏體區(qū)的過(guò)程,為了避免和減少加熱過(guò)程對(duì)材料造成的氧化,需要使用鍍層板,提高鍍層的結(jié)合力,防止加熱和成形過(guò)程中的剝落。鍍層板熱沖壓過(guò)程無(wú)氧化皮,減少了噴丸處理的過(guò)程,零件耐腐蝕性能高、不易生銹,但是制造工藝復(fù)雜,成本相對(duì)較高。
2.4 切邊和沖孔
切邊和沖孔是對(duì)沖壓成形件進(jìn)行二次加工,由于成形件強(qiáng)度較高,常采用激光切割進(jìn)行切邊和沖孔。
3 ?熱沖壓技術(shù)應(yīng)用
現(xiàn)階段,中國(guó)寶鋼集團(tuán)是國(guó)內(nèi)唯一熱沖壓鋼供應(yīng)商。使用硼鋼板B1500HS,化學(xué)成分如表1所示。通過(guò)熱沖壓技術(shù)制造汽車零部件,提升材料抗沖擊性能的同時(shí)提升汽車的安全性能和燃油經(jīng)濟(jì)性。下面將通過(guò)實(shí)驗(yàn)驗(yàn)證熱沖壓成形技術(shù)的實(shí)際效果:
實(shí)驗(yàn)過(guò)程中,首先將硼合金鋼板送至加熱爐內(nèi)加熱至900℃,并且保溫5min,確保材料完成奧氏體形態(tài)轉(zhuǎn)變,此次使用的是帶Al-Si鍍層鋼板,防止鋼板材料在加熱過(guò)程中發(fā)生氧化。待鋼板材料完全成為奧氏體形態(tài)后,啟動(dòng)高速機(jī)械臂迅速將材料放入帶有冷卻裝置的沖壓模具上,迅速啟動(dòng)液壓沖壓機(jī)實(shí)現(xiàn)沖壓成形,模具完全閉合后保持10s,確保模具內(nèi)的鋼板充分淬火冷卻,從而實(shí)現(xiàn)鋼板材料由奧氏體向馬氏體的轉(zhuǎn)變。
通過(guò)常溫和高溫狀態(tài)對(duì)材料的單向拉伸進(jìn)行實(shí)驗(yàn),獲取鋼板材料的基本力學(xué)性能數(shù)據(jù)。在室溫條件下,即溫度10℃~50℃時(shí)對(duì)熱沖壓成形沒有明顯影響,保壓時(shí)間為155~260s,冷卻速度一般為21℃/s,沖壓模具自帶淬火冷卻功能,淬火后材料溫度為200℃,冷卻水臨界值為0.7m/s。對(duì)成形件進(jìn)行微觀組織分析,可以得到該成形件的屈服強(qiáng)度可達(dá)1036MPa,抗拉伸強(qiáng)度可達(dá)1547MPa。通過(guò)實(shí)驗(yàn)驗(yàn)證熱沖壓成形件的回彈,壓邊力、凹模圓角半徑和模具溫度對(duì)熱成形下的回彈有較大影響,壓邊力越大,模具溫度越高,凹模圓角半徑越小,回彈量越小,同時(shí)冷卻速率不一致造成的熱效應(yīng)對(duì)回彈也有一定影響。
4 ?結(jié)語(yǔ)
綜上所述,熱沖壓成形技術(shù)是汽車工業(yè)中常用的零部件加工技術(shù),通過(guò)熱沖壓制造的成形件具有強(qiáng)度高、質(zhì)量輕等特點(diǎn)。本文通過(guò)分析熱沖壓成形技術(shù)的基本原理及工藝特點(diǎn),通過(guò)汽車工業(yè)生產(chǎn)的實(shí)際應(yīng)用,驗(yàn)證了熱沖壓成形件強(qiáng)度可達(dá)1000MPa、抗拉強(qiáng)度可達(dá)1500MPa,為理想狀態(tài)下的馬氏體結(jié)構(gòu)。由此可見,熱沖壓成形技術(shù)可以很好的滿足新時(shí)期汽車工業(yè)對(duì)材料輕量化、高強(qiáng)度的技術(shù)要求,具有非常廣闊的應(yīng)用前景。
參考文獻(xiàn)
[1] 張宜生,王子健,王梁.高強(qiáng)鋼熱沖壓成形工藝及裝備進(jìn)展[J].塑性工程學(xué)報(bào),2018(5):98.
[2] 黃大鵬,楊國(guó)慶,張梅,等.熱沖壓成形技術(shù)及其新進(jìn)展[J].上海金屬,2017(5):145.
[3] 苑雪雷,葉明禮,尹詩(shī)嶄.淺談熱沖壓成形技術(shù)[J].模具制造,2016(6):95.
 科技創(chuàng)新導(dǎo)報(bào)2020年5期
科技創(chuàng)新導(dǎo)報(bào)2020年5期
- 科技創(chuàng)新導(dǎo)報(bào)的其它文章
- 高校“雙創(chuàng)”人才培養(yǎng)體系中融入創(chuàng)客教育培養(yǎng)實(shí)踐研究
- 讓學(xué)生走上講臺(tái)的生物化學(xué)實(shí)驗(yàn)的教學(xué)實(shí)踐
- 專利對(duì)于制造型企業(yè)市場(chǎng)競(jìng)爭(zhēng)影響力的研究與分析
- 統(tǒng)計(jì)基層基礎(chǔ)規(guī)范化建設(shè)分析
- EEM和PARAPAC對(duì)地表水中DOM分析新進(jìn)展
- 基于中國(guó)傳統(tǒng)文化背景下的現(xiàn)代產(chǎn)品設(shè)計(jì)
