創設數學課堂情境提高學生思維品質

王春華

摘 ? 要：《數學課程標準》提出“學生的數學學習內容應當是現實的、有意義的、富有挑戰性的，這些內容要有利于學生主動地進行觀察、實驗、猜想、驗證、推理與交流”.這就要求教師在教學中要創設現實并且有吸引力的教學情境，使學生更容易地理解掌握數學知識和技能，促進學生對知識的主動建構，提高學生的思維品質.

關鍵詞：課堂情境;創設;提高;思維品質

對于情境創設在學生學習中的作用，德國一位學者有過一個精彩的比喻：將15克鹽放在你的面前，無論如何你難以下咽;但將15克鹽放入一碗美味可口的湯中，你早就在享用佳肴時，將15克鹽全部吸收了.情境之于知識，猶如湯之于鹽.鹽需溶入湯中，才能被吸收;知識需要溶入情境之中，才能顯示出活力和美感.《數學課程標準》把“注重提高學生的數學思維能力” [1]作為新課程的基本理念之一，數學思維能力是可以在教學活動中形成和發展起來的.在教學中，教師要善于創設合理的課堂情境，以培養學生的思維能力，提高學生的思維品質.下面就初中數學教學中的五個課堂情境案例的創設，談一些自己的看法和做法.

1 ? 借助生活經驗，創設生活情境

數學來源于生活，最終又服務于生活.選取具有生活氣息的現實情境，營造數學探究的氛圍，可以激發學生的好奇心和興趣;可以調動學生學習的主動性;可以喚起學生的數學思維，從而達到訓練思維的目的;還可以使學生對數學產生一種親和力，縮短與數學的心理距離，改進教學效果.

案例1 ? 筆者在教“概率”這一概念時，課前準備好教具：一個紙箱子、6個白色的乒乓球、6個黃色的乒乓球、獎品（若干根圓珠筆）.和學生互動，演示生活中的摸獎情景，告訴學生，規則是：摸中黃色的乒乓球有獎勵.第一環節，紙箱子里放6個黃色的乒乓球，叫學生上來摸球，每個學生都得到了獎品，為什么？讓學生思考.學生容易發現，因為里面的6個球都是黃球;第二環節，紙箱子里放6個黃球和6個白球，這時的情況是，有些同學中獎，有些同學沒中獎，為什么？第三環節，紙箱子里放6個白球，這時的結果，沒有一個同學中獎，為什么？讓學生在思考中得出本節課的幾個概念：必然事件、可能事件和不可能事件，學生很輕松的就掌握了本節課的內容.

事實上，在上這些課的時候，課堂氣氛很活躍，學生積極參與，根本原因是這些問題來自生活.創設貼近學生生活的情境，可以讓他們在興趣盎然中獲得積極的情感體驗，感受學習的樂趣，促使學生積極思維.

2 ? 通過故事或史料知識，創設故事情境

在數學的發展史上，有大量引人入勝的數學故事和數學史實.專家認為“教學的藝術不在于傳授本領而在于激勵、喚醒和鼓舞” [2 ]，因此我們在數學教學中，若能恰當地穿插和引用這些材料，給學生營造一個故事情境，不僅可以吸引學生的注意力，而且可以激發學生的數學學習興趣.用數學史實作為素材創設故事情境，有助于學生學習數學知識，對學生也是一種文化熏陶，有助于培養學生的創新思維.

案例2 ? 筆者在教“無理數”時，在講授無理數的概念時，先介紹它的歷史發展.古希臘的畢達哥拉斯學派認為，世間任何數都可以用整數或分數表示，并將此作為他們的一條信條.有一天，這個學派中的一個成員希伯斯（Hippasus）突然發現邊長為1的正方形的對角線是個奇怪的數，于是努力研究，終于證明出它不能用整數或分數表示.但這打破了畢達哥拉斯學派的信條，于是畢達哥拉斯命令他不許外傳，但希伯斯卻將這一秘密透露了出去，畢達哥拉斯大怒，要將他處死，希伯斯連忙外逃，然而還是被抓住了，被扔入了大海，為科學的發展獻出了寶貴的生命.希伯斯發現的這類數，被稱為無理數，無理數的發現，導致了第一次數學危機，為數學的發展做出了重大貢獻.

教師娓娓道來的故事緊緊地抓住了學生的好奇心，將學生帶入良好的學習情境當中，質疑激趣，充分調動了學生學習無理數的有關知識的積極性.通過這樣的數學史事，能讓學生感受先輩們追求真理的不屈不饒的精神，不但使學生產生濃厚的興趣，而且更能激發學生的探索新知的欲望.

3 ? 通過實驗操作，創設實驗活動情境

《新課程標準》倡導自主探索、動手實踐、合作交流、閱讀自學等學習數學的方式 [1 ].通過組織學生進行與數學知識有關的實驗活動或游戲，構建數學實驗情境，使學生在操作中提高學習數學的興趣，掌握數學知識，感受數學的情趣.創設實驗情境，以動啟思，以動促思，使學生的思維迅速地由抑制到興奮，積極參與，主動投入，在動手操作中萌發創新欲望，這樣可以培養學生思維的深刻性.

案例3 ? 教“一次函數”的第一課時時，老師說我們先做一個彈簧掛物體的實驗：這是自然長度為4cm的彈簧秤，在下面掛上不同的物體（已準備好砝碼）， 你們觀察它的長度有什么變化，把測量好的數據填入表1中相應的格內.一位學生協助教師量彈簧的長度，并填入表格.

表1

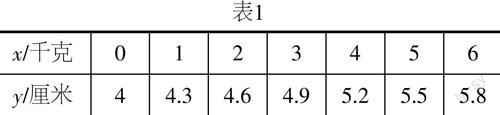
老師問同學們，從這些數據中你能發現什么規律？學生基本上異口同聲回答：當掛的物體重量每增加1千克時，彈簧就伸長0.3厘米.老師又問：彈簧長度（厘米）與物體重量（千克）的關系如何？學生還是能很輕松地回答：y=4+0.3x，老師評價：很好！我們還可以把它寫成y=0.3x+4.學生通過自己動手實驗，感受到做數學實驗的樂趣，并通過自己的實驗直觀地發現了函數關系式，這樣對抽象的函數關系式的理解、掌握會比較深刻.

“授人以魚，不如授人以漁”.學生通過對問題的思考，盡快地投入到新概念的探索中去，從而激發了學生的好奇以及探索創造的欲望.讓學生通過動手操作，使學生從實踐中獲得真知，讓學生體驗數學的樂趣，不僅調動了學生的積極性，而且啟發了學生的思維，有效地培養學生思維的獨創性.

4 ? 改變題目的條件或結論，創設變式問題情境

人類認識事物的過程是一個由易到難、由簡單到復雜、循序漸進的過程.在教學中，同一個題目，從不同的角度去分析研究，可以得到不同的啟迪，因而同樣一道題，可以擁有不同的解法.善于引導學生對不同解法的對比、變式，可以激發學生的學習興趣，可以提高學生思維的廣闊性、靈活性和深刻性.

案例4 ? 筆者在“平行四邊形的判定定理”教學中，選取了課本的習題：如圖1，在平行四邊形ABCD中，E、F分別在BC、AD上，且AF=CE.求證：四邊形AECF是平行四邊形.限時讓學生做，然后師生一起分析.

發現大部分學生用“一組對邊平行且相等的四邊形是平行四邊形”證明。

講完第一種方法后，老師發問：還有別的解法嗎？學生積極思考并發言，最后歸納出另外2種解法.解法2：用“定義——兩組對邊分別平行的四邊形是平行四邊形”;解法3：用“兩組對邊分別相等的四邊形是平行四邊形”.3種解法哪種最簡單？讓學生對比、發現、得出結論，解法1最簡潔，解法2、3比較繁瑣，通過證三角形全等得出.通過不同解法的對比，可以加深對知識的理解;可以培養學生思維的發散性、靈活性.一題多解講完后，再對此題進行變式.

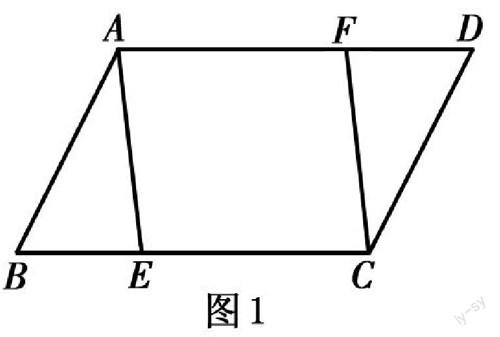
變式1：如圖1，“E、F分別在BC、AD上，且AF=CE”改為“E、F分別是BC、AD的中點”;

變式2：如圖1，“E、F分別在BC、AD上，且AF=CE”改為“E、F分別在BC、AD上，且DF=BE”;

變式3：如圖1，“AF=CE，求證：四邊形AECF是平行四邊形”改為“AE∥CF，求證：AE=CF”.

這組題中，變式1、變式2與習題相類似，讓學生體會：通過轉化仍能利用習題的解法解決此問題，從而加深學生對判定的理解，也培養學生由特殊到一般的歸納分析能力.變式3，也不難，但考察的知識點更多，要求對平行四邊形的判定與性質都掌握，才能快又準確地解決.如果能對一道題加以變式和延伸，不僅能使學生鞏固基礎知識，提高分析問題和解決問題的能力，而且對于溝通知識的聯系、開拓思路、培養思維都十分有益.

恰當合理的問題變式，有助于學生把知識學活;有助于學生舉一反三、觸類旁通;有助于學生產生學習的“最佳動機”和激發學生的靈感;有助于升華學生的思維，從而培養了學生思維的靈活性和發散性.為學生后續學習創造更好的條件、打下更堅實的基礎.

5 ? 通過錯題的分析，創設錯誤情境

在日常教學中，學生作業出現錯誤是不可避免的，課堂就是讓學生出錯的地方.實際上學生的錯題是我們教學的巨大財富.作為教師，我們不僅要寬容學生的錯題，更要將錯題視為發展學生智力的有效教學資源.面對學生的錯題，教師不能想當然，而是要善于與學生溝通，這樣才能幫助學生走出錯誤思維，提高學生思維的批判性.

案例5 ? 筆者在教“三角形三邊關系”時，提出一個問題：已知等腰三角形的一邊是4，另一邊是9，求周長.一學生如下作答：因為4+4+9=17或9+9+4=22，所以周長是17或22，同學們這答案對嗎？這是錯誤的！教師反問學生：周長會是17嗎？讓學生反思.學生不難發現：因為4+4<9，所以4、4、9不能構成三角形.所以答案為17是錯誤的.錯誤的根源在于沒有考慮“三角形的三邊關系”.筆者在教“勾股定理” 時，限時出了一道填空題，已知一個直角三角形的兩邊長分別為3cm和4cm，則第三邊為 ? ? ? .學生普遍的答案為5cm，我也輕松地說：由于同學們的粗心，很多同學都做錯了，想想錯在哪里？經過提醒，學生恍然大悟，要分類討論！還有一個答案■cm.又如：計算（x+1）2，學生A很快算出（x+1）2=x2+1，對嗎？我會搖搖頭說：錯！大錯特錯！因為結果漏了一項，忘了公式（a+b）2=a2+2ab+b2，很多同學想當然，都會犯（a+b）2=a2+b2這樣的錯誤.

通過創設錯誤情境，引導學生對錯題進行理性反思、辨別異同、探尋出錯的原因，讓學生在正確與錯誤的探索中發現錯誤的原因，不僅知其然，而且知其所以然，有效培養學生的良好思維，增強學生思維的嚴密性及批判性.

結束語

創設好的教學情境在數學教學中起著非常重要的作用.好的教學情境不僅可以激發學生學習數學的興趣，而且可以變“被動接受”為“主動探究”，還可以變“單一思維”為“多向拓展”，進而提高學生的思維品質，起到事半功倍的效果.“問渠哪得清如許，為有源頭活水來”.要想創設一個恰當而又優秀的數學教學情境，作為教師的我們務必要不斷的給自己充電，豐富自己的知識，拓寬視野，與時俱進，方有“活水”來.

參考文獻：

[1]中華人民共和國教育部.義務教育數學課程標準[S].北京：北京師范大學出版社，2012.

[2]呂傳漢，汪秉彝.論中小學“數學情境與提出問題”的教學[J].數學教育學報，2001（4）.