談如何創設情境提高高中數學課堂教學的有效性

邢昭良

【摘要】《普通高中數學課程標準》指出：“教材應注意創設情境，從具體實例出發，展現數學知識的發生、發展過程.使學生能夠從中發現問題、提出問題，經歷數學的發現和創造過程，了解知識的來龍去脈.”在有限的課堂教學里，要提高高中數學課堂教學的有效性，更應該下工夫研究問題情境創設.

【關鍵詞】高中數學；教學方法；課堂教學

眾所周知，數學是一門思維的科學.于是數學的教學自然而然就是一種思維的教學了.在課堂教學中，引導學生以知識為載體進行充分的思維活動就是老師的主要任務.而思維來自于什么呢？來自于問題.所以對于一節課來說，如何在開頭以一個巧妙的問題切入，使學生一下子就進入活躍的思維狀態是一節課成敗的關鍵.下面，以我在教學中的實踐經驗例談如何巧妙創設情境，提出有效問題激發學生的思維活動，提高課堂教學的有效性.

一、創設趣味問題情境，深刻理解相關概念

《普通高中數學課程標準》在“教學建議”中指出：“教學中應強調對基本概念和基本思想的理解和掌握，對一些核心概念和基本思想（如函數、空間觀念、運算、數形結合、向量、導數、統計、隨機觀念、算法等）要貫穿高中數學教學的始終，幫助學生逐步加深理解.由于數學高度抽象的特點，注重體現基本概念的來龍去脈.在教學中要引導學生經歷從具體抽象出數學概念的過程，在初步運用中逐步理解概念的本質.”因此新的基本概念的出現，應下大工夫創設趣味問題情境，讓學生饒有興趣地經歷從具體實例抽象出數學概念的過程.

案例一

在學習概率部分時，為了更好地理解獨立事件與互斥事件這一概念，我使用了以下情境問題引入：

一位王子向智慧公主求婚，智慧公主為了考驗王子的智慧，就讓仆人端來兩個盤，其中一個裝著10枚金幣，另一個裝著10枚同樣大小的銀幣.仆人把王子的眼睛蒙上，并把兩個盤的位置隨意調換，請王子隨意選一個盤，從里面挑選出一枚硬幣.如果選中的是金幣，公主就嫁給他；如果選中的銀幣，那么王子就再也沒有機會了.王子聽了說：“能不能在蒙上眼睛之前，任意調換盤里的硬幣組合呢？”公主同意了.請問：王子該怎樣調換硬幣才能確保更有把握娶到公主呢？

經過計算發現，把銀幣放入金幣的盤里或兩個盤互換幾個時，摸到金幣的概率都會小于0.5；而把金幣放入銀幣的盤里時，摸到金幣的概率會大于0.5.于是產生了一個新的問題：放幾個時，摸到金幣的可能性最大？經過計算發現，放1個的概率<放2個的概率<放3個的概率<……但如果把金幣全部放入概率又回到了0.5.于是得到最終的調換方案如下：

王子在裝有金幣的盤里留1枚金幣，把另外9枚金幣倒入放銀幣的盤里，這樣原來放銀幣的盤里就有10枚銀幣和9枚金幣.如果他選中那個放1枚金幣的盤，選中金幣的概率為100%；如果選中放19枚錢幣的盤，摸到金幣的概率為9[]19.王子選中每個盤的概率均為1[]2，所以王子選中金幣的概率就是100%×1[]2+9[]19×1[]2=14[]19.如果不做任何調換，王子摸到金幣的概率只有1[]2，顯然，調換后王子摸到金幣的概率大大增加.計算中互斥事件和獨立事件不可避免地出現了，于是互斥事件有一個發生的概率以及獨立事件同時發生的概率在不知不覺中在應用中學習了.

二、創設關聯問題情境，引導學生創新發現

《普通高中數學課程標準》在“教學建議”中還指出：“高中數學課程是以模塊和專題的形式呈現的.因此，教學中應注意溝通各部分內容之間的聯系，通過類比、聯想、知識的遷移和應用等方式，使學生體會知識之間的有機聯系，感受數學的整體性，進一步理解數學的本質，提高解決問題的能力.”

案例二

在學習“導數”這一概念時，我創設了這樣的問題情境：

1.如何求過圓x2+y2=10上一點P（1，3）的圓的切線方程？（注：可以利用圓的切線性質或圓心到切線的距離等于半徑求得）

2.如何求過拋物線y=x2上的點P（1，1）的拋物線的切線方程？（注：可以利用直線與橢圓聯立，判別式為0求得）

3.如何求過曲線y=x3上的點P（1，1）的曲線的切線方程？

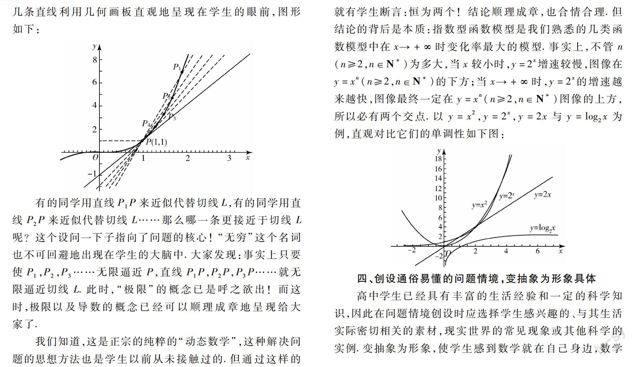
利用幾何畫板，要解決的問題直觀地呈現給學生：

我們要求的就是圖中P點處切線L的方程，現在的難點在于無法精確求得，于是提出問題：近似求得L的方程呢？學生都認為這沒問題！而且一下子求出了很多，選擇幾條直線利用幾何畫板直觀地呈現在學生的眼前，圖形如下：

有的同學用直線P1P來近似代替切線L，有的同學用直線P2P來近似代替切線L……那么哪一條更接近于切線L呢？這個設問一下子指向了問題的核心！ “無窮”這個名詞也不可回避地出現在學生的大腦中.大家發現：事實上只要使P1，P2，P3……無限逼近P，直線P1P，P2P，P3P……就無限逼近切線L.此時，“極限”的概念已是呼之欲出！而這時，極限以及導數的概念已經可以順理成章地呈現給大家了.

我們知道，這是正宗的純粹的“動態數學”，這種解決問題的思想方法也是學生以前從未接觸過的.但通過這樣的情境設置，學生能夠以一種最自然的方式認識它、接受它，進而深深植根融合于他們已有的知識體系之中，也為后面順利探究定積分以及微積分基本定理提供了一次示范.

三、創設感興趣的問題情境，激發學生探究熱情

在數學教學中，應注重發展學生的應用意識；通過豐富的實例引入數學知識，引導學生應用數學知識解決實際問題，經歷探索、解決問題的過程，體會數學的應用價值.幫助學生認識到：數學與我有關，與實際生活有關，數學是有用的，我要用數學，我能用數學.從而激發學生的數學探究熱情.

案例三

在學習指數函數時，為了給學生指數函數的單調性變化速度的一個精準認識（與冪函數與對數函數的比較），我先在教學中選擇了一個這樣的生活化情境問題（來自百度）：

一張足夠大的普通薄紙，把它一直對折，折30次后有多高？

答案是不可思議的！計算如下：

一張普通的薄紙大約厚度為0.08 mm，

0.08×230÷1000=85899.34592（m），大約相當于10個珠穆朗瑪峰高！

為真正認識清楚指數函數與冪函數遞增區別，設置以下問題：函數y=2x與函數y=xn（n≥2，n∈N*）在第一象限有幾個交點？

學生的直覺都是錯誤的.于是化繁為簡：就最簡單的y=2x與y=x2（即n=2時）的圖像在第一象限的交點有幾個呢？通過計算和幾何畫板展示有兩個交點.之后趁熱打鐵：n=3呢？n=4呢？經過一番探究，有幾個悟性較高的學生發現交點是兩個.檢驗是簡單的，幾何畫板直觀明了毫無爭議.之后拓展升華：對一般的n（n≥2，n∈N*）呢？馬上就有學生斷言：恒為兩個！結論順理成章，也合情合理.但結論的背后是本質：指數型函數模型是我們熟悉的幾類函數模型中在x→+∞時變化率最大的模型.事實上，不管n（n≥2，n∈N*）為多大，當x較小時，y=2x增速較慢，圖像在y=xn（n≥2，n∈N*）的下方；當x→+∞時，y=2x的增速越來越快，圖像最終一定在y=xn（n≥2，n∈N*）圖像的上方，所以必有兩個交點.以y=x2，y=2x，y=2x與y=log2x為例，直觀對比它們的單調性如下圖：

四、創設通俗易懂的問題情境，變抽象為形象具體

高中學生已經具有豐富的生活經驗和一定的科學知識，因此在問題情境創設時應選擇學生感興趣的、與其生活實際密切相關的素材，現實世界的常見現象或其他科學的實例.變抽象為形象，使學生感到數學就在自己身邊，數學應用無處不在.

案例四

我在講解“二分法”時，設置了這樣的問題情境：授課前，我準備了一臺價值67元的計算器.創設問題為：已知這臺計算器的價格在200元之內，如果誰能在10秒之內猜出這臺計算器的價格，我就把這臺計算器送給這名同學.

經過大家幾番共同的修正與改進，發現最快的猜測如下：先猜100（這是0與200的中間數，此時我會說高了），然后猜50（這是0與100的中間數，此時我會說“低了”），然后再猜75（這是50與100的中間數，此時我會說“高了”），然后猜60（低了），然后猜70（高了），然后猜65（低了），然后即馬上猜中.

這里用到的方法就是數學中典型的“二分法”.通過這樣一個具體的情境淺顯地呈現于大家的面前后，再講解課本中應用于數學里“二分法”就使學生很容易接受.它使抽象的方法變得形象具體，使學生覺得馬上就可以動手操作.

創設有效的問題情境，不僅能夠激發學生的學習興趣，而且能夠培養學生自主地探索、解決問題的能力.教師在數學教學過程中要了解學生不喜歡數學的原因，并要善于挖掘教材潛力，下大工夫創設美好的數學情境教學，以便激勵、喚醒、鼓舞學生，激發學生飽滿的學習熱情，促使他們以積極的態度和旺盛的精力主動求索，從而獲得課堂教學的最佳效果.

【參考文獻】

[1]普通高中數學課程標準研制組.普通高中數學課程標準.人民教育出版社，2003：108-117.

[2]張燕順.數學的思想、方法和應用（修訂版）.北京：北京大學出版社，2005：249-272.