小學(xué)計(jì)算教學(xué)中聯(lián)想能力的培養(yǎng)

林成蔭

【關(guān)鍵詞】計(jì)算教學(xué) 聯(lián)想能力 思維發(fā)展

【中圖分類號】G 【文獻(xiàn)標(biāo)識碼】A

【文章編號】0450-9889（2015）06A-0077-01

小學(xué)數(shù)學(xué)計(jì)算教學(xué)的編排由淺入深，由簡單到復(fù)雜，螺旋上升，相互關(guān)聯(lián)，形成系統(tǒng)，為培養(yǎng)學(xué)生的聯(lián)想能力提供了重要的知識載體。教師應(yīng)根據(jù)同類數(shù)的同種運(yùn)算、不同數(shù)間的同種運(yùn)算及運(yùn)算定律的應(yīng)用和驗(yàn)算等知識的不同特點(diǎn)來培養(yǎng)學(xué)生的聯(lián)想能力，使學(xué)習(xí)效果、聯(lián)想能力和思維品質(zhì)三者共同發(fā)展。

一、啟發(fā)縱向聯(lián)想，培養(yǎng)深刻思維

縱向聯(lián)想是根據(jù)教材的系統(tǒng)性，由淺入深，由易到難的聯(lián)想。小學(xué)教材主要學(xué)習(xí)加減乘除四種運(yùn)算，根據(jù)學(xué)生的認(rèn)知規(guī)律和知識的內(nèi)在聯(lián)系，每一種運(yùn)算教材都是由簡單到復(fù)雜來進(jìn)行編排，比如，加減法的運(yùn)算是從“20以內(nèi)”到“100以內(nèi)”再到“萬以內(nèi)”的順序編排，乘法是從“表內(nèi)乘法”到“多位數(shù)乘一位數(shù)”，再到“兩位數(shù)乘兩位數(shù)”，最后是“三位數(shù)乘兩位數(shù)”來編排的……教師可以根據(jù)教材的編排特點(diǎn)和知識的內(nèi)在聯(lián)系，啟發(fā)學(xué)生在學(xué)習(xí)除“20以內(nèi)加減法、表內(nèi)乘法和表內(nèi)除法”這些起點(diǎn)性的運(yùn)算外的其他運(yùn)算時(shí)，可進(jìn)行縱向聯(lián)想，想一想與該運(yùn)算相關(guān)的已學(xué)的算理和算法，再將已學(xué)的算理和算法遷移到新的運(yùn)算中，再授予學(xué)生自主探索新知的方法，使學(xué)生的思維由淺入深，由現(xiàn)象到本質(zhì)，培養(yǎng)學(xué)生思維的深刻性。例如，在教學(xué)列豎式計(jì)算376+284時(shí)，先引導(dǎo)學(xué)生聯(lián)想兩位數(shù)加兩位數(shù)是怎么算的？學(xué)生會想到相同數(shù)位對齊，從個(gè)位加起，滿十進(jìn)一的計(jì)算方法，接著讓學(xué)生嘗試運(yùn)用這種方法計(jì)算這道題，在此過程中，實(shí)現(xiàn)知識的遷移，促使學(xué)生的知識系統(tǒng)化、方法靈活化、思維廣闊化和深度化。

從整數(shù)四則運(yùn)算到小數(shù)四則運(yùn)算再到分?jǐn)?shù)四則運(yùn)算的編排，同樣可引導(dǎo)學(xué)生進(jìn)行縱向理想。例如，學(xué)生第一次學(xué)習(xí)計(jì)算小數(shù)加法時(shí)，可以先讓學(xué)生回憶整數(shù)加法是怎么計(jì)算的？接著提出引導(dǎo)性問題：小數(shù)加法是不是也應(yīng)該相同數(shù)位對齊，也就是相同的計(jì)數(shù)單位相加？通過與具體情境的聯(lián)系和思考，學(xué)生很快明白小數(shù)加法也應(yīng)該是相同的計(jì)數(shù)單位相加，而相同計(jì)數(shù)單位相加，在小數(shù)加法中即小數(shù)點(diǎn)對齊相加。由此，可以聯(lián)想到計(jì)算小數(shù)減法也應(yīng)該是同樣的道理。到五年級學(xué)分?jǐn)?shù)加減法時(shí)，也用同樣的方式啟發(fā)聯(lián)想，從而讓學(xué)生明白分?jǐn)?shù)加減法也是要相同的計(jì)數(shù)單位即分母相同才能相加減，這樣就溝通了知識之間的聯(lián)系，使新舊知識聯(lián)系起來，構(gòu)建知識體系。

二、引導(dǎo)橫向聯(lián)想，培養(yǎng)發(fā)散思維

橫向聯(lián)想是不同事物間的相關(guān)性的聯(lián)想。小學(xué)數(shù)學(xué)四則運(yùn)算的教學(xué)目的，不僅是學(xué)生會根據(jù)法則正確計(jì)算，理解運(yùn)算的算理，還能夠根據(jù)題目條件尋求簡捷、合理的運(yùn)算途徑。學(xué)習(xí)五大運(yùn)算定律后，學(xué)生在遇到計(jì)算題時(shí)，就能根據(jù)題目的條件進(jìn)行多角度、多方向的聯(lián)想，從而產(chǎn)生多種解法。例如，計(jì)算2.5×44，學(xué)生想到的最基本的方法是列豎式計(jì)算。教師還要引導(dǎo)學(xué)生觀察數(shù)據(jù)特點(diǎn)，聯(lián)系乘法分配律，又想到2.5×（40+4）的計(jì)算方法。2.5×4或40能湊成整十?dāng)?shù)，但多位數(shù)乘一位數(shù)口算也很方便，于是根據(jù)乘法分配律，還可把2.5看成2+0.5，即用（2+0.5）×44來計(jì)算。此外，因數(shù)中的數(shù)可看成兩數(shù)相加，那么也可以看成兩數(shù)相減，所以（3-0.5）×44和2.5×（50-6）也很容易算；又想到44也可看成4×11，那么根據(jù)乘法結(jié)合律，也可變換成2.5×4×11來計(jì)算。這種橫向聯(lián)想，溝通了知識之間的聯(lián)系，產(chǎn)生了多樣化的解題方法，使學(xué)生的思維更加寬廣，發(fā)展了他們的求異思維和發(fā)散思維，提高了他們的思維品質(zhì)。

三、指引可逆聯(lián)想，培養(yǎng)靈活思維

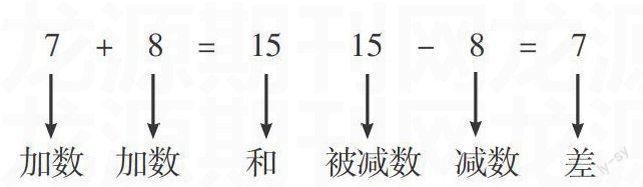
可逆聯(lián)想是條件和結(jié)論間的雙向聯(lián)想。加減法是互逆的運(yùn)算，乘除法也是互逆的運(yùn)算，利用它們的互逆，可以指引學(xué)生可逆聯(lián)想，避免造成思維的刻板。例如，學(xué)生由一道加法算式寫出兩道減法算式中觀察到“加數(shù)+加數(shù)=和”，那么“和-一個(gè)加數(shù)=另一個(gè)加數(shù)”，從而得出驗(yàn)算加法的方法。而減法的驗(yàn)算要從加法入手，逆向思考，減數(shù)和差是加法算式中的兩個(gè)加數(shù)，被減數(shù)是和（如圖所示），所以驗(yàn)算減法就由被減數(shù)（即和）減差（即一個(gè)加數(shù)）看是否得減數(shù)（即另一個(gè)加數(shù)），或減數(shù)（即一個(gè)加數(shù)）加差（即另一個(gè)加數(shù)）是否得被減數(shù)（即和）這兩種方法。

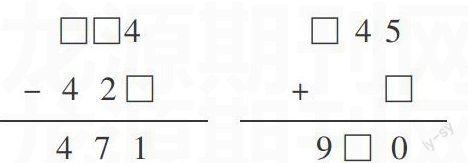
當(dāng)學(xué)生掌握了加減法驗(yàn)算的基本方法后，教師可以設(shè)計(jì)練習(xí)，訓(xùn)練學(xué)生進(jìn)行雙向聯(lián)想，培養(yǎng)學(xué)生思維的靈活性。

總之，小學(xué)數(shù)學(xué)計(jì)算中的四則運(yùn)算和驗(yàn)算及運(yùn)算定律這三大方面，各有特點(diǎn)，教師可根據(jù)它們的特點(diǎn)采用不同類型的聯(lián)想思維進(jìn)行引導(dǎo)，既使學(xué)生能扎實(shí)靈活地掌握知識，又能培養(yǎng)學(xué)生的聯(lián)想能力，同時(shí)還可以提高學(xué)生的思維品質(zhì)。

（責(zé)編 林 劍）