引導(dǎo)學(xué)生開啟探究學(xué)習(xí)之旅

張文麗

摘要：義務(wù)教育階段數(shù)學(xué)課程的最終目標(biāo)是為學(xué)生的終身學(xué)習(xí)和發(fā)展奠定基礎(chǔ)，這就需要教師把握教材的編寫意圖，根據(jù)學(xué)生的年齡特點(diǎn)和認(rèn)知規(guī)律，適時(shí)地組織探究學(xué)習(xí)活動，為學(xué)生提供探究學(xué)習(xí)的舞臺，讓每個(gè)學(xué)生成為學(xué)習(xí)活動的參與者、實(shí)踐者、研究者、探索者。

關(guān)鍵詞：引導(dǎo)；開啟；探究學(xué)習(xí)

中圖分類號：G623.5文獻(xiàn)標(biāo)識碼：A 文章編號：1992-7711（2015）15-089-2

“教是為了不教”，作為蘇派課堂教學(xué)改革的特色，很多學(xué)校都在實(shí)踐和研究。筆者認(rèn)為，教師首先要從自己的課堂入手，把握好教材，根據(jù)學(xué)生的年齡特點(diǎn)和認(rèn)知規(guī)律，適時(shí)地組織探究學(xué)習(xí)活動，逐步形成良好的自主探究的意識和習(xí)慣，積累探究學(xué)習(xí)的活動經(jīng)驗(yàn)，為以后的學(xué)習(xí)之旅積聚力量。那么，數(shù)學(xué)探究學(xué)習(xí)該如何做到“形”、“神”皆備呢？下面談?wù)劰P者在實(shí)踐中的做法：

一、立足課堂，讓每個(gè)學(xué)生都成為研究者

深入挖掘教材是引導(dǎo)學(xué)生進(jìn)行探究學(xué)習(xí)的基礎(chǔ)。雖說，學(xué)生接受的都是前人的經(jīng)驗(yàn)，但如果是由自己思考研究發(fā)現(xiàn)的，那么在孩子們牢固掌握知識之余，還能積累探究學(xué)習(xí)的經(jīng)驗(yàn)，點(diǎn)亮創(chuàng)新思維的火花。

例：蘇教版小學(xué)數(shù)學(xué)四年級下冊第33頁“積的變化規(guī)律”。

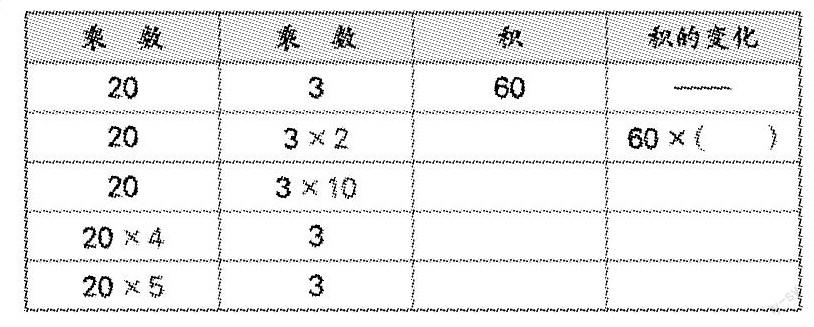
課前作為前置性作業(yè)，讓學(xué)生先填表，再說說有什么發(fā)現(xiàn)？

課堂上的“重頭戲”則放在讓學(xué)生說說自己的發(fā)現(xiàn)，讓孩子們自己去糾正、補(bǔ)充、完善，然后組織全班交流：

生1：我發(fā)現(xiàn)一個(gè)乘數(shù)不變，另一個(gè)乘數(shù)變化，積也會發(fā)生變化。

生2：一個(gè)乘數(shù)不變，另一個(gè)乘數(shù)乘上幾，積也乘幾。

師：你能照樣子接著寫幾個(gè)嗎？

生：寫不完。

師：現(xiàn)在你能再說說你的發(fā)現(xiàn)嗎？

生：一個(gè)乘數(shù)不變，另一個(gè)乘數(shù)乘幾，積就等于原來的積乘積。

師：同學(xué)們的發(fā)現(xiàn)能不能成為一個(gè)計(jì)算規(guī)律呢？請同學(xué)們再找一些例子算一算、比一比，看看積的變化是不是有同樣的規(guī)律。

生：12×5=60（12×2）×5=60×2=12012×（5×10）=60×10=600……

師：現(xiàn)在你想說什么？

生：“一個(gè)乘數(shù)不變，另一個(gè)乘數(shù)乘幾，積就等于原來的積乘積。”

師：誰能給發(fā)現(xiàn)的規(guī)律取名？

生：上學(xué)期，我們學(xué)過商不變規(guī)律，這個(gè)就叫積的變化規(guī)律吧！

師：你和數(shù)學(xué)家想到一塊去了，這個(gè)規(guī)律就叫積的變化規(guī)律。

那么積只有在一個(gè)乘數(shù)不變，另一個(gè)乘數(shù)乘幾時(shí)，才會發(fā)生變化嗎？

生：我覺得一個(gè)乘數(shù)不變，另一個(gè)乘數(shù)除以幾時(shí)，積也是變化的。

師：怎樣變化的呢？我們動手驗(yàn)證一下。（生再次嘗試）

生：20×30=600（20÷2）×30=600÷2=300

20×（30÷10）=600÷10=60……

師：誰能完整說說什么是積的變化規(guī)律？（生試著說）

生：我們在學(xué)除法時(shí)，已經(jīng)知道除數(shù)不能為0，所以這里也要0除外。

這樣“積的變化規(guī)律”自然“出生”，比教材的內(nèi)容更豐滿。學(xué)生從感性認(rèn)識到理性認(rèn)識，其實(shí)是一個(gè)暴露思維的過程，自己去試一試，讓學(xué)生經(jīng)歷一番“磨難”取到“真經(jīng)”，遠(yuǎn)比老師一味地灌輸、反復(fù)地練習(xí)要深刻地多。正所謂“看了會忘記，寫了會知道，做了會記住”。

二、體驗(yàn)生活，讓每個(gè)學(xué)生都成為實(shí)踐者

數(shù)學(xué)課程標(biāo)準(zhǔn)中對體驗(yàn)學(xué)習(xí)提出了明確的要求，每冊均安排了實(shí)踐活動，為學(xué)生創(chuàng)新意識和實(shí)踐能力的培養(yǎng)提供了很好的機(jī)會。

例：在蘇教版小學(xué)數(shù)學(xué)四年級下冊第46頁“一億有多大”。

師：通過前面的學(xué)習(xí)，誰能說說一億有多大？

生：1億是10個(gè)一千萬；100個(gè)一百萬是1億；1000個(gè)十萬是1億。

生：前面我們推算過，1億張紙的厚度大約是10000米，1億個(gè)1元硬幣大約重600噸。

師：那你們知道數(shù)1億本練習(xí)本大約要用多長時(shí)間嗎？

生：1個(gè)多小時(shí)；2天；一個(gè)月；要一年多吧！

師：怎樣證明誰猜的準(zhǔn)一些呢？你們有什么好辦法？

生：1億本太多，可以先數(shù)10本或100本，再進(jìn)行推算。

生：10本太少了，我覺得100本比較合適。

4人小組合作，一人數(shù)100本練習(xí)本，一人計(jì)時(shí)，兩人做記錄；然后以數(shù)100本練習(xí)本的時(shí)間為參照，逐步推算出，照這樣的速度，數(shù)1億本所需用的時(shí)間。小組匯報(bào)：

生：數(shù)1億本大約要用9千萬秒。

師：數(shù)一億本練習(xí)本大約是多少小時(shí)？多少天？多少年呢？請大家用計(jì)算器算一算。

（學(xué)生在計(jì)算之余，不禁發(fā)出“哇塞”的驚叫聲）

生：大約要2年多，三年不到一點(diǎn)。

師：這是按每天數(shù)24小時(shí)計(jì)算的，如果按每天工作8小時(shí)計(jì)算，大約要數(shù)幾年？

生：要八年多。

師：看這個(gè)計(jì)算結(jié)果，你有什么想說的？

生：1億本太多了，數(shù)的時(shí)間太長了……

在“數(shù)一數(shù)”活動之后，又組織了“量一量”、“稱一稱”這兩個(gè)體驗(yàn)活動。課堂上學(xué)生借助比較熟悉的事物數(shù)量來推算1億有多大，每次體驗(yàn)活動都會讓學(xué)生發(fā)出驚叫聲。可見，從量的角度，學(xué)生感受到了1億這個(gè)數(shù)的實(shí)際大小，把抽象的數(shù)轉(zhuǎn)化成了可感知的量，增強(qiáng)了學(xué)生對大數(shù)的把握能力。

三、倡導(dǎo)合作，讓每個(gè)學(xué)生都成為參與者

教師該扮演怎樣的角色？怎樣營造寬松、和諧、民主的學(xué)習(xí)氛圍，適時(shí)地介入學(xué)生的活動，不干涉學(xué)生的思考和探索，并充分地為他們提供合作討論、發(fā)表意見的時(shí)間和機(jī)會呢？

例：蘇教版小學(xué)數(shù)學(xué)四年級下冊第39頁第7題，聯(lián)系具體的實(shí)例，學(xué)生在對乘法算式中兩個(gè)乘數(shù)同時(shí)變化而引起的積變化的規(guī)律，將前面已學(xué)的積的變化規(guī)律進(jìn)行了拓展和延伸。就在此時(shí)，有一學(xué)生弱弱地嘀咕道：既然有“積的變化規(guī)律”，那么一定也有“積不變規(guī)律”。旁邊學(xué)生反擊道“書上又沒有講，你能舉個(gè)例子來說明嗎？”學(xué)生的思維是很活躍的，有時(shí)冒冒失失提出的問題，卻是一個(gè)很好的研究素材，不如順?biāo)浦郏黄饋碛懻摪桑?/p>

果然，學(xué)生列舉了很多個(gè)積不變的例子，通過對比還發(fā)現(xiàn)了有趣的規(guī)律：一個(gè)乘數(shù)乘幾，另一個(gè)乘數(shù)除以相同的數(shù)（0除外），積不變。

教師要善于捕捉學(xué)生的思想動態(tài)，要有“放”的胸懷，為學(xué)生搭建展開思維翅膀的舞臺，讓學(xué)生扇動思想的羽翼飛得更高更遠(yuǎn)。

四、突破傳統(tǒng)，讓每個(gè)學(xué)生都成為探索者

隨著信息技術(shù)的迅猛發(fā)展，互聯(lián)網(wǎng)更具超大信息量。在認(rèn)識了近似數(shù)后，讓學(xué)生課后上網(wǎng)收集一些近似數(shù)，體會它在生活中的價(jià)值；在認(rèn)識了多位數(shù)后，讓學(xué)生上網(wǎng)調(diào)查世界七大洲的人口分布情況，體會大數(shù)目在生活中的應(yīng)用；在學(xué)生掌握了十進(jìn)制計(jì)數(shù)法后，帶領(lǐng)學(xué)生去電腦房，自己去上網(wǎng)查找，了解除十進(jìn)制計(jì)數(shù)法之外，還有什么計(jì)數(shù)法？如何將十進(jìn)制和二進(jìn)制進(jìn)行互相轉(zhuǎn)化？拓寬學(xué)生的數(shù)學(xué)視野，將課內(nèi)學(xué)習(xí)延伸至課外，將書本知識拓展到人文科學(xué)領(lǐng)域，讓每個(gè)學(xué)生都能成為探索者，讓學(xué)生置身于更廣闊的學(xué)習(xí)空間中。

作為教師，只有真正了解學(xué)生思維活動過程，才能科學(xué)合理地進(jìn)行設(shè)計(jì)，巧妙機(jī)智地予以點(diǎn)撥，在提高探究學(xué)習(xí)效益的同時(shí)，培養(yǎng)和發(fā)展學(xué)生的創(chuàng)新意識和實(shí)踐能力。