善用幾何教學的利器——分析法與綜合法
王海祥
摘要:數學對于人的發展作用歷來以“促進人的邏輯思維、理性精神”為顯著標志,而這一極為重要的作用往往需要通過發展學生“數學推理能力”的教學來實現。幾何教學對學生推理能力的發展作用是不言而喻的。本文以《圓中的相似問題》教學為例,就幾何教學中如何發展學生的推理能力進行了探討。
關鍵詞:幾何教學;推理能力;分析與綜合
中圖分類號:G633.6 文獻標識碼:A 文章編號:1006-3315(2015)07-031-002
推理能力是《義務教育數學課程標準》提出的十大數學課程核心概念之一。發展學生的推理能力歷來是數學課程的一個重要功能,幾何教學對學生推理能力的發展作用是不言而喻的。如何在幾何教學中發展學生的推理能力,是幾何教學的重中之重。
本人有幸在蘇州市初中課改展示活動中開設了一節教學公開課——《圓中的相似問題》,備課過程中一直在思考這樣一個問題:“這一節課,要留給學生的到底是什么?要給那些不辭辛苦、遠道而來的老師們帶回去些什么?”經過反復思量后,決定將幾何學習最本質、最重要的東西留給這些學生——推理能力,同時也要將幾何教學中最本質、最重要的東西傳遞給這些老師——幾何教學關鍵在于培養孩子的推理能力。在備課、上課、反思這樣一系列的環節結束后,本人有了一些粗淺的想法,整理出來,以饗同仁,用作交流。
一、從“未知”出發,發展學生逆向分析思考能力
“分析法”是演繹推理的一個重要的方法,一個學生分析問題能力的高低,往往決定著這個學生解決問題能力的強弱。本人結合自身平時的教學及此次公開課的實踐經驗發現,采用“箭頭式”的反推分析,對提高學生的推理能力非常有利,條理也非常清晰。
案例一:如圖,在⊙O中,弦AB、CD相交于圓內一點E.求證:AE·BE= CE·DE.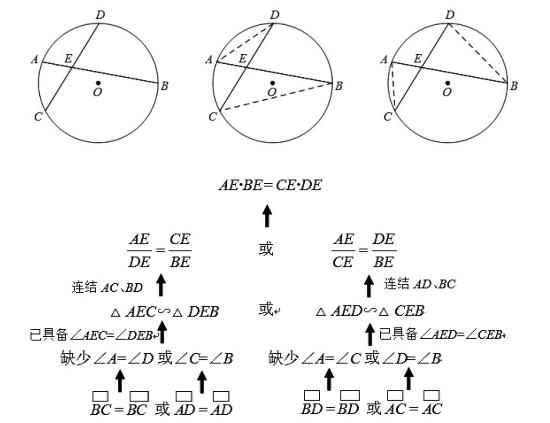
在培養學生逆向分析思考能力時,具體的表現形式實際上是次要的,關鍵在于要通過教師有意識的引導,培養學生分析問題的“分析意識”。有了“意識”,學生才會在遇有問題時,去嘗試“分析”,久而久之,形成一種思考的習慣,最終形成思維能力。
二、從“已知”出發,發展學生順向綜合思考能力
任何問題的解決都是建立在“已知條件”的基礎上的,僅僅通過逆向分析思考,有時會使得問題一下子變得復雜,這時候,我們就要學會從這些“已知條件”上去挖掘“信息”。常規的數學問題,往往是以完整的問題形式給出,即:題目的條件和結論一起給出。這樣的呈現方式有一個弊端,就是不利于學生推理方法的形成。筆者在實際教學中發現,“結論開放性”問題的設置可以很好地解決這一問題,即:設置“只給題干和圖形,自行推導、發現結論”類的問題。
案例二:
(1)如圖,△ABC內接于⊙O,AE平分∠BAC,交BC于D,交⊙O于E,連結BE.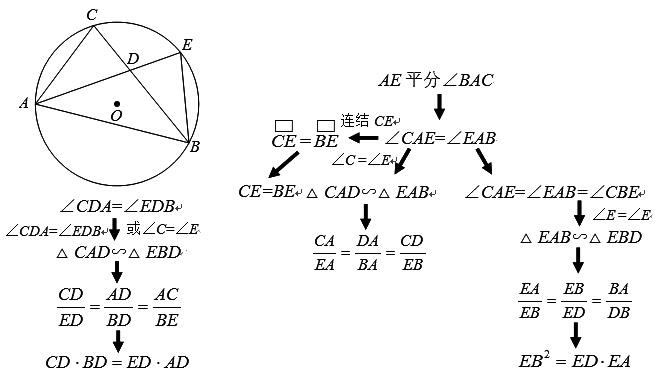
(2)在上題中,若添加條件:“AB為⊙O的直徑,BE=4,DE=2”,你能求出哪些線段的長度?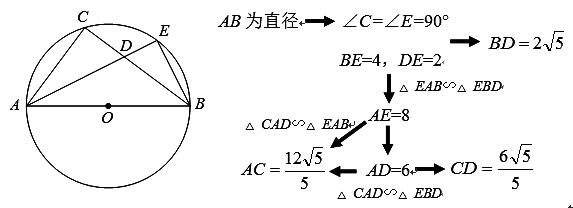
“結論開放性”問題,也可以適時地讓學生根據題干自主命題,即:學生出題,學生解題。以激發學生的學習興趣、學習熱情,同時也可以培養學生的逆向和順向推理能力。
三、從“兩頭”出發,發展學生邏輯推理能力
數學問題的奇妙在于這些看似簡單的數字和圖形中,蘊藏著無窮的奧妙。一個比較完整的數學問題,尤其是幾何問題,它的思考過程往往需要一個“雙向”的思維過程,即:從“已知”和“未知”兩個方向去思考問題。
案例三:如圖,已知點E在Rt△ABC的斜邊AB上,以AE為直徑的⊙O與直角邊AC相交于點F,與直角邊BC相切于點D.若AB=10,AC=6,試求線段AF的長.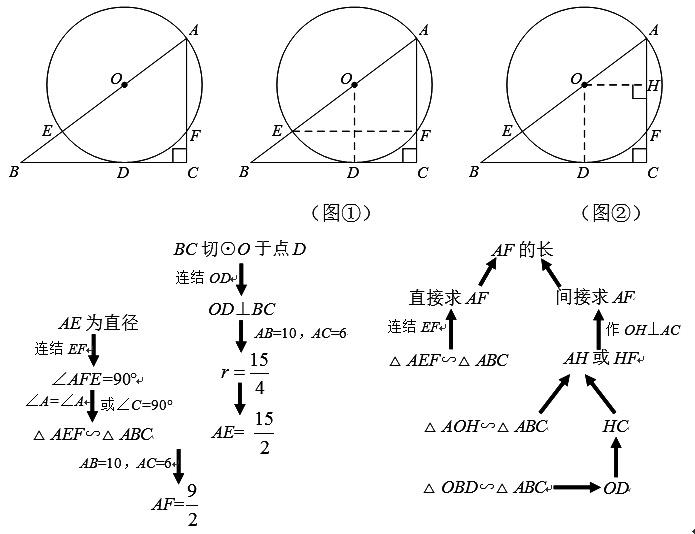
通過“雙向”分析上述問題至少存在兩種解決方案。當然,在實際解決問題時,不一定每個問題都要求學生分析的面面俱到,“面面俱到”有時反而會使問題顯得復雜。但是引導學生自己感悟,解決問題實際上是在“已知”和“未知”之間搭建“橋梁”,尋找“關聯點”,這一點很重要。
四、結束語
數學對于人的發展作用歷來以“促進人的邏輯思維、理性精神”為顯著標志,而這一極為重要的作用往往需要通過發展學生“數學推理能力”的教學來實現。數學推理包含合情推理和演繹推理,它們在解決問題的過程中雖功能有所不同(合情推理主要用于探索思路、發現結論,演繹推理用于證明結論),但卻是相輔相成的,教學時要注重合情推理和演繹推理的有機融合。當學生的推理能力真真切切地達到一定的境界,這種能力就會體現在學習、生活的各個方面,學生會逐步形成一種審視、處理問題的方式,教育的價值也就能充分實現。
參考文獻:
[1]《義務教育數學課程標準(2011年版)》,北京師范大學出版集團, 2012.1
[2] 姜秀勤, 宣玉清. 注重初中幾何邏輯推理能力的教學, 吉林教育,2003(3)
[3] 周茂生. 幾何教學中學生邏輯推理能力的培養,中學數學雜志(初中),2005(8)
[4] 呂秀娟. 在幾何教學中如何培養學生的推理能力,上海教育 ,998(8)

