基于課本資源的“微專題”教學實踐與思考

【摘 要】在高三后期有效地穿插“微專題”，可以彌補傳統的高三復習教學中的一些不足與缺陷。“阿波羅尼斯圓”教學設計為例，反思微專題教學的幾個關鍵環節：課題的確定，遵循真、小、實的原則;課型的教學設計，注重知識的整合，突出以小見大;習題的選擇突出見微知著以及“微專題”教學注重教學的生成性，以便提高高三復習教學的有效性。

【關鍵詞】微專題;課本資源;教學實踐

【中圖分類號】G633.6 【文獻標志碼】A 【文章編號】1005-6009（2015）42-0032-03

【作者簡介】李寬珍，江蘇省溧水高級中學（南京，211200）教師，中學高級教師。

專題復習是高三數學復習后期的重要階段。它是在一輪復習的整體梳理、知識網絡建構之后，必須經歷的以綜合訓練為主，以訓練解題能力和優化思維品質為最終目的的復習階段。如何提高這一階段的復習效率呢？筆者經過幾屆畢業班的教學，發現在高三后期的專題復習中，“微專題”復習是對數學專題復習的有效補充，對學生掌握難點問題、查漏補缺有很好的幫助。近幾年的高考中，以“阿波羅尼斯圓”為背景的試題一度成為考查熱點，而此背景源自課本，由此，筆者基于課本資源開設了一節關于“阿波羅尼斯圓”及其簡單應用的“微專題”復習課，取得了良好的效果，本文以此為例來談談實施“微專題”教學的幾個關鍵環節，僅供參考。

一、“微專題”課題的確定，遵循真、小、實的原則

“微專題”是立足于學生的實際學習情況而選擇的切口小、角度新、針對性強的小專題。它貼近學情，難度適中;可以進行適度拓展，激發學生潛能。“微專題”的選題不求面面俱到，而是要結合復習的目標要求，針對學生在單元復習和大專題復習中暴露出的在知識、方法和能力等方面的薄弱環節，以學生復習中的“問題”促“專題”的生成，力求解決學生學習中的“真問題”“實問題”。比如筆者設計本專題主要是考慮到以下兩點因素。

1.學生的難點。

筆者發現學生在多次的作業及考試中對隱含的阿波羅尼斯圓的關注度不是很高，從而導致這類題目答題的正確率較低。應該說，這類問題涉及數形結合、轉化與化歸、函數與方程等多個知識點及思想方法，問題本身具有一定的綜合性。

2.考試的熱點。

筆者查閱了近幾年的高考題，有關阿波羅尼斯圓的問題出現在多個省份的高考題中，如2003年北京春季卷，2008年四川卷，2005年、2008年、2009年、2013年江蘇卷，2014年、2015年湖北卷，等等。在這些題目中雖沒有直接出現阿波羅尼斯圓的概念，但經過推導、變形均能轉化得到阿波羅尼斯圓。

二、“微專題”課型的教學設計，注重知識的整合，突出以小見大

“微專題”教學關鍵在于抓住課堂內容的“主線”，以“真問題”“實問題”驅動教學，讓學生在真情境、真討論、真問題、真思考中學會學習，提出能體現核心要旨的“問題”，從而將豐富的教學內容整合成清晰的結構。

我們在對某一個“微專題”進行教學設計時，要力求找到一條能串起零散問題的“主線”，要注重揭示這些問題之間的內在邏輯關聯，這樣才能讓學生做到舉一反三，觸類旁通。要防止復習的“碎片化”，避免“就題論題”，將專題復習異化為對幾個題目的復習。

筆者分析后發現，造成學生對阿波羅尼斯圓背景判斷困難的根本原因是沒有真正理解這類曲線的本質。因此，在本專題的設計中，筆者沒有像以往的一些專題復習課那樣，過多考慮題目的綜合性或新穎性，過多注重解題的技巧訓練，而是從一組課本的習題開始，以理解阿波羅尼斯圓的本質為主線，通過回顧課本習題，引導學生回歸問題的起點，真正達到追本溯源、微中見著的目的。通過梳理學生認知結構中已有的、相對“零散”的題組，以“阿波羅尼斯圓”的概念為核心構建這類問題的本質聯系，為學生以后解決這類問題形成了一條更為清晰的“線路圖”。本專題設計了以下幾個主要教學環節來實現以上目標。

活動1：課本溯源，奠定基礎。

展示課本上的兩道題：

例1.（蘇教版《數學》必修2 P112）已知點M（x，y）與兩定點O（0，0），A（3，0）的距離之比為1：2，那么點M的坐標應滿足什么關系？

例2.（蘇教版《數學》選修2-1 P63）求平面內到兩個定點A，B的距離之比等于2的動點M的軌跡方程。

（學生思考、自主解答，具體解答過程略）

（設計意圖：挖掘課本習題的教育功能和教學價值，讓學生體會到高考題是源于課本的。此外，在此處還可以聯系橢圓與雙曲線的知識，使學生深刻理解橢圓與雙曲線的定義，熟悉其標準方程的推導過程，強化分類討論的意識，滲透類比的思想。）

活動2：特殊到一般，完善定理。

將課本習題一般化：設A，B是平面內的兩個定點，平面內的動點M到點A的距離與到點B的距離的比為定值λ（λ>0），求動點M的軌跡。

讓學生類比課本習題的方法給出解決方法。接著由教師給出阿波羅尼斯軌跡定理：

在平面上給定相異兩點A，B，設P點在同一平面上，且滿足=λ，當λ>0且λ≠0時，P點的軌跡是個圓，稱之為阿波羅尼斯圓，簡稱“阿氏圓”。（λ=1時P點的軌跡是線段AB的中垂線）

活動3：數學運用，鏈接高考。

習題1（2008年江蘇卷）滿足條件AB=2，AC=BC的△ABC的面積的最大值是______。

習題2（2008年四川卷）已知拋物線C：y2=8x的焦點為F，準線與x軸的交點為K，點A在C上，且AK=AF，則△AFK的面積為_______。

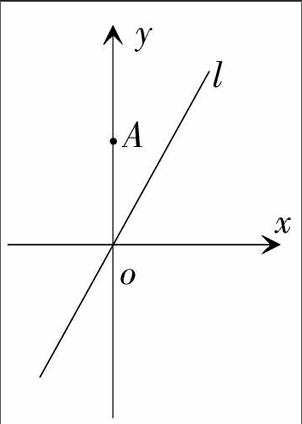
習題3（2013年江蘇卷）如圖，在平面直角坐標系xoy中，點A（0，3），直線l：y=2x-4，設圓C的半徑為1，圓心在直線l上。

（1）若圓心C也在直線y=x-1上，過點A作圓C的切線，求切線的方程;

（2）若圓C上存在點M，使MA=2MO，求圓心C的橫坐標a的取值范圍。

（設計意圖：由課本習題提煉出定理，再回到高考中體會試題出現的情境，讓學生體會這些高考題原來都是源于課本的，接地氣，易于接受。）

活動4：延伸拓展，深化思維。

在數學解題中，若僅僅滿足解出正確結果是遠遠不夠的，要善于回顧和反思，再來分析例1條件和結論：

條件：①平面上的定點O（0，0）;②平面上的定點A（3，0）;③在同一平面上動點M滿足=;

結論：點M的軌跡方程是（x+1）2+y2=4。

命題中涉及兩個定點、一個定比和動點的軌跡方程，若將這些重新組合，改變它們的邏輯次序（在已知動點的軌跡的條件下），就可以得到新的結論。

延伸1（探求定比）：已知點O（0，0），A（3，0），點M是圓（x+1）2+y2=4上任意一點，問：是否存在這樣的常數λ，使得=λ？若存在，求出常數λ;若不存在，請說明理由。

這個其實是我們經常遇到的一類定值問題：定點A，定點B，定圓C？圯定值λ。

延伸2（探求一個定點）：已知點O（0，0），點M 是圓（x+1）2+y2=4上任意一點，問：在平面上是否存在點A，使得=？若存在，求出點A的坐標;若不存在，請說明理由。

這個其實也是我們經常研究的定點問題：定點A，定值λ，定圓C？圯定點B。

延伸3（探求兩個定點）：已知點M是圓（x+1）2+y2=4上任意一點，問：在x軸上是否存在兩個定點P，Q，使得=？若存在，求出兩個定點P，Q的坐標;若不存在，請說明理由。

這個是我們常見的求定點問題：定圓C，定值

λ？圯定點A，定點B。

延伸4（探求定比和一個定點）：已知點O（0，0），點M是圓（x+1）2+y2=4上任意一點，問：在平面上是否存在不同于點O的定點A，使得為常數λ？若存在，求出點A的坐標及常數λ;若不存在，請說明理由。

此問題即為常見的求定值定點問題：定點A，定圓C？圯定點B，定值λ。

通過這幾次變式，將圓中的幾類定點、定值問題一線串之，讓學生從中看到問題的根源在于課本，認清本質，進而能做到運用自如。

三、“微專題”教學習題的選擇，突出見微知著

“微專題”教學的例題和習題選擇不要刻意求新求異，而是要立足于解決學生認知結構的真問題，應選擇部分本專題中具有代表性、可以從多個角度認識和解決、且具有深入探究價值和思維含量的問題，這類題目能夠體現解決本專題問題的核心思想與方法。筆者認為選題時應重點關注以下幾個方面的習題。

1.源于“易錯易混點”的辨析。

心理學家奧蘇貝爾說過：“影響學習的唯一的最重要的因素就是學生已經知道了什么，要探明這一點，并據此進行教學。”學生的錯題是反映學情的第一手材料，特別是學生反復做錯的一些題目，更是我們要格外關注的。此外，選擇學生作業中相關的一些易錯易混題作為專題復習的素材還有助于引導學生養成回顧與反思的良好習慣。本課例所選的阿波羅尼斯圓就是學生的易錯題。

2.源于課本習題的延伸。

高考題的源頭是教材，這是高三復習必須研究和回歸的起點和終點。當前專題復習中對一些知識和方法交匯處的綜合題、高考題關注得比較多，而對課本的習題關注得不夠。課本的習題都是經過專家反復推敲，最能反映相關數學知識和方法應用的典型題目，歷屆高考試卷中來自課本原題或改編題的考題比比皆是。因此，課本的習題理應成為復習重點。本課例的背景就是來源于課本，由課本題展開并延伸拓展，讓學生對高大上的高考題不再畏懼。

3.源于典型的高考題。

選擇一些典型高考題作為復習題有助于我們在復習中準確把握高考的命題方向，克服復習中出現一些偏題、怪題。但在使用高考題時要注意和復習的專題相吻合，不可生搬硬套，沖淡復習的主題。本專題中的“活動3：數學運用，鏈接高考”中的習題均是選自近幾年的高考題，讓學生體會阿波羅尼斯圓在高考題中的呈現形式。

四、“微專題”復習課的教學，注重課堂的生成

課堂教學是預設和生成的有機融合，預設是為了更好地生成。“微專題”復習課的教學中，更要給學生足夠的思考時間，讓學生回顧和梳理問題解答的過程，體會它們之間的本質聯系，最好讓學生自主生成串起這個專題的一條“主線”，進而在頭腦中形成對一類問題的本質認識。因此，“微專題”復習課的重點應放在學生對解決本專題問題的一般思想方法的生成上，而不是在單個題目的具體解法上，否則，這樣的專題教學會異化為同類題的綜合訓練，起不到專題復習的效果。例如在本專題的教學中，筆者將教學的重點放在以下兩個方面：一是幫助學生自主構建阿波羅尼斯圓定義的基本方法，二是讓學生體會函數與方程的聯系、數形結合、轉化與化歸等數學思想方法。

以上是筆者對“微專題”在高考數學復習中的一些實踐和思考，由于“微專題”是立足于具體的學情、教情和考情而靈活設置的專題，沒有現成的復習資料可以照搬，對如何提高這種形式的復習課的效果、還有待各位專家和同仁不斷研究和實踐，以更好提高高考數學復習的有效性。

注：本文系江蘇省教育科學“十二五”規劃2015年度立項課題“高中數學‘微專題教學的實踐研究”（課題編號：D/2015/02/165）的階段研究成果之一。