試論高職高專高等數學中常用的求極限方法

試論高職高專高等數學中常用的求極限方法

許 霞

(新鄉職業技術學院，河南 新鄉 453000)

摘要：極限是高職高專高等數學的重要知識點之一。為破解困難，提高學習效率，應該熟練掌握不同的求極限方法，并根據題目靈活應用，促進解題效率提高。結合高職高專數學實際情況，介紹幾種常用的求極限方法，希望能為學生學習提供啟示與參考。

關鍵詞：高職高專；極限；解題方法；四則運算法則

doi:10.3969/j.issn.1674-6341.2015.05.045

中圖分類號：G642.4文獻標志碼：A

收稿日期：2015-06-26

作者簡介：許霞(1980—)，女，河南開封人，碩士，講師。

研究方向：數學教育。

0引言

極限是高職高專學習的重要內容，也是最基本、最核心的概念之一，幾乎貫穿于高職高專數學教學，為學生和任課教師所普遍關注和重視。但極限知識學習比較難，一些學生往往未能有效掌握求極限的方法，難以根據不同題型熟練應用解題方法，制約了學生學習效率的提高。因此，應該加強訓練，熟練掌握和應用各種方法，提高學習效率。

1利用極限四則運算法則求極限的方法

極限計算過程中，四則運算法則是求解的重要方法，學生學習和解題過程中應用比較普遍。通常在解題中，結合不同題目類型，可以直接或間接應用該方法。

(1)直接利用四則運算法則。從簡單函數的極限出發，分析和計算較復雜函數，得出結論。利用四則運算法則計算時，前提是存在極限，且分母極限不為零。如果不滿足這個條件，就不能直接利用該方法求極限。

(2)間接利用四則運算法則。分母極限為0，或分子、分母極限為∞，為順利得出計算結果，需要對運算法則間接利用，通常又分為以下方法。

①有理分式可將分子、分母分解為因式，約簡分式后取極限。

解：令x=y12，當x→1時y→1得：

解題時，選取冪指數等于已知函數所含根指數的最小公倍數，替換后可去掉根號，并消去因子(x-1)。

②極限式含有根式，有理化并消去不定性，再取極限。

③當x→∞，分子、分母極限為∞，用分母最高次冪去除分子分母，再取極限。

④極限計算間接應用四則運算法則時，除了上述三種不同方法外，利用無窮大與無窮小間的關系，也能順利求出極限值。但不管采用哪種方法，首先需要根據題目實際情況合理選用，并按步驟做好每項計算，最終求出極限值。

2利用無窮小的性質求極限的方法

利用無窮小性質求極限也是常用方法，有界函數與無窮小的乘積就是無窮小，這是解題中需要重視的問題，以避免出錯，從而求出正確的極限值。

3利用兩個重要極限求極限的方法

在求極限過程中，根據題目實際情況，要熟練利用以下兩個極限，順利求出結果，以達到順利解題的目的。

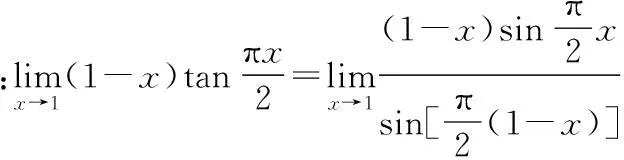
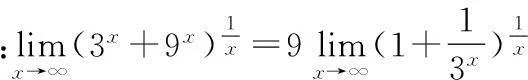
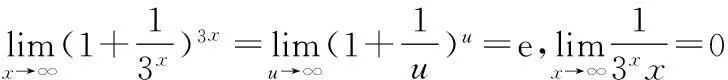
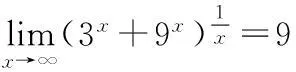
4利用等價無窮小代換求極限的方法

求兩個無窮小之比的極限時，分子分母用等價無窮小代替，通過替換之后，使計算變得更加簡單，簡化計算流程，從而正確求出極限值。

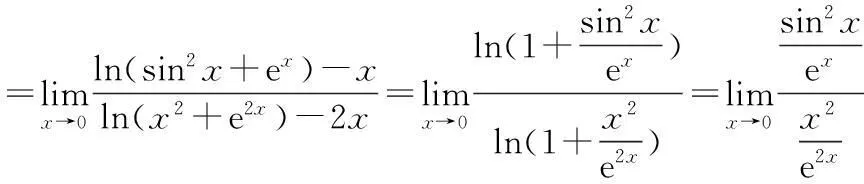
5利用函數連續性求極限的方法

連續性是函數的重要性質，求極限時合理利用能簡化計算流程，實現順利解題的目的。函數在定義區間內各點處是連續的，對于函數f(x)，若x0是它定義區間內一點，要求f(x)極限，只需求f(x0)即可。

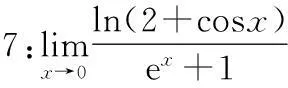
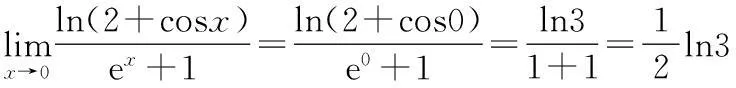
6利用羅比塔法則求極限的方法

法則計算和分析，解題過程中先將“非零因式”分解出來，再進行求解。

對于1·∞、00、∞0型不定式，先對它們取對數，使之成為0·∞型不定式，設：y=[f(x)]g(x)，則：lny=g(x)lnf(x)，從而[f(x)]g(x)=eg(x)lnf(x)，當x→x0時，g(x)lnf(x)是0·∞型不定式。

7結語

極限是高職高專數學重要內容。不同方法有不同特點，適用不同題型，但這些方法都能解答極限學習中遇到的計算問題，幫助學生解答疑惑，解決困難。有些極限計算需綜合應用多種方法，學生在日常學習過程中要全面考慮，熟悉每種計算方法，能根據不同題目靈活應用，從而促進學習效率的提高。

參考文獻：

[1]黃阿娜.高職高數一元函數極限的求法綜述[J].職業教育,2014，(4)：161.

[2]李文鋼,徐霖.略談求函數極限與數列極限的幾種常用方法[J].安慶師院學報：自然科學版,2006，(5)：93—95.

[3]蘇文珣.高職高專教學中求函數極限的幾種方法[J].重慶電力高等專科學校學報,2008，(2)：53—56.

[4]陸忠敏.高職高專中常用的求極限的方法[J].赤子,2013，(7)：182—183.

[5]李愛真,王秀梅.淺談高職高專中高等數學與中學數學教育的銜接[J].河南機電高等專科學校學報,2006，(1)：110—111.

[6]單傳偉,生靜.高職高專高等數學中求極限運算所適用的常用方法[J].南昌教育學院學報，2012，(2)：119—120.

責任編輯：柴造坡