用文化的養分滋養課堂

顧衛華

[摘 要]數學是人類文化的重要組成部分。發掘數學學科特有的文化意蘊，帶領學生經歷“再創造”的文化軌跡，可以讓數學學習變得更加生動、豐滿、厚實。以“三角形面積計算”教學為例，談談如何用文化的養分滋養課堂，建立起基于“文化”開掘、傳承、發展、創新的教學思維。

[關鍵詞]數學學習 數學文化 三角形面積計算

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2015）35-008

著名特級教師張乃達先生認為，“數學是在數學文化背景下的思維活動”，“思維與文化，集中地體現了數學教育在提高學生素質教育中的兩項要素，所以也是現代數學教育的兩個重要方面”。個人以為，作為數學教育的兩翼，思維與文化并不是分離的，而是有機統一體——文化靠思維來打造和提煉，思維就在文化中，思維是數學文化的重要組成部分。本文以“三角形面積計算”為例，談談自己在這方面的思考與實踐。

研讀

多年來，小學教材中關于圖形面積計算的學習，有一個比較穩定的邏輯順序：長方形面積計算——平行四邊形面積計算——三角形面積計算——梯形面積計算——圓面積計算。“三角形面積計算”是這個鏈條的中間環節，因而教材編排思路是用“兩個完全一樣的三角形”拼成一個平行四邊形，三角形的底等同于平行四邊形的底，高等同于平行四邊形的高，面積等同于平行四邊形面積的一半，從而推導出三角形面積計算公式。這樣的編排，體現了循序漸進、螺旋上升、新知建立在舊知之上的科學原理。

考慮到學生的認知規律，為更好地體現圖形直觀的新課改理念，現行教材從一年級下冊開始，對兩個完全一樣的三角形能拼成一個平行四邊形或者一個平行四邊形能分成兩個完全一樣的三角形進行了多次鋪墊（圖1為蘇教版二年級上冊“平行四邊形的初步認識”中的習題），以期學生能從平行四邊形面積推導時的“割補”順暢地轉換到憑空再借一個一樣的三角形來“拼”。

圖1

客觀地講，教材中的這種變化基本上還是在原有的編排框架之中把“戲份”做得更加充分而已，但只增加了“長度”而未能增加“厚度”。

思考

翻開厚厚的數學發展史，我們發現，多邊形的面積計算都來自對土地的測量。譬如古埃及的紙草的第三部分講述了如何確定正方形、矩形、三角形、梯形以及能分割成這些形狀的圖形的土地面積。隨后，人們又發現任意的多邊形可以分割成多個三角形來求出面積。正因為土地的形狀不太可能出現平行四邊形，所以在歷史上，起初的三角形的面積計算壓根就和平行四邊形無關。顯然，教材的安排是出于對學生認知難度考慮而作出的一種優化，而優化往往忽略了發展的曲折。

再從數學自身發展中挖掘這一內容的學科魅力。數學家發現三角形面積計算公式后，有個難題擺在了前面：“不知道三角形高的情況下怎么求三角形的面積。”而海倫公式的發現解決了這個難題（注：利用三角形三條邊的長度來求三角形的面積）。很明顯，如果不按照教材設置的指向，而是讓學生像數學家一樣思考、爭論、探索，那學習是不是有另一番風景呢？但是，在課堂重現歷史發展的腳步，還原三角形面積計算的另一種推導，無論從自主發展，還是多種方法的創新思維來說，都是有價值的，同時也是有難度的。

以往的教學經驗告訴我們，學生在沒有自習書本的情況下，受前一課平行四邊形面積計算公式推導的影響，還是能想到“割”的，但往往想不到怎么去“割”。有個以往無法避免的難點在于小學五年級的學生還不知道什么是“中點”。

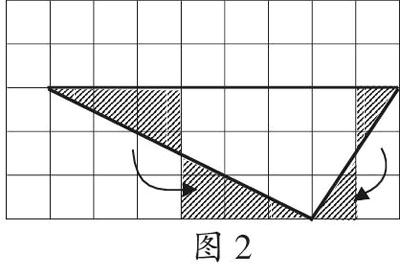
他山之石可以攻玉！《小學教學參考》2015第4期查人韻老師的嘗試給了我靈感的火花。從圖2可以看出，借助方格圖，可以繞過“中點”這個坑，從而順利還原古人的思路，從而實現真正多角度的自主探究。

實踐

我的教學分三個板塊進行。

第一板塊“開門見山”，提問“三角形的面積可能和哪個圖形有聯系？”由于有上一課的經驗，學生很容易回答出“長方形或平行四邊形”。先規定探究方向，節省時間。

第二板塊直接出示先學單（格子圖上有3種三角形：底4高6的直角三角形，底6高4的等腰三角形，底6高5的一般三角形，每種圖形有三個，期待每個學生有不同的方法），讓學生探究三角形的面積是多少。

在開放的探究環境中，真正地體現了思維的差異，方法的多樣。數格子的學生在真心實意地數格子，而不是教師指點的“還可以數格子”;對于直角三角形，有學生一下子想到了“拼成一個長方形”……因為借助了格子圖，學生直觀的思維能力得到了充分地應用，精彩的想法遠遠超過了教師的預期。可以說，這里的轉化來自學生的直覺判斷，并不嚴謹，但是卻飄逸靈動。

探究后全班交流：1.自評互評，這個方法好在哪里，不好在哪里？引導橫向比較，發現優點和不足。2.比較算式，為什么有4×6÷2，又有3×4？怎么看上去算式不一樣？創設困惑，讓學生發現一般的公式，其實3×4就是6÷2×4，雖然看起來不一樣，但本質是一樣的。因為有了充分的探究，學生真正是帶著自己的思考，聆聽別人的想法，合作探究完全不是“做做樣子”。

第三板塊介紹“劉徽著《九章算術》中三角形面積的圖例（如圖3）”，指出：“我們比數學家更厲害，不僅解決了等腰三角形的面積問題，還推廣到了一般三角形呢！”

學生發現自己的想法和數學家一樣，積極的情感體驗帶來深刻的自我認同，“我能行”在學生的心中生根發芽！

啟示

數學課程標準在“前言”部分提及：數學是人類文化的重要組成部分。作為人類文化的數學，應該充分挖掘數學在產生、發展、豐富、壯大的過程中人們所經歷的曲折過程、突破常規的超越、偉大的創造等精髓。讓學生像過去的人們、像數學家那樣去經歷數學的發生、發展過程，會讓學生更多地體會到數學的“溫情”、傳奇、美妙與偉大，這樣的數學學習才會印象深刻，令人難忘。

當然，數學文化具有豐富的內涵和多樣的姿態，用張齊華老師的話說，就是“探索過程中的執著與堅韌，論證過程中的務實與謹嚴，數學規則推導過程中的理智與自律，數學創造過程中的開拓與超越，甚至于耐心、責任感、敬業品質、民主精神等都具有獨特的‘教化功能，正是這些，見證著數學更為深沉的文化力量，使數學可以超越知識本身，找尋到更為樸素、更為豐富，也更為動人的內涵”。

有人說，文化的內核是“化人”。用文化的養分滋養數學課堂，文化熏陶終究會轉化為文化自覺，讓每一個孩子既成為文化的守護者，還成為文化的創造者。

（責編 金 鈴）