基于APOS理論的函數單調性概念教學設計

劉吉順

摘 要：APOS是美國學者杜賓斯基提出的關于數學概念學習的學習理論，主要是在傳統教學的基礎上，通過APOS理論設計函數的單調性概念教學，從而制作出成熟的教學方案，為函數概念教學提供理論依據。

關鍵詞：APOS；函數單調性；教學設計

隨著教學理論的發展，諸多新穎的教學設計融入當前的教學過程中來，其中，APOS理論能夠通過階段模式多快好省地解決函數單調性等數學難題，是行之有效的教學設計方法，值得推廣應用。

一、APOS的含義

APOS是美國學者杜賓斯基提出的有關數學概念學習的學習理論，其認為，學生學習數學需要經過四個階段，即操作階段、過程階段、對象階段以及圖式階段，該理論不僅表明學生的學習構建過程，還對構建層次分別說明。

操作階段主要是促使學生明確問題概念和背景之間的關系；過程階段主要是學生概括思考的過程，通過思維內化從而明確概念性質；對象階段是經過明確概念本質，將其予以壓縮，并且賦予形式化的符號及定義，從而演變為思維對象，從而在學習過程中創建新活動；圖式階段是在長時間學習后予以完善，剛開始的圖式包括符號、定義以及特例等抽象過程，隨后建立起圖形、規則與其他概念的關聯，從而逐漸演變成綜合的心理圖式。

二、函數單調性概念數學設計

（一）設計說明

作為函數章節中最重要的性質——單調性，不僅是學習的重點，更是學習的難點，由于單調性定義較為晦澀難懂，因此，對于學生而言學習并不輕松，學生認知函數單調性的困難主要包括：（1）函數圖像的升降被函數符號代替，將直觀轉變為抽象學生并不能夠完全適應，極難把握。（2）證明函數單調性必須應用單調性定義，如果對定義沒有一個深刻的認識，將會致使學生在解題過程中存在諸多問題。

（二）教學過程設計

1.操作階段

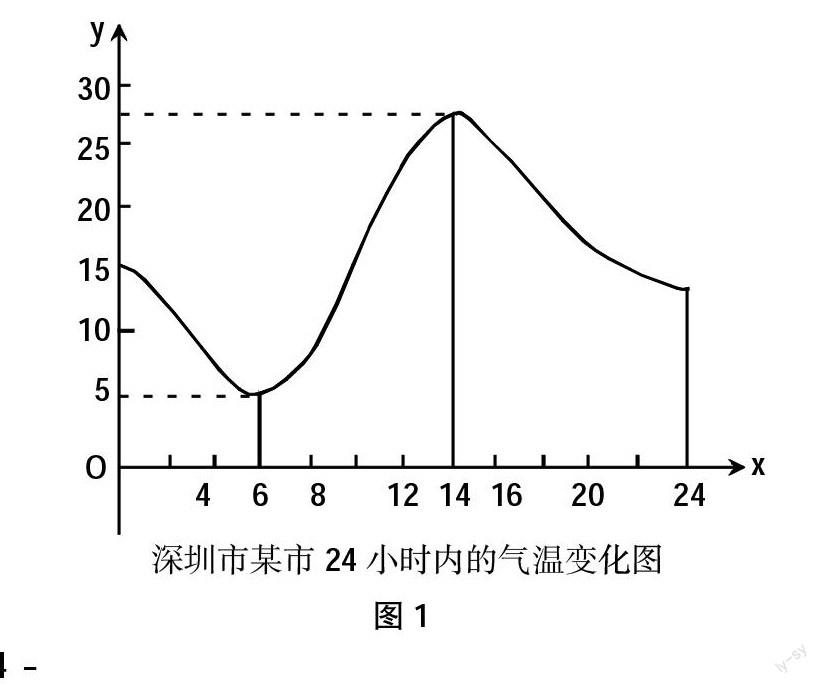
教師需要創造問題情境，對思考問題進行模擬，比如深圳某市24 h氣溫變化圖，如圖1所示：

教師需要引導學生看明圖中所給的信息，并且總結信息，進行思考。

例如，教師詢問：（1）該圖顯示哪日的溫度最低？哪日的溫度最高？（2）某日的某時的具體氣溫能否看出？（3）哪些時間段溫度有上升的趨勢？哪些時間段有下降的趨勢？

[設計意圖]通過簡單的氣溫變化圖，對函數的單調性予以簡要說明，比如溫度趨勢對應函數的遞增和遞減，定位為y隨著x的減小而減小以及y隨著x增大而增大。

2.過程階段

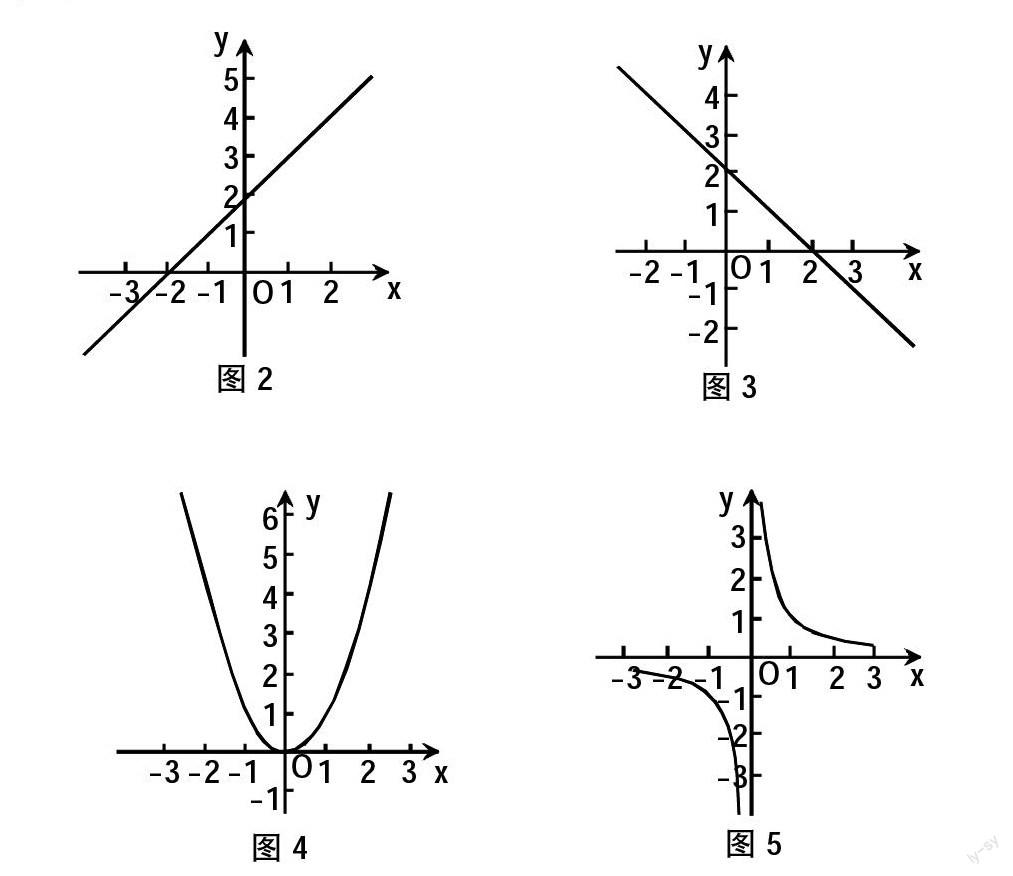
過程1：將函數y=x+2（如圖2），y=-x+2（如圖3），y=x2（如圖4），y=（如圖5），對其自變量變化過程中函數值的變化規律予以分析。

在向學生說明圖像單調性過程中，必須強調是處于某個區間的單調性，從而促使學生明確單調性的局部特征，不得存在概念盲點。

過程2：用淺顯易懂的話講明增函數及減函數。

[設計意圖]通過直觀的表達出單調性的概念，從而實現描述性認知的目的。

過程3：直觀到抽象

如何證明f（x）=x2在區間[0，∞）是增函數？

（1）任意在區間[0，∞）中取兩個值，比如3和4，由于3<4，因此f（x）=x2在區間[0，∞）是增函數。

（2）根據（1）算法選取若干組予以驗證，結果均滿足條件，因此f（x）=x2在區間[0，∞）是增函數。

（3）選取任意數值x1，x2∈[0，∞），x2>x1，又因為x22>x12，所以

f（x）=x2在區間[0，∞）是增函數。

教師詢問：怎樣通過精準的數學符號對函數單調性予以定義？

師生共同探討，從而明確增減函數的定義，并且強化學生對增減函數的理解。

[設計意圖]強調自變量在區間的任意性，并且對函數加以驗證，信息分析數學符號的嚴謹性。

3.對象階段

判斷命題真假。

（1）y=，由于f（-2）

（2）如果f（x）滿足f（3）

（3）假如函數在（2，4]區間和（4，6）區間均為增函數，那么函數f（x）在區間（2，6）也為增函數。

[設計意圖]通過反例的形式強調單調性定義域中存在的諸多問題。

4.圖式階段

證明函數在區間是增函數。

[設計意圖]對證明函數單調性的步驟進行歸納：設元、作差、變形、斷號、定論。

三、注意問題

操作階段：在設置問題情境時需要適宜經典，確保行之有效。

過程階段：通過思維深入引導，有針對性地升華“對象”，教師在此過程中詢問“是什么”以及“為什么”“怎么樣”等，并且留給學生足夠的時間去思考探索。

對象階段：對概念的本質特征深入了解，要求學生能夠將概念抽象化，逐漸形成心理表象，并且加深對概念的認知和理解，在教學過程中通過反例、變式引起學生思考，并且對其不斷優化

調整。

圖式階段：通過多次操作將學生“對象”層次轉變為“圖示”層次，并且通過多種方式促使學生理解“對象”，不能一蹴而就。

總而言之，基于APOS理論，能夠有益于函數單調性的概念教學，而且能夠在多學科多領域中融會貫通，值得推廣應用。

參考文獻：

[1]高波.基于APOS理論的職高數學概念課教學設計探析：以《函數的概念》為例[J].考試周刊，2014（11）：45-46.

[2]賀明榮.基于多元表征理論的函數單調性教學設計[J].上海中學數學，2013（12）：1-3.

[3]孟世才.基于APOS理論的中學函數概念的教學研究[J].教學與管理：理論版，2011（21）：95-96.

編輯 韓 曉