關于課題學習最短路徑問題的探究
李尉連

【摘 要】課題學習在數學課標中指出是學生第三學段“實踐與綜合運用”體系的重要內容,其特點包含:主體性、開放性、探究性、創新性和綜合性等,促使學生成為課題學習課堂的主體,提高學生創新、探索思維,加固學生對知識的掌握,教師依據所教學的內容進行有科學性、合理性地整合,確立明確的課題教學目標,有效施展各種教學方法,提高學生對知識的運用,培養學習相應課題解決的技巧,檢驗知識教學的效果。
【關鍵詞】課題學習;最短路徑問題;實施;交流
序言
最短路徑問題的教學在初中教學中出現有幾種類型,頻繁出現的主要在幾何與函數知識點教學方面,以學生能力提升為主,教師應當在選擇課題時注意此點,采用便捷、靈活的計算方法和技巧,優化教學方法,提高學生解題的效率,培養學生數學邏輯思維能力。
1.課題學習原則
課題學習屬于新穎的學習方式,課題學習課堂上教師需要對教科書或者是相同類型的課題、題型進行有效整合,通過教師的教學引導,綜合運用各種解題方法對課題進行解決,積累更多課題知識,提高自主探究能力,拓展學生學習交流,引發更多學習創新方法,課題學習有關特征主要有四種:主體性,課題學習可以充分體現出學生在學習的過程中是要通過合作討論、自主探索的學習方式,才可以在解決數學問題有清晰的解題步驟和思考思維,以問題作為出發點,然后主動思考問題,體現了學生主體地位突出;探究性,課題學習教學需要教師引導學生對問題進行探究,絕不可直接解答題目反而遏制了學生探究思維的開發,必須要體現課題學習的探究性;綜合性,課題學習所涉及的內容比較廣泛,如果是在初中三年級的話,學習最短路徑問題就會涉及到整個初中數學知識體系,包括的范圍廣,或者還接觸到其他學科中去,體現課題學習的綜合性強的特點;開放性,課題學習不局限與教材的內容,學習本來就具有融會貫通的思維能力,沒有持久不變的題目,只有永恒的邏輯思維,當遇到相類似的題型,就需要學生使用解題技巧和數學理論知識結合起來,教師亦當如此。
2.強化對“課題學習”理論的認識的理解
教師在進行“課題學習”的課堂之前,幫助學生對各個類型的知識點進行回顧,把相關的數學概念和定理整理歸納好,思考各個類型知識點和問題的解決途徑和技巧。同時,教師也需要加固課題學習所涉及的數學知識點和教學的相應技巧與教學方法,充分做好備課工作,深刻認識到“課堂學習”的重要教學理念和實際的教學目標,做好課堂的教學規劃和改善課堂教學流程。
3.規劃“課題學習”教學方案
此次“課堂學習”的教學內容是關于初中數學最短路徑的問題,教師需要根據學生所學過的知識內容進行規劃后課堂教學的方案,分配好各個知識點的最短路徑問題在課堂上利用的時間,知識點的難易程度、解題方法和教學方式會決定所耗費的時間長短。關于最短路徑的問題教師首先收集好典型且具有意義性的題目,并且了解如何進行解答。例如教師可以從螞蟻沿正方體、長方體、圓柱、圓錐外側面吃食,其原理是線段之和最短的問題或者是數模、函數等方面進行收集相關的數學題目,此外,在題目中還需要對該知識進行拓展,或者構思不同方式的題目,拓展學生思維的界限,教師還應強調由易到難的教學觀念。
例如:
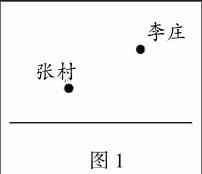
問題一、如圖1,要在河邊修建一個水泵站,分別向張村、李莊送水,水泵站修在河邊什么地方可使所用的水管最短。
圖1
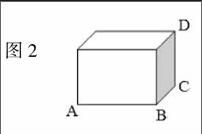
此問題的要求就是要在直線上找到一個點,這一點要使得直線同側的兩個定點到這點的距離之和要達到最短,此題利用到“兩點間的所有連線中,線段最短”的理論來進行論證求解。除了這一題外還有其他相同類型的題目比如:螞蟻的爬行問題,如圖2是一個長方體木塊,已知AB=5,BC=3,CD=4,假設一只螞蟻在點A處,它要沿著木塊側面爬到點D處,則螞蟻爬行的最短路徑是多少?
圖2
這都屬于最短路徑的數學題目,涉及到幾何體的內容,需要拆開的方式來求證。
問題二、數學知識點不僅僅只有這點,還有關于幾何方面的知識都有最短路徑的探究:
如圖3,AB是⊙O的直徑,AB=2,OC是⊙O的半徑,OC⊥AB,點D在弧線AC上,弧AD等于2倍的弧CD,點P是半徑OC上的一個動點,求AP+PD的最小值是多少?
圖3
這類型的題目需要結合到幾何定理知識來求解。
教師在進行“課題學習”之前就需要對這些類型的題型完全把握好,分析幾何型和數形結合的問題,理清解題的過程,貫穿到哪些方面的數學定理、概論。結合到題目的難易程度或者知識點范圍,可以規劃幾個課時才可以解決,制定明確的課堂流程。
4.利用教學方法促成“課題學習”教學
教師進行改善教學方法,需要考慮到“課題學習”的主要特點來制定相應的教學方法,就從它有主體性的特點來思考。教師可以展開小組合作討論活動,對最短途徑問題進行探索,為學生提高情境教學的環境,提高學生課題學習課程的興趣,培養學生探索思維,創新思維。例如在“問題一”中的第二類型的題目上展開小組討論活動,由于問題難度不算高,教師可以一兩人為一小組,提倡學生利用上現有制作的數學模型展開討論,可以把制作好的長方體標記好有字母的標記,讓學生進行思考探索,學生在探索思考過程中,加上動手的操作,就可以理解到如何進行解決問題。從小組討論的教學方式來說,極好地體現了“課題學習”教學的有效性。此外,教師還應該采用數形結合法來教學,圖像的表達可以把抽象的數學條件,誘導出形象的圖像,加快學生解題速度。
結語:綜上所述,數學問題萬變不離其宗,所有題目或者題型的變化,都可以找到問題的突破口,結合數學理論知識就可以把問題解答,課題學習的關鍵作用使得學生在學習過程中對知識點的回顧,加深對知識的理解,同時可以培養學生的創新思維和探索精神。
【參考文獻】
[1]葉瀾.《“新基礎教育”探索性研究報告集》,三聯書店,1996年版
[2]戴向陽.動點下的線段最值解法探微.中學數學教學參考,2014(3)
[3]朱啟州,張興俠.一道課本例題的教學探討.中學數學教學參考,1999(4)
[4]李萬富.空間圖形的“最短路徑”問題[J].今日中學生,2006年30期

