完整建構學生知識體系 實現高效課堂
劉穎
摘 要:合理安排教學內容,深入領會教材的編排意圖,引導學生經歷知識的形成過程,探究規律產生的科學依據,尋找規律間的內在聯系,完整建構學生知識體系,是實現高效課堂的重要環節。
關鍵詞:完整建構;高效課堂;課堂回顧
在高效課堂的研討活動中,本人執教了“找次品”一課,以“找次品”這一操作活動為載體,讓學生通過觀察、猜測、試驗等方式感受解決問題策略的多樣性,在此基礎上,通過歸納、推理的方法體會運用優化策略解決問題的有效性,感受數學的魅力。以下摘錄其中兩個片段進行理性分析和反思。
【課堂行為分析】
《義務教育數學課程標準》指出:“有效的數學學習活動不能單純地依賴模仿和記憶,動手實踐、自主探索與合作交流是學生學習數學的重要方式。”著力讓學生通過參與有效的實際操作、觀察比較概括出“找次品”的最佳方案。在自主建構知識的基礎上,建立了“猜想—驗證—反思—運用”的教學模式。上完后,總覺得一節課被分成了兩個孤立部分(待測的物品是“3的倍數的”和“不是3的倍數的”),這兩部分能否和諧聯結?基于以上思考,下面就從“完整知識建構”方面談一談。
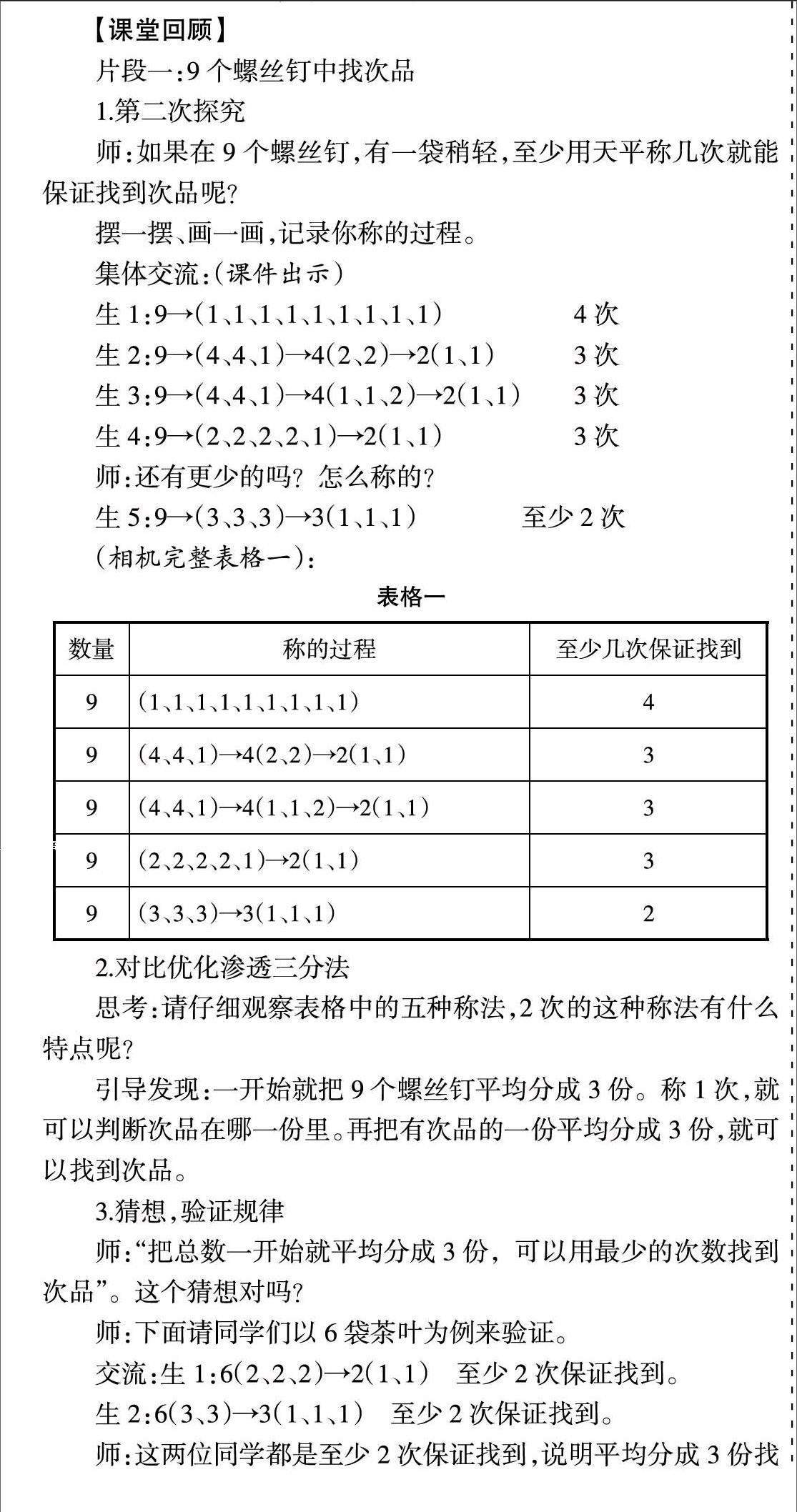
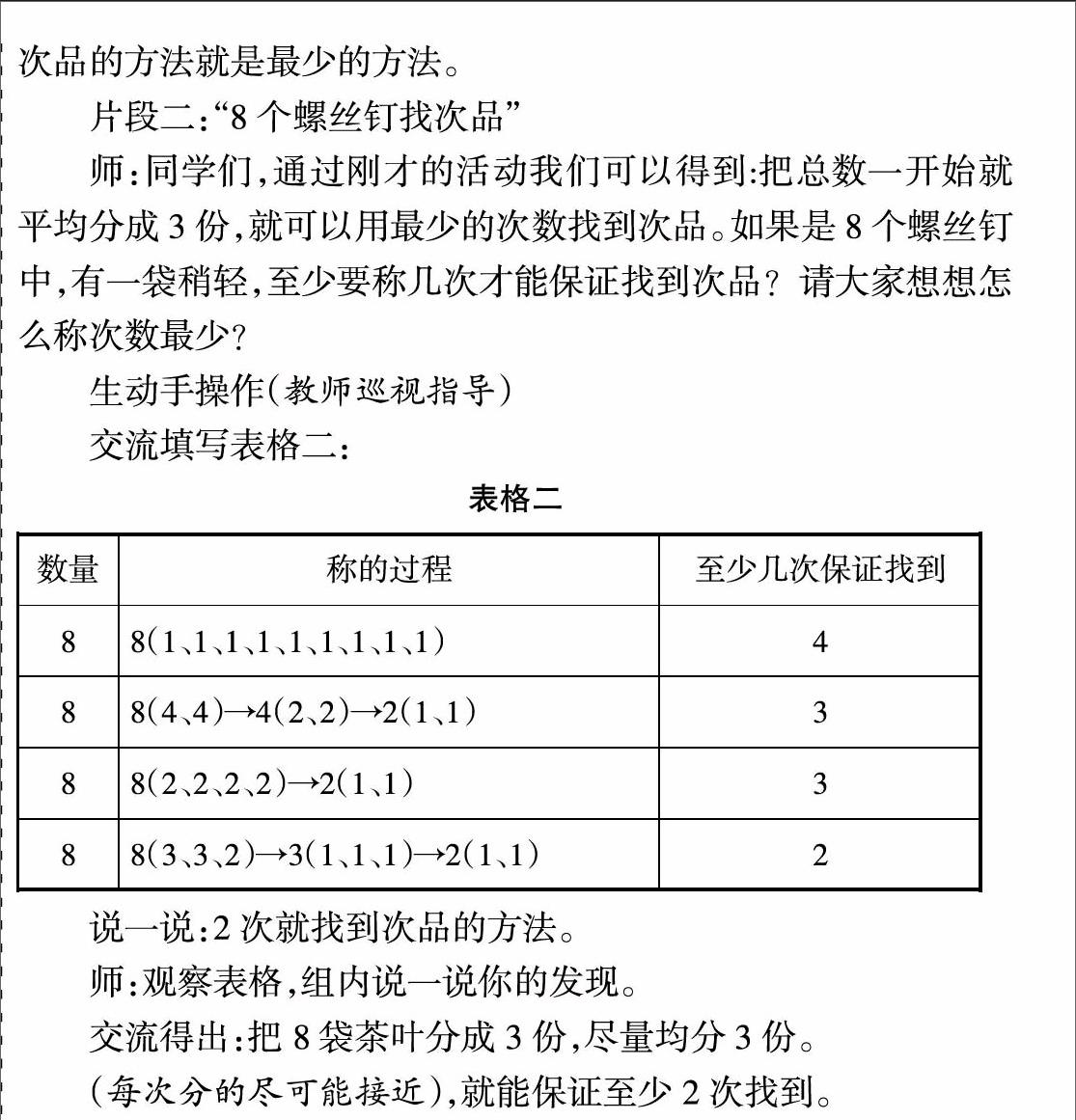
本節課注重“數學化”的過程,即由具體到抽象,由特殊到一般的數學分析模式。先讓學生探討待測物品為2個螺絲釘、3個螺絲釘、5個螺絲釘、9個螺絲釘時怎樣找次品,并羅列出各種解決方案,且各有側重。如,2個待測物品引入用天平稱的方法,借助肢體語言,認識天平的平衡原理;研究3個待測物品,通過擺一擺的方法,引導學生推理,體會“保證找到”的意義;研究5個待測物品,僅要求學生說出找次品的方法,不需要進行規律總結,讓學生感受解決問題策略的多樣性,并學會用數學的方法記錄;研究9個待測物品,從這些方案中尋找規律,總結、提煉出一般方法和優化策略,使學生經歷由多樣化過渡到優化的思維過程。但由于本節課把2課時知識融在一課時進行,內容多,時間緊。有些知識點只是一帶而過,不能進行深入探討。如:“9個螺絲釘中找次品”得出均分3份,保證至少找到的原因,是“第一次盡可能多的排除。”并沒有進一步深入探究排除了多少?其他方法第一次又能排除多少?學生的思維僅僅停留在這一層面。再如,在研究“8個螺絲釘中找次品”這一環節,就更為倉促,學生匯報完幾種情況后,比較得出:“盡可能均分3份,保證至少找到。”
學生是否真正理解“均分3份和盡量均分3份的道理?為什么這樣就能保證找到次品次數最少?兩者之間是否有聯系?”如何讓學生知其然,知其所以然。因此在研討的基礎上增加了一個“深入理解”的環節,再次引導學生認真觀察表格一和表格二,仔細比較稱的過程,不難發現:3的倍數可以用3n來表示,不是3的倍數的就可以表示成3n+1或3n+2。從而推出:
當3n時:n n n→一次就能排出三分之二
當3n+1時:n n n+1→一次也能排出接近三分之二
當3n+2時:n+1 n+1 n→一次就能排出三分之二還多
使學生明白“均分三份”和“盡可能分成三份”,為的就是一次能盡可能多地排除,保證次數最少的道理,達到知識之間的和諧聯結,完整建構學生的知識體系。
【總結歸納】
總之,合理安排教學內容,深入領會教材的編排意圖,引導學生經歷知識的形成過程,探究規律產生的科學依據,尋找規律間的內在聯系,完整建構學生知識體系,是實現高效課堂的重要環節。
參考文獻:
鄭毓信.“找次品問題”與數學思維[J].小學數學:教學版,2011(17).
?誗編輯 薛直艷

