“勾股定理”的教育價值與教學策略分析

嚴曉冬

[摘 要] 每一個知識內容都有其內在的教育價值，將勾股定理置于數學知識體系和文化價值系統中進行分析，找到勾股定理與其他知識內容之間的橫向、縱向聯系有助于課堂教學策略的優化，幫助學生在習得知識的同時發展數學思維和學科素養.

[關鍵詞] 勾股定理；直角三角形；關系；問題

勾股定理是初中數學教學的一個重點、難點問題，筆者在教學設計中首先從其內容出發，闡述勾股定理的教育價值和學科作用，接著就該節內容的課堂組織策略進行分析.

勾股定理的內容

搞清楚勾股定理的內容是有效實施教學的前提，具體的可以從代數和幾何兩個角度進行敘述.

1. 代數角度的敘述

文字表征：直角三角形兩直角邊的平方和等于斜邊的平方.

符號表征：a2+b2=c2（a，b和c分別表示兩直角邊和斜邊）.

2. 幾何角度的敘述

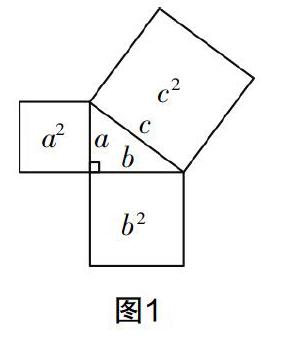
文字表征：一個直角三角形，以兩直角邊為邊的兩個正方形的面積之和等于以斜邊為邊的正方形的面積.

圖像表征：如圖1所示.

勾股定理的教育價值

一個知識的教育價值是多方面的，對于勾股定理這個內容，其教育價值和學科價值有如下幾個方面：

1. 文化價值

從數學史上看，人們發現勾股定理、驗證勾股定理及應用勾股定理的過程蘊涵著豐富的文化價值，我們在教學過程中注重這些數學史、研究過程，有助于激發學生的數學學習興趣，在學習過程中體悟其存在的意義和實際價值.

2. 學科價值

從勾股定理的內容來看，其同時具有代數和幾何的雙重特征，是初中數學階段幾何與代數之間問題研究的一個重要橋梁，從勾股定理的證明方法來看，“演繹法”“變換法”和“代數法”三種方法教給學生，尤其是學生通過學習變換法（拼圖法），能夠幫助他們感受和理解運動與變換.

知識的教育價值不僅僅表現在概念和規律本身，在教學中還應該滲透知識探究和被發現的過程. 勾股定理的發現、驗證整個過程均蘊含著豐富的、可滲透的思維素材，和學生一起探索和證明勾股定理，能夠豐富學生的學習經驗，感悟數學學習和不斷探索未知的價值：

（1）學生在探索過程中，探究圖形基本元素之間的關系、幾何結構，而這一過程必然涉及空間推理和演算，從中學生能夠感悟到數形結合的思想方法，同時體會推理和證明的力量.

（2）學生通過勾股定理的探索和證明，會自然而然地形成一種意識，那就是要了解我們生存的空間，必須要學習更多的數學工具，并合理地應用.

勾股定理知識系統內結構分析

數學知識具有較強的系統性和完整性，置于知識系統中，勾股定理與其他知識有著怎樣的聯系，學生在學習進程中又有怎樣的連貫性呢？

1. 知識間的橫向聯系

《勾股定理》在初中階段與其他數學知識內容密切聯系，如無理數、三角函數、方程、四邊形、圓等知識.

2. 知識間的縱向聯系

從學生的學習進程來看，初中之前，學生在小學階段對三角形的三邊關系有了一個初步的了解：兩邊之和大于第三邊；步入初中，學習勾股定理內容前，學生通過探索也對直角三角形的性質有了一定的了解：“斜邊上的中線等于斜邊的一半，30°角所對直角邊是斜邊的一半. ”

那么，勾股定理在這里又有怎樣的作用呢？學習了這一內容后，學生可以進一步從邊的角度來定量地刻畫直角三角形的特征，由此進一步深化學生對直角三角形的認知.

學生從初中步入高中階段后呢？勾股定理有沒有其價值呢？學生在高中將要繼續學習任意三角形中邊長與角度之間的數量關系，在學習和理解正弦定理和余弦定理時，需要用到勾股定理，可以將勾股定理視作為余弦定理的一種特殊情況.

整個學習過程對直角三角形邊角的關系，是從定性到定量，從一般到特殊再到一般的思維進程.

幫助學生學會勾股定理的教學策略

如何幫助學生學會勾股定理呢？

1. “探索→猜想→證明”法

筆者發現當前有部分教師在和學生探究勾股定理時采用的方法是：首先讓學生測量直角三角形三條邊的長，接著要求學生猜想三條邊長之間存在怎樣的數量關系，在學生猜想出三邊之間的平方關系后，再證明勾股定理.

這樣的方式有怎樣的缺點呢？

筆者曾經也嘗試過這種方式，看似邏輯性很好，但是關鍵在于學生不容易猜想出三邊之間的平方關系，猜想卡殼了，后面的證明就出不來了. 為什么會出現這樣的困難呢？原因有二：一是學生在測量時本身就有誤差；二是從思維角度來看，學生的確很難想到平方關系.

2. 利用方格紙進行探究

提供如圖2、圖3所示的方格紙.

首先，讓學生計算直角三角形三邊的平方分別是多少，只要能計算出三邊的平方，直角三角形三邊之間的平方關系就很容易猜想出來.

這個時候學生會遇到怎樣的困難呢？

因為直角三角形邊長的平方實際上就是每邊上的正方形的面積. 其中正方形1和正方形2的面積可以通過數方格的方法直接數出來，而斜邊上正方形（正方形3）的面積的計算則有一定的困難.

新的問題又出現了，怎么辦呢？方法又有兩個.

（1）“割”，如圖4、圖5所示.

（2）“補”，如圖6、圖7所示.

上述在方格紙上運用內割法或外補法求斜邊上正方形面積的活動蘊含了勾股定理的證明思路，由圖5可得c2=（a-b）2+4ab，由圖7可得（a+b）2=c2+4ab，化簡之后就得到a2+b2=c2. 因此，利用方格紙探究可以幫助學生較順利地猜想出直角三角形三邊的關系，同時水到渠成地獲得定理的證明，使勾股定理的學習一氣呵成.