精彩收尾，二度深入

莊曉健

[摘 要] 作業是學校教育教學行為的一個重要組成部分，它不僅擔負著鞏固、反饋教學效果的職能，還肩負著引領變通、減負提升的效果，如何在教學行為中達成作業的最優化是教師在教學行為中需要不斷實踐和反思的一項教科研行為.

[關鍵詞] 整合；分層；實踐；探索；方法

在新課標背景之下，初中數學教學當中的作業環節成了教師關注的重要問題. 一方面，作業是學生鞏固所學知識必不可少的流程；另一方面，“減負”的要求卻又在限制著課后作業的施行. 這便對課后作業布置的質量提出了更高的要求，即要在不為學生造成過重課業負擔的前提下，實現對知識內容理解的有效重現與深化. 因此，在當前的教學要求之下，想要對課后作業進行切實有效的處理，所應追求的目標不是“多”，而是“精”. 具體說來，可以從適量、梯度、靈活、開放、升華幾個角度進行較為全面的切入.

精煉整合，適量布置課后作業

在當前“減負”的總體教學要求之下，“適量”必須成為課后作業布置當中的首要標準. 然而，作業數量的減少，并不意味著作業質量的下降. 為了能夠讓學生在完成有限數量作業的同時，實現對知識內容的完整回顧，教師就需要對作業內容進行高度精煉的整合，讓課后作業雖然短小精悍，卻可包羅萬象. 這樣的做法，也可以讓學生更加易于并樂于接受課后作業練習.

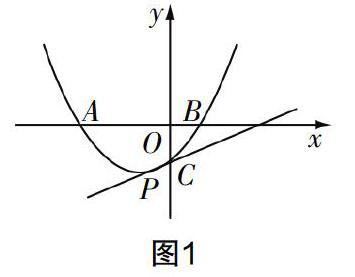
例如，筆者曾經為學生布置了這樣一道習題：如圖1，拋物線y=x2+mx+n與x軸交于點A，B，與y軸交于點C，其頂點為點P，且知點A的橫坐標是-3，點B的橫坐標是1. （1）求m，n的值；（2）求直線CP的解析式；（3）試確定以點A為圓心，以5為直徑的圓與直線CP的位置關系. 雖然只是一道作業題，但其中包含了對直線、拋物線和圓等知識的考查，內容相當豐富. 這樣的課后作業，很好地調動了學生精力的高效率運用.

可以看出，對于知識內容的精練整合，并不是將本次課堂教學內容簡單地羅列后進行壓縮，而是應當將其中的主體重點部分剝離出來，并以清晰的邏輯順序予以串聯與總結，這才是高質量、有效果的整合. 由此，學生得以明確了解所學知識的重點所在，將有限的精力投入到最需要關注的地方，花費最少的時間，完成最優的復習.

分層處理，梯度布置課后作業

在課堂教學過程當中，教師經常會采用分層教學的方式來呈現知識內容. 這種教學思路在課后作業布置環節同樣適用. 隨著每個學生對于所學知識的掌握程度不同，他們對相同的作業內容也會產生不同的感受與認知. 既然學生完成課后作業的時間如此寶貴，就應當讓每一道作業題的完成都能對知識能力進行最大化提升. 因此，教師有必要對作業也進行分層布置，讓不同知識能力的學生都能得到充分鍛煉.

例如，在因式分解內容的課后作業中，筆者將其劃分為三個層次予以呈現：層次一：分解因式3ax2-3ay2，-2xy-x2-y2，x4-81；層次二：利用圖形面積分解因式a2+3ab+2b2，a2+b2+c2+2ab+2ab+2ac；層次三：請從9a2，（x+y）2，1，4b2中任選兩式作差，并將得到的結果因式分解. 另外，請寫出一個三項式，使它能夠先提取公因式，再來運用公式法進行因式分解. 這三個層次的問題難度顯然呈現遞增的趨勢，學生可以根據自己的知識能力進行自由選擇. 這樣的梯度設置，讓每個學生都找到了適合自己的練習入口.

在對單一形式布置作業的效果進行分析時，筆者發現，如果簡單地讓學生去完成相同的課后作業，常常會出現有的學生“吃不飽”，有的學生“吃不了”的現象. 這必將造成前者浪費課后精力，后者畏懼數學學習的不良后果. 當將作業區分難度、梯度進行設計之后，效果明顯好轉了許多. 讓每個學生都能夠在作業完成的過程中各取所需，在能力所及的范圍之內向上伸手夠一夠，才是我們所要追求的有效作業處理.

結合實踐，靈活布置課后作業

數學是一門非常典型的理論性與實踐性兼具的學科，這一點在初中階段的教學當中已經開始較為明顯地體現出來了. 精煉而抽象的理論敘述經常會讓學生感到難以駕馭，而與實際生活建立起聯系之后，學習過程便頓時靈活、具體起來. 由此可見，適時聯系實際的做法，對數學理論教學是具有積極促進作用的. 實踐內容的介入點很多，除了課堂教學之外，還有課后作業.

例如，在學習過函數內容后，筆者請學生在作業中解答這個問題：某公司計劃購入A牌電腦和B牌桌子. 第一次購買了10臺電腦和200張桌子，共花費9萬元；第二次購買了12臺電腦和120張桌子，同樣花費9萬元. 那么電腦和桌子的單價分別是多少？若商場規定：一次購買電腦35臺（含）以上可打九折，一次購買桌子600張（含）以上可打八折. 公司預算27萬元，欲購買不少于35臺電腦和不少于600張桌子，可以制定幾種方案？為了解答這個問題，學生很自然地運用到了剛剛學習過的方程知識，并從中找到了不等式知識在實際生活中的應用方向.

課后作業很大一個職能就是為學生搭建一個學以致用的平臺. 因此，在課后作業當中融入實踐性質的內容，與教師想要借助作業達到的教學效果是相得益彰的. 如果說，課堂教學當中的實踐內容告訴了學生“數學在哪里”，那么課后作業當中的實踐性內容的加入則帶領學生明白了“數學怎么用”. 兼具理論與實踐的靈活作業布置，不僅能夠讓學生從中找到學習的樂趣，更可以在實踐的過程中更進一步理解知識.

大膽探索，開放布置課后作業

為了達到二度深入知識學習的目標，課后作業的內容應當是豐富的. 筆者在教學實踐當中，總是會讓每一次課后作業由兩部分內容組成：基礎內容與開放內容. 基礎內容旨在從概念、定理等角度入手，夯實基礎，重溫所學，而開放內容則是為了提升能力水平. 很多教師總是認為初中學生的數學基礎有限，不敢將開放性問題交給他們，實則不然. 過于常規的基礎性練習往往會禁錮住學生的靈活思維，這是對數學能力提升極為不利的. 課后作業需要開放性內容，數學學習需要探究的過程.

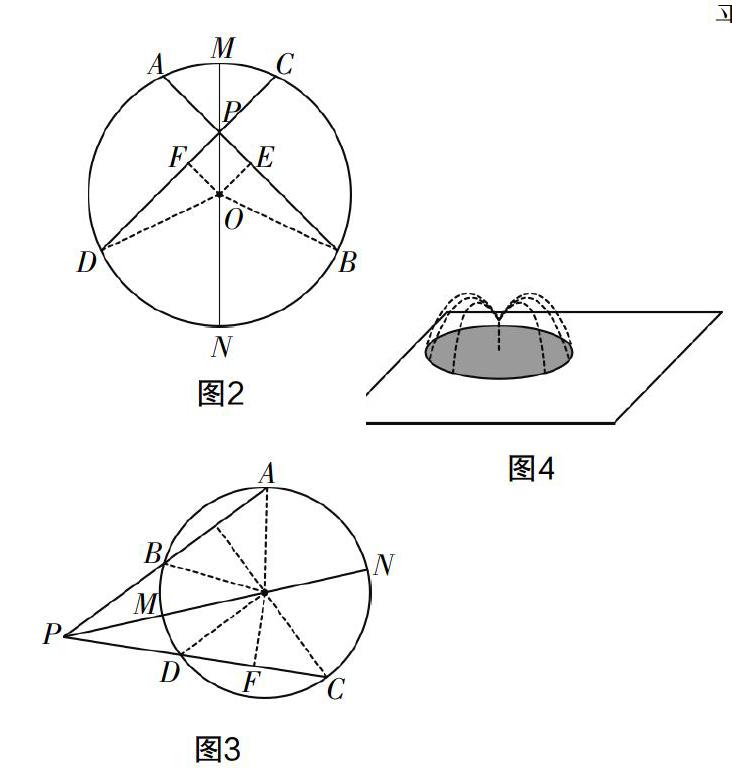
例如，在學習過圓的內容之后，筆者在作業當中為學生布置了這樣一道習題：如圖2所示，MN是⊙O的直徑，弦AB和CD相交于MN上的點P，且∠MPA=∠MPC. （1）根據上述條件，請試著判斷AB和CD的大小關系，并說明理由. （2）如圖3所示，若交點P在⊙O之外，那么，上面的結論是否依然成立？如果成立，加以證明；如果不成立，說明理由. 這個問題的提出是相當靈活的，給學生留下了很大的自由探究空間. 通過這一題目的練習，學生總結出，在處理探究問題時，應當先進行合理猜想，再向著猜想的方向進行證明. 具體至這道題，大家通過圖像判斷AB=CD，也就明確了論證方向. 在這個過程中，學生對于圓的認知也更加深入了.

在初中階段的各類數學測試當中，已經開始越來越多地出現探究性問題的身影了，足見其對于初中數學教學的價值. 的確，對于探究性問題的解答，能夠大大開闊學生的思維視野. 因此，無論是從提高考試成績還是從深化學習效果的角度來看，在課后作業環節再現數學探究都是勢在必行的. 起初，一些學生會感到一定程度的解答困難，但只要在不斷堅持中找到思維出口，收獲的效果將是十分喜人的.

突顯方法，升華布置課后作業

如果僅從一個個知識點的角度出發去學習知識，各個擊破，對于數學的掌握雖然全面，卻難免陷入過于零散的困境. 想要獲得優質高效的學習效果，就要學會從宏觀上看待知識，從具體的數學內容當中提煉出思想方法，以之串聯起所有知識點，提綱挈領，事半功倍. 這里所說的思想方法，并不是依靠教師的語言描述就能夠讓學生切實掌握的，它需要學生在親自解答數學問題時去感受和發現. 當然，教師也要在這時為發現方法創造機會，特別是在課后作業的布置當中對思想方法予以突顯.

例如，有一道作業題曾經讓不少學生犯了難：某公園想要在邊長為16 m的正方形草坪上安裝噴水龍頭，需要讓整片草坪都能噴灑到水. 若每個噴水龍頭能夠噴灑到半徑為6 m的圓面（如圖4），那么至少需要在草坪中安裝幾個龍頭？如果僅靠題目當中給出的圖進行判斷是很難的. 這時，如果能夠將噴水的效果以平面圖來表示，并省略噴水過程，直接以圓的模型進行思考，實際問題便一下子成了純粹的數學問題. 這就是典型的數形結合過程，也是初中數學問題解答中最為常用的思想方法之一.

為了讓學生能夠在進行練習的過程中自然而然地發現典型思想方法之所在，需要教師在設計課后作業時特別注意. 筆者在作業當中常常會運用能夠突顯數學方法的題目，強化學生的心理感知. 經過課后作業當中的巧妙設計，學生在解題過程中十分明顯地感受到了典型方法對問題解答的作用. 對學生存在解答困難的問題，教師在講解時也得以開門見山地擺出思想方法，著重加深大家對之的印象，進而站在一個新的高度審視數學，認知數學，掌握數學.

課后作業是數學知識學習的階段性小結. 作為課堂教學的收尾，課后作業所承擔的任務是非常重大的. 首先，它應當能夠比較全面地涵蓋本次課堂教學的知識內容，起到幫助學習回顧和鞏固所學的作用. 同時，還應當將重點內容予以突出，將思想方法抽象提煉，讓學生在完成作業的同時深化知識理解. 正因如此，課后作業之于數學教學才如此意義重大，尤其是對數學能力基礎尚未完全建立起來的初中階段學生來講，課后作業的輔助功能便更顯重要了. 希望廣大教師能夠將更多教學智慧投入到課后作業的設計與實施當中，給課堂教學以精彩收尾，給知識體悟以二度深入.