關于初中數學習題教學的實踐探究

朱悅

【摘要】 在初中數學教學中，習題教學是極為重要的構成部分，對培養學生數學思維方式、解題技巧、應用能力等起到極為關鍵的作用. 本文在闡述初中數學習題教學重要地位及作用的基礎上，結合影響其教學效果的主要因素，探究了加強初中習題教學質量的有效實踐策略.

【關鍵詞】 初中數學；習題教學；實踐探究

引 言

習題教學主要指在課堂教學中，教師為深化學生對所學知識的理解，圍繞數學教材習題所開展的一系列教學活動. 在初中課程教學中，數學習題教學是極為重要的一部分，貫穿于數學教學的全過程，對落實素質教學、拓寬學生數學思維、增強學生應用能力起到不可替代的作用. 因此，教師要提高數學教學質量，必須合理組織習題教學實踐，充分發揮出數學習題作用對學生的促進作用.

1. 習題在初中數學教學中的地位及作用

數學習題是對教材內容及知識點的總結、提煉以及融會貫通，具備較強的綜合性、應用性、啟發性以及創新性. 教師通過數學習題教學，將習題解析中應用到的數學思想、數學知識、解題技能等靈活地展示給學生，以幫助初中階段學生更好地領悟與鞏固所學知識，并掌握相關知識應用能力及解題技巧.

2. 影響初中數學習題教學的主要因素

2.1 數學本身特點

初中數學相比于語文、政治等其他課程，具備較為明顯的差異性特征，對學生的邏輯思維能力、領悟力以及實踐應用能力有著較高要求. 總體而言，數學具有抽象性、準確性以及廣泛性三大主要特征. 數學的抽象性主要表現在其概念及驗證方法上，其他物理化學家在論斷證明方面，往往可借助真實的試驗得到結果，而數學家則只能以推理或數據計算的形式進行. 同時，數學定義定理要求必須精準，推理過程嚴謹及邏輯脈絡清晰，而最終獲得的數學結論具備無可爭議性.

2.2 初中生的認知特點

初中生作為初中數學教學的主體，其認知特點直接影響到習題教學的效果. 在初中階段的學生，普遍處于青少年時期，生理與心理發育尚未成熟，在課堂教學中往往表現出較強的自我意識，且注意力難以集中，認知能力還有待提升. 在邏輯思維方面，初中生整體表現出較為顯著的敏銳性、不成熟性以及可訓練性. 因此，教師在習題教學中，應遵循這一階段學生的認知特征，基于其認知水平開展各項習題教學活動，靈活運用多種教學方法與技巧，調動學生的學習積極性，并為學生留有充足的思考空間，以更好地鍛煉其數學思維能力，促進學生的全面發展.

2.3 教師教學水平

教師作為初中數學習題教學活動的組織者、引導者，其教學水平的高低也會對習題教學質量造成極大的影響. 教師的教學水平包括教學經驗、教學觀念、教學方法等. 教學經驗豐富的教師往往能更好地把握教學全局，針對學生心理及學習狀態，善于用巧妙、生動的語言、靈活的習題教學內容設計，高效的教學實踐活動組織，來達到預期的教學效果. 其中，教師的語言表述能力是極為重要的，由于數學課程本身涉及大量的理論知識、數據分析等，一旦教師以按部就班的形式進行講解，極易讓學生感到枯燥乏味，進而逐漸喪失對數學的學習探索欲望. 因此，初中數學教師在習題教學中，必須考慮到自身因素，不斷提升自身教學水平，學會運用語言藝術，以生動、幽默又富有邏輯性的語言來引導學生投入到學習中，共同體驗數學習題的解答過程.

3. 提高初中數學習題教學水平的實踐探究

3.1 創設情境，探究學習

長期以來，初中數學教師在習題教學中，通常都是照本宣科、就題論題，過于強調對學生課本知識的掌握程度及解題的規范性，而忽視了學生的個性差異，學生在習題教學中難以集中注意力，學習效果不佳. 為此，教師需要改變這種傳統的習題教學模式，結合初中生的整體認知特征及個性差異，利用多媒體技術，合理創設情境，將數學習題融入到多樣化的問題情境中去，調動學生的探知欲望，通過帶有啟發性的問題情境設置，來引導學生主動參與教學，開拓思維、積極思考問題隱藏的深意. 同時，增強問題情境的趣味性，激發學生對數學習題的濃厚興趣.

例如：在一定范圍的池塘內，先捕捉50條魚作出標注，再放回池塘內，待有標注的魚完全混入到魚群中去后，開展第二次捕撈行為，所捕魚數量為200條，其中，帶有標注的魚為10條，以此推測池塘中大概有多少條魚？此題主要是考查學生對樣本估計總體的知識掌握程度，教師可利用多媒體軟件，演示池塘內捕魚推測過程，學生在觀察實物圖的基礎上，能思維更活躍地進行習題解答及演算.

3.2 挖掘隱藏于習題中的數學思想方法

數學思想方法主要指在習題解析過程中，應用到的多種思維方式、解題策略、解題手段、技巧及途徑等. 教師在習題教學中，應注重對其題目中隱藏數學思想方法的挖掘，根據初中生的認知特征及知識掌握程度，在科學數學思想的指導下，嘗試以多種方法與途徑向學生演示習題的解析過程，或鼓勵學生進行解題創新，嘗試采用新的方法來解答題目，以增強學生的思維創新能力及實踐應用能力.

例如，在題目“已知二次函數的圖像頂點為（1，-8），并經過點（3，0），求此二次函數解析式. ”教師便可引導學生采取兩種解題方法完成題目解答.

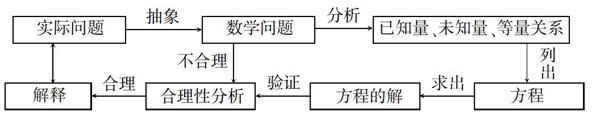
解法二：根據題目已給條件，設定解析式為y = a（x - 1）2 - 8，然后再將點（3，0）代入其解析式內，得出0 = a（3 - 1）2 - 8，a = 2，進而得出y = 2（x - 1）2 - 8，y = 2x2 - 4x - 6. 在這一題目解析中，方程思想圍繞已知與未知的對立統一關系，既可利用點坐標布列方程組，也可利用頂點式求解.

3.3 構建模型，培養學生應用意識

在初中數學習題教學中，教師需考慮到數學本身的抽象性，針對習題構建相應的模型，將解題思路及解題過程具體化，以便于學生更好地分析問題、理清思路，在習題解答中逐步構建完整的知識體系.

例如，題目：某服裝店按商品成本價，在提高40%后，又以8折優惠銷售，使得每件商品仍可獲利15元，求商品的成本價？對于這道習題，教師可構建一元一次方程模型：