數學教學中開放題的應用
黃敏芝(武夷山旅游職業中專學校,福建 武夷山 354300)
?
數學教學中開放題的應用
黃敏芝
(武夷山旅游職業中專學校,福建 武夷山354300)
摘要:隨著數學素質教育不斷深入,開放性問題教學的重要性已越來越被廣大數學教師所認識。如何得用現有教材開展開放性問題的教學?是本文所要闡述的主要內容。
關鍵詞:創新;思維發展;認知需求
開放題教學是一種新的數學教學模式,教師必須認識開放題材的作用,根據實際情況利用現有傳統題目,開展開放性問題的教學,以適應數學教學的要求。
一、數學開放題的作用
要開展開放性問題的教學,首先要明確開放題的作用:數學開放題有助于增加鼓勵和表揚學生機會。有助于開闊學生的視野;學生積極參加學習,發言次數增多,不同層次的學生能做出相應的某種意義的回答;學生增加發現問題和為人所認可的成就感;并可將所學知識綜合利用。具體表現在以下幾方面:
1.有利于培養學生的創新意識。
由于開放題的答案不唯一,給學生提供了較多提出自己獨特的機會,培養學生的創新意識。
2.有利于培養學生良好的思維品質。
由于開放題要求學生尋求條件,結論,尋求不同解法。充分培養學生逆向思維,發散性思維,同時有助于培養學生思維的深刻性,廣闊性,創造性,嚴密性,批判性,進而培養的思維品質。
3.有利于提高學生的主體地位,增強學生學習積極性。
由于開放題有層次性,有利于激發學生的好奇心和求知欲,為學生主動學習創造條件,使用不同層次的學生都能發揮主觀能動性,進而達到學有所獲的效果。
二、教學實踐中開放題的幾種開展方法
1.弱化成題的條件,使其結論多樣化。
例1.如圖1ΔABC是一個鈉架,AB=AC,AD是連結A與BC中點D的支架。求證:AD⊥BC(《幾何》課本第二冊第38頁)

改編為:如圖1,△ABC是一個房屋的人字梁,其中AB=AC為了使人字兩梁更加穩固,房主要求木工頂點,A和橫梁BC之間,加一根柱子AD,你能幫助木工確定D點在BC何處,才能使AD⊥BC嗎?
寫出方案,,并說明理由.
由于減少D是BC中點條件,便讓學生有進行發散性思維的空間.有。有的學生憑直覺大膽猜想D為BC中點;也有學生會根據生活經驗,用懸掛重物的方法尋求D點;還有學生想先拉根細線,再用三角板;還有學生說將一矩形長板塊靠在A處并使用權矩形較矩邊話在橫梁上來確定D點。
學生依靠傳統命題解題思路,逆向尋找被隱去的條件,喚起他們對問題解決的需要,并且能使學生產生對問題解決思考途徑的一種反思。從而加絕對概念本質的理解。
2.隱去成題的結論,使其指向多樣性。例2,如圖2 ,AB是⊙ο的直徑,⊙ο過BC的中點D,DE⊥AC,求證:DE是⊙ο的切線。(《幾何》第二冊第15頁)改編為:如圖2,AB是⊙ο的直徑,⊙ο過BC中點D,DE⊥AE,垂足為E。

⑴由這些條件,你能推出哪些正確的結論?(要求:不用標注其它字母,如有連輔助線,則應不在結論中出現)
⑵若∠BAC為直角,其它條件不變,除上述結論外,你還能推出哪些新的正確結論?并簡要說明理由。
由于隱去原題中結論,使得結論待定化和多樣化。這樣讓學生能充分利用所學有關平行、相似及圓的知識來發現結論,有些甚至會很有新意。
有些問題的答案不確定,解答具有多樣性,這決定了它能滿足多種層次學生認知需求,有利于學生解答過程中重建認識結構。同時由于綜合知識的容量加大,教師可有針對性地把學生分層次地加以引導提高。激發學生學習的好奇心,調動全體學生參加解答過程。
三、將原題特殊化、一般化
例3:求證:等腰三角形底邊上任一定點,與兩腰的距離和等于腰上的高。
改編為:如圖3、在等腰三梯形ABCD中,已知AD∥BC,AB=DC,點P為BC上一點,PE⊥AB,PF⊥CD,BG⊥CD,垂足分別為E、F、G。求證:BE+CF=BG
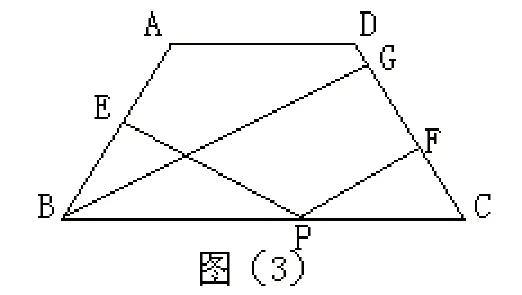
將原題特殊化,即將等腰三解形變化等腰梯形,其條件,證法相似,便于讓學生將知識延伸,達到舉一反三的效果。
數學問題的結論往往是在一定條件基礎上,由某些特殊條件建構或衍生的特定結果。以現有結論出發,進行聯想,探索成立的特殊件,引導學生在求解過程中引出新問題,并將問題加以推廣,找出更一般、更概括的結論。
四、開放題應側重解決問題的思路和策略
學習不應是簡單地感知,被動地接受,而需要學生自身積極能動地構造,通過建構,實現主體思維的拓展。通過開放性教學,學生主體精神能更好得以體現,因此應側重解決問題的思路和策略而不是問題答案,則應注意以下幾點。
1.斥其他問題的作用。如培養學生運算能力,使學生會根據法則,公式等正確運算,根據問題條件設計合理,簡捷運算途徑還得借助傳統教學。
2.教師要做好示范。在開放性問題教學中,教師應自覺形成開放的意識,將教學語言演繹得豐富多彩。并處處創設問題的情境,讓學生能過動手,動腦,發現規律,找分關系,體驗創造性勞動的樂趣,老師在問答過程中起鼓勵,指導作用。
3.要注意學生的認識層次,要滿足不同學生的需求,對不同思維發展水平學生,應從實際出發,同時,將問題接不同梯度展開,給每個學生有發現的余地,有的放矢地給出一些啟發和幫助,從而達到共同提高的目的。必須避免將開放題變成難題,怪題,讓學生望而生畏。
綜合上述,開放性問題的教學核心是培養學生的創新意思和實踐能力。讓學生懂得用現代看法解決現代問題僅僅是學習的開始,更重要的是發現新問題,提出新問題,解決新問題,這才是開展開放性問題教學的一種目的所在。
參考文獻:
[1]聞黎明“平面幾何題改編為開放題的一些做法”《數學教學》。
[2]劉達“由開放性問題設計而產生的開放性問題”《數學教學》。
中圖分類號:G633.6
文獻標識碼:A
文章編號:1671-864X(2016)06-0262-01

