提高學生數學解題能力的幾條途徑

黃耀平

[摘 要] 教師在教學中，能否提高學生的解題能力，直接關系到學生學習數學的成功與否. 本文結合教學實踐與思考，闡述提高數學解題能力的4種有效途徑：理解概念定理，總結規律方法，探究知識的延伸，關注非智力因素的應用等. 這些方法在教學實踐中對于提高學生的解題能力起到了一定的幫助.

[關鍵詞] 數學；解題能力；途徑

數學學習實際上是一種能力的學習，只有學生的解題能力提高了，成績才會出來，才算把數學學到了手. 那如何才能提高學生的數學解題能力呢？

從基礎入手，深入理解概念定理

數學知識的學習是一個不斷扎實累積的過程，對于基礎內容必須尤為關注. 也只有將知識基礎夯實了，才有可能以之為工具去解答具體的數學問題. 也只有從根本上將知識內容把握住了，學生在面對復雜問題時才能有所依據，游刃有余. 具體來講，高中數學的基礎部分主要指的就是概念與定理，它們就像是構成知識大廈的一磚一瓦，對于之后的問題解答起著至關重要的作用.

例如，在對函數知識進行教學時，對其概念的理解是第一步. 然而，很多學生卻沒有產生足夠重視. 于是，筆者在課堂上提出了這樣一個問題：若一系列函數的解析式相同，值域相同，但其定義域不同，則稱這些函數為“同族函數”. 那么，函數解析式為f（x）=x2，值域為{1，4}的“同族函數”共有多少個？這個問題的提出，將學生的注意力馬上轉移到了對解析式、定義域、值域等基本概念的關注上. 這不僅引起了大家對于基本知識內容的重視，還讓學生很自然地回到了知識初始，重新對相關概念進行鞏固理解，效果很好.

很多學生在剛剛接觸一個新的知識內容時，往往對于概念定理等基本知識內容的重視程度不夠，認為這些都是程式化的東西，總是蜻蜓點水一帶而過. 如此薄弱的知識基礎將會為具體問題的解答帶來極為嚴重的阻礙. 當已經進入到問題解答階段再發現這些基礎問題時，就有些為時已晚了，彌補修復的精力也會大大增加. 因此，在第一時間夯實知識基礎，是培養解題能力的第一步.

從過程入手，細致總結規律方法

當然，解題的主體過程是解題能力得以表現的核心環節，自然也是培養學生解題能力的主要入手點. 在這之中，教師要做的是將解題的過程放慢，并不斷細化，加強學生的過程性體驗，從中總結出對應不同特點數學問題的規律方法，由此提高效率，強化能力. 相比于具體知識內容的學習來講，這個總結方法的工作顯然難度加大了. 教師應當對此加入適當的干預和引導，輔助規律方法的發現順利進行.

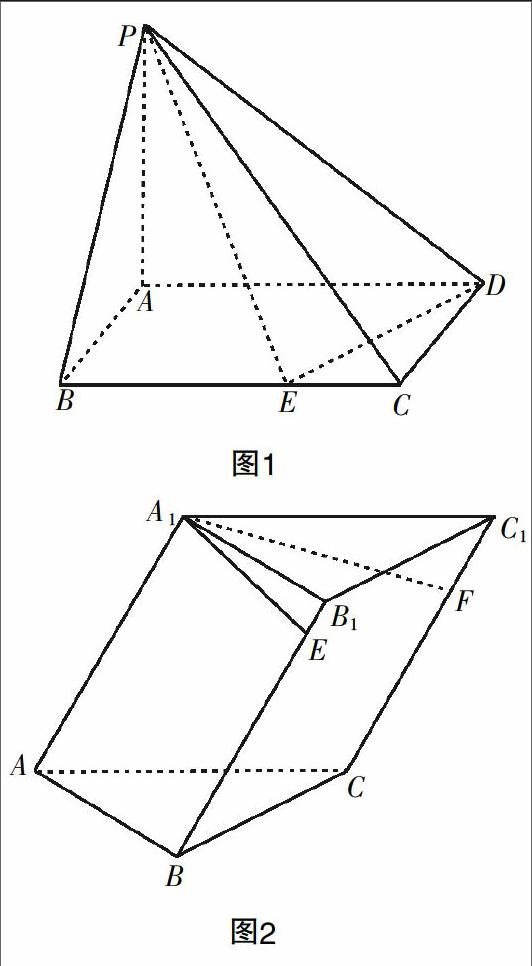
例如，在對直線與平面垂直的性質的內容進行教學時，學生遇到了這樣一個問題：如圖1所示，在四棱錐P-ABCD中，PA⊥底面ABCD，底面四邊形ABCD是矩形，且AD=3AB，點E是底面的邊BC上的動點，設BE ∶ BC=λ（0<λ<1），則滿足PE⊥DE的λ值有多少個？這個問題的提法有些開放性的特點，讓不少學生有些犯難. 在對之進行講解時，筆者不僅將解題過程予以體現，更抓住了其中的思維關鍵，即判定點E在以AD為直徑的圓上，作為本類題目解答的核心加以闡釋. 這不僅讓學生明白了三垂線定理以及直線與圓的位置關系內容的運用方向是什么，更明確了類似問題的思維目標. 先明確了分析目標，再由已知條件推導思路，顯然會高效許多，這就是學生在練習當中所要感悟的規律與方法.

掌握規律與方法對于高中數學解題過程來講，是一條頗具價值的捷徑，更是解題能力提升的關鍵. 尋找規律方法的同時，實際上就是一個在對數學問題總結特點、進行分類的過程. 找到方法之后，學生自然已經對相關問題完成了具體且深入的分析，對于當前方法的印象也必然更加明確深入. 在這樣的思路引導下，學生的解題能力也隨之實現了明顯強化.

從思維入手，靈活探究延伸知識

如果說從方法入手，是具化角度的能力關注，那么，如果想要繼續實現更高層次的解題能力的提升，就要站在思維的高度設計教學活動了. 在對教學活動與數學問題進行設計時，教師要抬高視野，提前想到這會引發學生的何種思維方式與活動，且這樣的思維效果是不是本次課堂教學所預期的. 從這個角度出發開展教學，顯然能夠更加準確地指向學生的解題能力，教學效果自然也就更為理想.

例如，在對空間角和距離的內容進行教學時，筆者為學生提出了這樣一個問題：如圖2所示，已知三棱柱ABC-A1B1C1的底面是邊長為2的正三角形，側棱AA1與AB，AC均成45°角，且A1E⊥B1B于點E，A1F⊥CC1于點F. （1）求點A到平面B1BCC1的距離；（2）當AA1多長時，點A1到平面ABC與平面B1BCC1的距離相等. 在這個問題中，第一問是比較基本的問題，而到了第二問就顯現出靈活探究的特征了. 對此，筆者將學生進行分組，由大家相互討論，自由尋找問題解答的突破點. 在這樣的訓練之下，學生漸漸開始敢于打開思維、表達思想了，解題能力也在這個過程中明顯進步了.

不難發現，從思維角度進行的教學設計更易于瞄準知識延伸的部分做文章. 特別是在高中階段的知識教學當中，教師不能再僅僅滿足于基本的知識內容，而是要將之拓展至靈活思維的領域，對既有知識進行深入探究，不斷拓展學習外延，將學生的學習收獲實現由知識到能力的增強. 通過教學實踐中的相關活動設計，學生很順利地走到了自主探究的路徑之中，思維能力也較從前提升了許多.

從環境入手，關注智商之外的因素

前文所述的因素都是從數學知識學習本身的角度提出的，我們可以將之統稱為智力因素，即與學生對于知識內容的主觀反映有關的影響因素. 除此之外，還有一個重要的影響來源是不容忽視的，那就是以教學環境為代表的智力外因素. 通過與很多高中數學教師進行交流探討，筆者發現，智力之外的影響因素總是沒有被教師納入教學設計的考慮，其對于數學思維培養所具有的作用自然也就鮮少得到彰顯了. 這是高中數學教學之中的一個重大誤區，需要廣大教師及時意識到并加以必要的重視.

例如，在對解析幾何中的雙曲線內容進行教學時，筆者將基本內容呈現完畢后，并沒有繼續以理論性的語言進行知識運用方面的教授，而是為學生設置了一個以實際應用為背景的問題：某工程要將直線公路l一側的土石，通過公路上的兩個道口A和B，沿著道路AP，BP運往公路另一側的P處，PA長為100米，PB長為150米，∠APB的度數為60°. 試說明：怎樣運輸土石能夠最省工時？這種實際操作氛圍下的問題解決，很容易引起學生的關注熱情. 在積極主動的問題分析當中，大家意識到了雙曲線知識的適用. 這樣的實踐環境，不僅提升了大家的學習熱情，更為學生打開了學以致用的思維通道. 養成了勤于聯系實際的思維習慣后，對于解題能力的促進將是十分顯著的.

在高中階段知識教學的嚴峻壓力之下，課堂學習環境的構建已經很少能引起教師們的重視了，然而它對于學生思維能力的影響卻是很大的，整體學習氛圍對于學生思維的干預是潛移默化的. 如果教師能夠將課堂教學環境創設好，把控好，很多思維訓練的要求無須直截了當地提出，而是可以將相關措施融入環境氛圍當中. 以非智力因素來激發學生的求知熱情，并逐步探尋應有的思維模式，其教學效果往往更加事半功倍.

通過對解題過程進行分析不難發現，不同的解題環節與不同的問題內容形式對于解題能力的要求都是不盡相同的. 因此，教師在以解題能力為前提進行教學設計時，需要不斷開闊視野，盡可能地將能力培養的覆蓋面擴展，借助多樣化的問題體驗來感受不同的解題方式，并從影響解題能力形成的多種因素綜合入手，力爭在最少的精力消耗下實現最優的解題能力提升. 本文當中所討論的是筆者在教學實踐中認為比較關鍵的幾個切入角度，希望能夠為廣大教師提供啟發，發掘出更多更好的解題能力培養路徑，為富有實效的高中數學教學增光添彩.