小學數學猜想教學的策略研究

馮喆

（浙江省臺州市仙居縣實驗小學，臺州318000）

【摘 要】猜想是一個多向思維的心理過程，對學生數學能力的培養有決定性的作用。猜想教學的應用應該選取恰當的機會。同時運用猜想要注意合理有效，要與驗證相結合，教師還要對學生的猜想進行恰當的鼓勵引導，從而使學生經由猜想的過程積極主動地參與到知識的建構中。

【關鍵詞】小學數學；問題創設；猜想教學；猜想驗證

一、深挖教材，拓寬思路

新的人教版小學數學課本中蘊含了許多猜想的素材。教師應該深入挖掘教材資源內容，為學生的猜想提供更多的機會。

（一）巧用新教材中的“提示語”，引導猜想

新教材在例題以及配套練習的旁邊經常會出現一些提示語“還可以怎么想？”“你發現了什么？”學生閱讀課本時，教師可以利用這些提示語引導學生進行猜想，使學生在觀察、猜想中掌握規律。

例如人教版小學數學六年級下冊《比例的基本性質》

猜想教學片段：猜數

老師這里有一個比例“12：□=□：2”，不過它的兩個內項看不清了，猜一猜，這兩個內項可能是哪兩個數？（如1和24，2和12，……）

追問：正確嗎？為什么？（求比值判斷）還有不同答案嗎？

只能是整數的例子嗎？這樣的例子舉得完嗎？

仔細觀察這組等式，你有什么發現？（兩個外項的積等于兩個內項的積；兩個內項的位置可以交換……）

（二）巧用新教材中的“空白點”，啟迪猜想

新教材在內容呈現中有許多的留白，一些定義、規律并不明明白白地呈現出來，而是以“像……這樣”舉例的形式出現。在這種情況下，教師應該充分利用這一空白，引導學生進行有效的猜想。

（三）巧用教材中的“想一想”，啟發猜想

新教材中的小精靈常常會帶來許多問題，在這些問題出現時，教師要善于激發學生的猜想，鼓勵學生從不同角度進行猜想。

例如人教版小學數學三年級上冊《口算乘法》

猜想教學片段：猜想20×3=？

“你是怎么想的？”

20×3=60

2個十×3=6個十

同桌互相說一說，你是怎么想的？

2×3= 6×5= 2×8=

20×3= 60×5= 20×8=

200×3= 600×5= 200×8=

2000×3= 6000×5= 2000×8=

只計算第一列，猜測規律，并運用規律完成后2列。

（四）有效改編教材的呈現形式與順序，擴大學生猜測的空間

一些學生自己易于發現的數學理論，教師可以有目的地改變它們的呈現順序，促使學生通過自己的猜想來驗證它。

例如人教版小學數學一年級下冊《找規律》

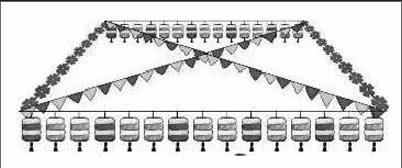
猜想教學片段：出示燈籠主題圖

仔細觀察燈籠，你發現什么規律？和同桌說一說。

按這樣的規律排下去，猜一猜下一個會怎樣？（驗證猜想）

猜一猜往后第2個會和誰一樣呢？第3、第4呢？規律？

為什么剛好是3個重復呢？和什么有關？

揭示規律并驗證。

二、創設問題，激發欲望

合理的數學猜想憑借的是直覺思維。在知識的新授過程中，教師應該提供有聯系的教學材料，創設具有挑戰性的問題情境，組織學生觀察、比較、合作、探究，引導學生有效地猜想。

（一）設置陷阱，激發求知欲

教師可以在數學課堂教學中針對教學內容經常創設一些讓學生猜想的情境，這樣的“猜測”情境，強有力地激發了學生的求知欲，有效突出教學重難點。

例如：人教版小學數學六年級下冊《圓錐的體積》

猜想教學片段：

在教學圓錐的體積計算時刻意讓學生猜想：將一塊長為50厘米，寬為40厘米，高為30厘米的長方形木料加工成一個圓錐，怎樣加工能使圓錐體積最大？要使圓錐的體積最大，要優先考慮什么條件？

學生通過分析、思考做出的猜想充分暴露了學生學習中的疑難點和不當的思維定勢，猜想的思維過程與結果，能有效促進學生的創新思維能力的發展。

（二）利用遷移，引發猜想

1. 抓住相似點，引發類比猜想

啟發學生探究新舊知識之間的相似之處，通過類比猜想獲得知識。根據舊知中的特點猜想新知中可能也存在相同的特點，進而解決新知中的問題。

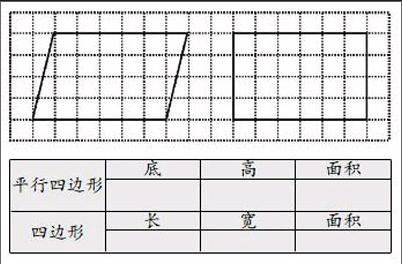
例如人教版小學數學五年級上冊《平行四邊形的面積》

猜想教學片段：

出示一個長方形的學具，復習長方形的面積計算方法，然后拉動長方形的兩邊變成平行四邊形。現在你會求它的面積嗎？

不滿一格時怎么數呢？還有其他更簡便的方法嗎？

你能不能把平行四邊形變成學過的圖形，再求面積呢？

猜想：平行四邊形轉化成長方形后，兩者之間有什么聯系呢？

2. 抓住內在聯系，引發推理猜想

要善于發現這樣的聯系，切不可每節課都從“0”開始，要巧妙利用聯系點，運用推理猜想舉一反三，獲得事半功倍的效果。

例如人教版小學數學六年級上冊《比的基本性質》

猜想教學片段：

師：我們先來整理一下除法、分數、比這三個相關聯的知識點。

師：商不變性質、分數的基本性質，那么你有什么猜想？

根據除法、分數、比之間的對比，再到商不變性質，分數的基本性質，然后引發猜想。學生能夠馬上得出結論，比的基本性質的內容與重難點也可以在對比中一目了然。

三、注重猜想驗證，體會數學的嚴謹性

教師在組織學生進行第一次的“猜想—驗證”之后，更要繼續深入引導學生進行“二次猜想—二次驗證”，通過不斷深入猜想，引申結論，完善認識。正是在這樣的循環過程中，學生變成了發明家、科學家，數學學習變成了科學發現的過程，學生對數學知識的認識也經歷了“模糊—清晰—混淆—掌握”的螺旋上升的過程。

例如人教版小學數學三年級下冊《長方形和正方形面積計算》

猜想教學片段：

擺一擺將6個面積1平方厘米的小正方形拼成長方形，你有多少種不同的擺法？

長 寬 長方形面積

6厘米 1厘米 6平方厘米

3厘米 2厘米 6平方厘米

觀察這2種擺法，猜想長方形長、寬、面積之間有什么聯系？

如果是12個小正方形還會符合這個結論嗎？你還能舉出其他的例子驗證嗎？

仔細觀察格子圖，你還有什么方法驗證結論呢？

學生猜測出長方形面積計算公式后，及時引導學生去驗證“猜想”，使學生對于公式進行更深入的探究。

四、猜想教學應注意的幾個方面

在運用猜想教學時教師一定要注重探索、研究，不可盲目猜想。具體應該注意以下三點。

1. 給予每位孩子猜想的機會與空間。為孩子創設寬松環境，激勵學生勇于猜測。允許孩子有不同的猜想，讓孩子在輕松的氛圍中敢于猜想。

2. 積極引導學生猜想，讓學生學會猜想的方法。讓學生清楚認識到猜想是建立在已有的知識和經驗上，通過觀察、比較、歸納、類比等方法獲得的，并不是隨意猜測。

3. 要加強猜后檢驗，不斷提高猜測水平。檢驗是猜想變成結論的必經之路，每次猜想之后就要通過計算、舉例、實驗、操作等方式進行反思，最終得出正確的結論，獲得知識。

參考文獻

[1]孔企平.小學兒童如何學數學[M].上海：華東師范大學出版社，2001.

[2]季蘋.新課程與學校發展[M].北京：教育科學出版社，2002.