從提高學生運算能力的角度談數學核心素養的培養

[摘 要] 數學核心素養是數學學習者在學習數學或學習數學某一個領域所應達成的綜合性能力. 與高中數學相關的核心素養主要包括：學會學習、應用能力、創新意識、抽象概括、推理能力、數學建模、運算能力、幾何直觀、數據分析，其中前三項為通識素養，后六項為數學素養. 數學核心素養是數學教與學過程中應當特別關注的基本素養. “能推理、會運算”是從數學的學習中養成的基本素質. 運算能力的培養與學生的素養相輔相成.

[關鍵詞] 學生素養；數學素養；數學核心素養；運算能力

隨著基礎教育課程改革的不斷深入，學生素養的培養越來越為人們所關注. 就數學學科而言，學生數學素養的提高，特別是數學核心素養的培養，已經引起許多數學教師的思考和探索. 核心素養是指學生借助學校教育所形成的解決問題的素養與能力. 數學核心素養是數學學習者在學習數學或學習數學某一個領域所應達成的綜合性能力. 與高中數學相關的核心素養主要包括：學會學習、應用能力、創新意識、抽象概括、推理能力、數學建模、運算能力、幾何直觀、數據分析，其中前三項為通識素養，后六項為數學素養. 數學核心素養是數學教與學過程中應當特別關注的基本素養.

近年來，各地的高考試題一直關注對數學核心素養中的運算能力的考查，要求考生在理解、應用、實施運算過程中，分析運算條件，探究運算方向，選擇運算方法，設計運算程序（考查算法算理）. 運算能力的培養與學生的素養相輔相成，主體上無法靠簡單的訓練形成，在高三復習過程中需要重視以下幾個操作層面.

[?] 著眼于扎實的數學基礎知識和基本技能

落實基本概念、公式、法則的理解是思維和運算的“基元”. 在數學教學中，讓學生牢固掌握運算所需要的概念、公式、法則是運算的前提.

例1：已知數列{an}是等比數列，其前n項和為Sn，若Sn+1，Sn，Sn+2成等差數列，則公比q的值為______.

在列出等式2Sn=Sn+1+Sn+2后，利用數列前n項和的定義有：2Sn=Sn+an+1+Sn+an+1+an+2，即0=an+1+an+1+an+2，所以q=-2. 方法簡明，體現了對定義的理解.在理解概念的基礎上自覺用來進行運算，說明學生在這方面具備了一定的數學素養. 個別學生往往會按照思維慣性利用等比數列前n項和的公式來求解，過程相對煩瑣，而且容易忽視q=1的情形，說明運算方面的素養仍需提高.

除了熟記和活用概念、公式外，對于一些典型問題的結論和方法也要熟化，更要弄清楚這些典型問題的結構和背景，使其結論能夠生發，方法能夠遷移，成為運算的“助推器”.

例2：在平面直角坐標系xOy中，F1，F2分別為橢圓+=1（a>b>0）的左、右焦點，B，C分別為橢圓的上、下頂點，直線BF2與橢圓的另一個交點為D. 若tan∠F1BO=，則直線CD的斜率為______.

本題由tan∠F1BO=可得直線BD的斜率，利用結論“在橢圓+=1（a>b>0）中，若MN是過中心的一條弦，P是橢圓上異于M，N的一點，則有kPM·kPN= -”，可迅速求得直線CD的斜率.

在復習過程中學生可在教師的帶領下，或自主將知識歸類整理，把知識對應的問題及解法進行梳理、歸納，使得解法模式化，適度重復使用，形成技能，便于遇到問題時能在短時間內檢索、篩選，獲得解題的思路. 從會學習的角度看，學生就獲得了數學素養的提高.

[?] 突出數學思想和方法的教學，提倡在理解的基礎上創新

必須突出數學思想和方法的教學，使學生在把握問題、理解問題的基礎上有所創新. 要重視培養學生的觀察能力、分析能力、抽象概括能力、推理論證能力等，要加強特殊化、一般化、類比推廣、從反面考慮問題、構造法等基本數學思想方法的教學；向學生適當介紹有關創造性方法學、科學方法論等知識，啟發學生的積極思維，開闊視野. 同時，要幫助學生建立良好的數學認知結構和培養學生的廣泛遷移能力，要重視數學知識與應用的發生過程，重視知識間的有機聯系，把整體學習與局部學習有機地結合起來.

例3：在平面直角坐標系xOy中，以點（1，0）為圓心且與直線mx-y-2m-1=0（m∈R）相切的所有圓中，半徑最大的圓的標準方程為___________.

本題的切入點有兩個，一個是按部就班，找出半徑r的表達式r=，通過代數法求其最大值；另一個是將直線方程變形為m（x-2）-（y+1）=0，可“發現”直線過定點（2，-1），結合圖像，r的最大值就是點（2，-1）與圓心（1，0）之間的距離. 這種數形結合的思考就展現出了一定的思維創新，對學生學習數學和研究數學有指導意義，是學生數學核心素養的具體表現.

例4：設t∈R，若x>0時均有（tx-1）·[x2-（t+1）x-1]≥0，則實數t的值為_________.

令f（x）=tx-1，g（x）=x2-（t+1）x-1，g（x）的兩個零點x<00且f（x）的零點也為x2時不等式恒成立. 將x2=代入g（x）=0，得

t-

（t+1）=0，解得t=.

如果單純來解不等式，往往需要分類討論，中間環節對問題的理解、運算都需要較強的功底. 但是，在審題時，如果注意到不等式左邊是兩個因式相乘的形式，聯想因式對應的函數，那么對不等式就有很直觀的認識了，解法自然就會流暢很多. 在解決某些規律性較強的問題時，需要學生牢固掌握一些基本方法，形成一定的思維習慣，樹立應用數學思想方法的意識.

數學的學習不僅是指數學知識的獲得與積累，更重要的是使個體形成良好的數學認知結構，形成有序的、起作用的、有著生長點和開放面的認知結構. 數學思想方法是從操作層面上體現的數學核心素養，對培養學生的數學素養來說是一個很好的切入點，也是一個良好的機會.

[?] 優化教學過程，培養學生的主體意識

在運算教學中，要重視從激發學生學習數學的興趣入手，努力提高學生學習的積極性和主動性. 激發學生學習興趣的方式并不在于過多地求新求奇，而主要在于教學內容要在適應學生現有水平基礎上達到最近發展區水平，使教學具有啟發性. 通過挖掘數學中的美來啟迪學生的心靈，也是吸引學生自覺鉆研數學的一個重要方面.

的值.

這是一個三角計算求值的問題，試圖通過三角恒等變換達到考查運算能力的目的. 主要體現在如何選擇公式，如何確定運算方向，怎樣確定運算路徑，從合理進行運算的角度來考查運算能力.

可以引導學生分析條件和目標，從角α+與2α+之間的關系入手確定運算路徑.

關系①簡潔明朗，但在由已知求cos

2α+

的過程中，需要先求出sinα，cosα和sin

α+

的值.

關系②比關系①要復雜一些，但在求cos

2α+

的過程中，只需求出sin

，即cos2α和sin2α的值.

教師：再往下分析，由cos

α+

的值求sinα，cosα容易還是求sin2α，cos2α容易？

學生3：由于2α+=2

α+

，自然是求角2α+的正、余弦容易.

到此運算的方向基本確定.

運算能力的主要標識不在運算的本身，而是運算方向和運算路徑的確定. 來自于對問題的深刻理解，運算目標在運算過程中起到了十分重要的作用. 沒有運算目標的指引，合理的運算路徑就很難形成.

[?] 引導學生反思，提升運算品質

引導學生進行運算解題后的反思，是進一步優化數學思維品質，培養數學素養的重要舉措. 對運算的過程和結果進行評估和研判，也是學生運算能力的一種. 這一過程既是對學生運算品質的全面性培養，也是學生對自己思維活動的再認識.

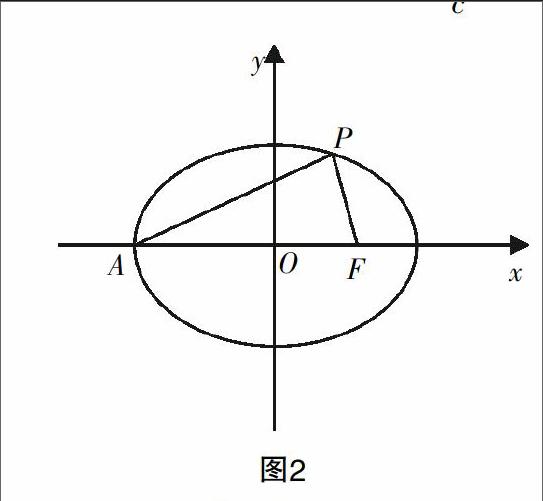
例6：如圖2，在平面直角坐標系xOy中，橢圓+=1（a>b>0）的左頂點為A，右焦點為F（c，0），P（x0，y0）為橢圓上一點，且PA⊥PF. 求證：以F為圓心，FP為半徑的圓與橢圓的右準線x=相切.

[x][O][y][P][A][F]

圖2

本題的思路不難確定，由PA⊥PF知點P（x0，y0）在以線段AF為直徑的圓上，將此圓方程與橢圓方程聯立，可解得點P的坐標；然后再求半徑FP，證明FP與點F到右準線x=的距離-c相等即可.

具體地，由PA⊥PF得·=-1，即y=-（x0+a）（x0-c）①.

又+=1②，①②聯立，如果不假思索消去y并整理成（b2-a2）x-a2（a-c）x0+a3c-a2b2=0，下一步無論用十字相乘法或是求根公式，都可能得不到理想的結果.

此時，就應引導學生對過程進行反思：解題目標是什么？思路是什么？從而促使學生再一次對兩個研究對象進行深入的觀察和思考，挖掘新特征，調整運算，達成目標.

以AF為直徑的圓與橢圓除點P這個公共點外，還有另一個公共點A，那么由①②聯立整理成關于x0的二次方程中就一定會有“x0+a”這個因子.

消y得b2x+a2[-（x0+a）（x0-c）]-a2b2=0，即b2（x-a2）=a2（x0+a）（x0-c），有（x0+a）

x0+

=0，解得x0=或x0=-a（舍去）.

課堂上，許多學生的解題思路是清楚的，目標是明確的，卻往往陷于“復雜”的運算當中不能自拔. 學生處在欲進不得、欲罷不能之時，教師引導其深挖信息，走出困境，此時學生收獲的不僅僅是解題技能的提高，更是思維水平的提升和數學學習興趣的激揚. 這樣的反思過程強化了理性思考，有效促使了學生對運算的認知理解，提高了學生自覺通過提高思維水平來達到提升運算水平的認識，數學素養也會隨之提高.

總之，高三復習過程中要把培養學生的運算能力列為明確的教學目標，輔之以相應的教學素材和教學設計. 要把學生運算能力的培養滲透到每節課、每道題中. 任何一道精心編擬的數學試題，均蘊涵著運算的通性通法或者是在數學思想方法基礎上所表現出來的合理、簡潔的運算方式. 如果注意滲透、適時講解、反復強調，貫穿于整個高三復習的始終，學生就會深入于心，形成良好的運算心理、意識和品質，數學核心素養的培養才會得到有效落實.